- Газовые законы. газовые смеси. задача 70 — задачи по химии
- Задача #13861: определите плотность смеси газов, состоящей из 8 г (условие) — студизба
- Задачи по физике
- Найти плотность ρ газовой смеси водорода и кислорода, если их массовые доли w1 и w2 равны соответственно 1/9 и 8/9. давление p смеси равно 100
- Относительная плотность по… задачи
- Относительная плотность вещества – отношение плотности вещества Б к плотности вещества А
- Примеры решенных задач по физике — контрольная 8(молекулярная физика, равновесное излучение, ядерные реакции)
- Срядняя плотность по водороду газовой смеси состоит из водорода и кислорода равна14,5.вычислите сколько объемных процентов водорода и кислорода содержится в смеси? —
Газовые законы. газовые смеси. задача 70 — задачи по химии
Средняя плотность по водороду газовой смеси состоящей из водорода и кислорода 12,5. Вычислите сколько процентов водорода и кислорода (по объему) содержит смесь.
Задача #13861: определите плотность смеси газов, состоящей из 8 г (условие) — студизба
Задачи по физике
Общий
вид уравнения колебаний:
(1)
Скорость
колебаний:
(2)
Максимальная
скорость:
(3)
В момент
когда скорость точки максимальна,
ее кинетическая энергия равна полной
энергии:
(4)
Ускорение
точки:
(5)
Максимальное
ускорение точки:
(6)
Ускорение
максимально, когда максимальна
сила, действующая на точку:
(7)
Делим
(4) на (7), получаем амплитуду колебаний:
(8)
Круговая
частота колебаний:
(9)
Подставляем
(8) и (9) в (1), получаем уравнение движения:
(м)
Ответ: .
Найти плотность ρ газовой смеси водорода и кислорода, если их массовые доли w1 и w2 равны соответственно 1/9 и 8/9. давление p смеси равно 100
готовое задание, попробуте поиск по другим похожим ключевым фразам из ее условия
| Решение задач → Задачи по физике с решениями Найти плотность ρ газовой смеси водорода и кислорода, если их массовые доли w1 и w2 равны соответственно 1/9 и 8/9. Давление p смеси равно 100 кПа, температура T=300 К.
|
Относительная плотность по… задачи
24-Фев-2022 | комментариев 26 | Лолита Окольнова
В ЕГЭ иногда встречаются задачи (часть С последнее задание), где в условии дана относительнаяплотность вещества по… водороду, кислороду, воздуху, азоту и т.д.
Например:
Относительная плотность вещества – отношение плотности вещества Б к плотности вещества А
Относительная плотность — величина безразмерная
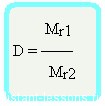
Формула достаточно простая, и из нее вытекает другая формула —
Формула молярной массы вещества
Mr1 = D•Mr2
и т.д.
В условии задачи может быть полная формулировка — «относительная плотность (паров)…», а может быть просто «плотность вещества по…»
Давайте решим нашу задачу:
Дана плотность паров вещества по воздуху, значит, нам подходит формула молярной массы вещества —
Mr (вещества)=Mr(воздуха)•D=29 гмоль • D
Mr(вещества)=29 гмоль • 1.448 = 42 гмоль
Нам дан углеводород — СхHy, значит, мы можем найти Mr(Cx и Mr(Hy). Обратите внимание, именно молярные массы, т.к.у нас несколько атомов углерода и водорода.
Для этого надо молярную массу вещества умножить на процентное содержание элемента:
Mr(Cx)=Mr(вещества)•ω
Mr(Cx)= 42 гмоль · 0.8571=36 гмоль
x=Mr(Cx)Ar(C)=36 гмоль ÷ 12 гмоль =3.
Точно так же находим все данные для водорода:
Mr(Hy)=Mr(вещества)•ω
Mr(Hy)= 42 гмоль · 0.1429=6 гмоль
x=Mr(Hy)Ar(H)=6 гмоль ÷ 1 гмоль =6.
Искомое вещество — C3H6 — пропен.
Еще раз повторим определение —
Относительная плотность газа – это сравнение молярной или относительной молекулярной массы одного газа с аналогичным показателем другого газа.
Дана относительная плотность по аргону.
Mr (вещества)=Ar(Ar)•D
Mr (CxHy)=40 гмоль ·1.05=42 гмоль
Запишем уравнение горения:
СхHy O2 = xCO2 y2H2O
Найдем количество углекислого газа и воды:
n(CO2)=V22,4 лмоль = 33.622.4=1.5
n(H2O)=mMr=2718=1.5
Соотношение х : y2 как 1.5 : 1.5, т.е. y=2x, что соответствует общей формуле алкенов: CnH2n
Выражаем в общем виде молярную массу: Mr=Mr(C) Mr(H)
12n 2n=42
n=3
Наше вещество — C3H6 — пропен
Примеры решенных задач по физике — контрольная 8(молекулярная физика, равновесное излучение, ядерные реакции)
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.
Задача 407.
Найти плотность 
газовой смеси, состоящей по массе из одной части водорода и восьми частей кислорода при давлении 
газовой смеси, состоящей по массе из одной части водорода и восьми частей кислорода при давлении и температуре
Дано : 
Найти g.
Решение. Пусть 
и 
и — масса водорода и кислорода,
и 
и — их парциальные давления,
объём смеси газов. Согласно уравнению Менделеева – Клапейрона для водорода имеем
( 1 )
а для кислорода
( 2 )
где 
— молярная масса водорода,
— молярная масса водорода, — молярная масса кислорода,
— универсальная газовая постоянная. Сложим левые и правые части уравнений (1) и (2), учитывая, что 
— универсальная газовая постоянная. Сложим левые и правые части уравнений (1) и (2), учитывая, что — давление смеси газов:
откуда объём 
Масса смеси 
поэтому её плотность
( 3 )
Пусть масса одной части составляет 
Тогда масса 
Тогда масса частей водорода
а масса 
а масса частей кислорода
Подставляем значения
и 
и в формулу (3):
Проверка размерности:
Подставляем данные:
Ответ: 
Задача 417.
Найти среднее число столкновений в 1 секунду молекул углекислого газа при температуре 
если длина свободного пробега при этих условиях равна
Дано: 
Найти 
Решение. Среднее число столкновения в единицу времени рассчитывается по формуле
( 4 )
где 
— средняя арифметическая скорость молекул, 
— средняя арифметическая скорость молекул, — средняя длина свободного пробега. В свою очередь скорость
находится по формуле
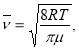( 5 )
где 
— молярная масса углекислого газа 
— молярная масса углекислого газа
Подставляем (5) в (4)
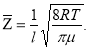
Проверка размерности:
Подставляем данные:
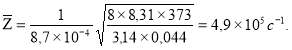
Ответ:
Задача 427.
В баллоне объёмом 
литров находится гелий под давлением 
литров находится гелий под давлением и при температуре
после того, как из баллона было взято 
после того, как из баллона было взято гелия, температура в баллоне понизилась до
Определить давление 
Определить давление гелия, оставшегося в баллоне,и изменение внутренней энергии газа.
Дано:
Найти 
Решение. Пусть 
— начальная масса гелия. Запишем уравнение Менделеева – Клапейрона
( 6 )
где 
— молярная масса гелия. После изъятия из баллона гелия массой 
— молярная масса гелия. После изъятия из баллона гелия массой его масса становится равной
и уравнение Менделеева – Клапейрона принимает вид
( 7 )
Из (6) находим массу 
и подставляем её в (7)
откуда давление 
( 8 )
Начальная внутренняя энергия гелия
а его конечная внутренняя энергия
где 
— число степеней свободы молекулы. Изменение внутренней энергии.
( 9 )
Подставляем начальную массу 
в формулу (9)
( 10 )
Проверка размерности:
Подставляем данные в формулы (8) и (10), учитывая, что гелий – одноатомный газ, поэтому имеются только три поступательные степени свободы 
Отрицательный знак 
указывает на то, что внутренняя энергия гелия уменьшается.
Ответ: 
Задача 437.
Азот массой 
адиабатически расширили в
а затем изобарно сжали до первоначального объёма. Определить изменение энтропии DS газа в ходе указанных процессов.
Дано: 
Найти 
Решение. Процессы, в которых участвует газ, изображены на рис.1 на
— диаграмме.
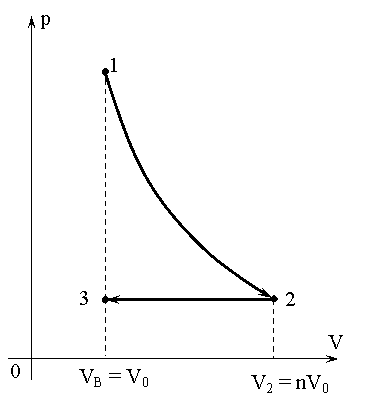
Процесс 1-2 представляет собой адиабатическое расширение, а процесс 2-3 – изобарное сжатие. Изменение энтропии в этих процессах
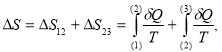( 11 )
где 
— подводимое к газу количество теплоты. При адиабатическом процессе газ теплоизолирован и 
— подводимое к газу количество теплоты. При адиабатическом процессе газ теплоизолирован и Поэтому в данном процессе энтропия не изменяется:
При изобарном процессе при изменении температуры на малое значение
( 12 )
где 
— молярная теплоёмкость при постоянном давлении. Подставляем (12) в (11), получаем
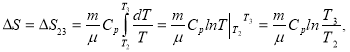( 13 )
где 
температура газа в состояниях 2 и 3. При изобарном процессе
поэтому
( 14 )
( см.рис.1). Молярная теплоёмкость при постоянном давлении
( 15 )
При этом число степеней свободы для двухатомной молекулы азота 
Подставляя (14) и (15) в ( 13), окончательно получаем
Проверка размерности:
Подставляем данные:
Видно, что энтропия при переходе газа из состояния 1 в состояние 3 уменьшается.
Ответ: 
Задача 447.
За 5 мин. излучается энергия 
Площадь окошка 
Площадь окошка Принимая, что окошко излучает как абсолютно чёрное тело, определить температуру печи.
Дано: 
Найти 
Решение. Излучаемая энергия равна
( 16 )
где 
энергетическая светимость, 
энергетическая светимость, — площадь излучателя,
промежуток времени. Согласно закону Стефана – Больцмана энергетическая светимость абсолютно черного тела
( 17 )
где 
— постоянная Стефана- Больцмана, 
— постоянная Стефана- Больцмана, — температура. Подставляем (17)в (16)
откуда находим температуру 
Проверка размерности:
Подставляем данные:
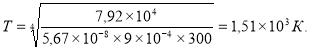
Ответ: 
Задача 457.
В одном акте деления ядра урана 
освобождается энергия 
освобождается энергия Определить: 1) энергию, выделяющуюся при распаде всех ядер этого изотопа урана массой
2) массу каменного угля с удельной теплотой сгорания
эквивалентную в тепловом отношении 
эквивалентную в тепловом отношении урана
Дано: 
Найти 
Решение. Если в одном анте деления выделяется энергия 
то при распаде 
то при распаде ядер выделяется энергия
Рассчитаем количество ядер 
в уране массой 
в уране массой Количество урана
где 
где — молярная масса изотопа
Поэтому
где 
постоянная Авогадро. Таким образом, выделяемая энергия
Эквивалентная в тепловом отношении масса каменного угля
Проверка размерности:
Подставляем данные, предварительно переведя энергию 
из
из в
Ответ: 1) 
2) 2,8 тысячи тонн.
Срядняя плотность по водороду газовой смеси состоит из водорода и кислорода равна14,5.вычислите сколько объемных процентов водорода и кислорода содержится в смеси? —
обозначим объемную долю водорода за х, тогда получим уравнение
два икс плюс 32(1-х) равно 29, раскрываем скобки и находим х=о,1. Объемная доля водорода 10 процентов, а кислорода 90 процентов