Число степеней свободы молекул газа
В термодинамике под степенями свободы понимают не зависимые термодинамические параметры, определяющие состояние термодинамического равновесия системы. Молекулы газа постоянно находятся в состоянии теплового хаотического движения, совершая при этом поступательное движение, вращательное и колебательное. Так при соударениях молекул многоатомных газов возникает их вращение вокруг центров масс.
Атомы в молекулах могут совершать колебания относительно среднего положения равновесия. Экспериментально доказано, что колебания атомов в молекулах происходят при температурах, превышающих 200 — 250°С. Для учёта всех видов механических движений и энергий вводится понятие числа степеней свободы молекулы.
Числом степеней свободы i молекулы (любого тела) называется число независимых координат, определяющих положение молекулы (тела) в пространстве при её движении.
Молекулу одноатомного газа, согласно модели идеального газа, можно представить, как материальной точки. Положение материальной точки в пространстве определяется тремя независимыми координатами х, у, z.
Следовательно, такая молекула имеет три степени свободы (г = 3) поступательного движения. Вращательное движение материальной точки вокруг оси, проходящей через неё, рассматривать не имеет физического смысла. Момент инерции J молекулы относительно оси, проходящей через неё, равен нулю и кинетическая энергия вращательного движения равна нулю (J = т ? г 2 —> О
и Wepau,=
2
Молекулу двухатомного газа можно рассматривать, как совокупность двух материальных точек (атомов), жестко связанных между собой молекулярными силами. Положение молекулы в пространстве описывают пять координат: три координаты х, у, z центра масс О и два угла, определяющие направление оси в пространстве, т.е. прямой, проходящей через атомы (рис.48 а, б).
Итак, молекула двухатомного газа имеет пять степеней свободы (г = 5), из них три поступательные степени свободы (г„ос = 3) и две вращательные степени свободы (iep = 2), соответствующие вращению молекулы вокруг двух взаимно перпендикулярных осей O ‘O ‘ и О’О»,
проходящих через центр масс О. Вращение вокруг оси 00, совпадающей с прямой, соединяющей атомы, не имеет физического смысла, так как положение молекулы в пространстве не изменяется.
Атомы в двухатомной молекуле могут быть не жёстко связанными между собой. Например, расстояние между атомами изменяется за счёт колебаний их относительно друг друга.

Рис.48 б)
Положение в пространстве двухатомной молекулы с упругой связью между атомами определяется шестью координатами — тремя координатами центра масс, двумя координатами поворота осей (как и у двухатомной молекулы с жёсткой связью) и расстоянием между атомами. Вращение вокруг оси ОО, совпадающей с прямой, соединяющей атомы, не имеет физического смысла, так как положение молекулы в пространстве не изменяется.
Атомы в двухатомной молекуле могут быть не жёстко связанными между собой. Например, расстояние между атомами изменяется за счёт колебаний их относительно друг друга. Положение в пространстве двухатомной молекулы с упругой связью между атомами определяется шестью координатами — тремя координатами центра масс, двумя координатами поворота осей (как и у двухатомной молекулы с жёсткой связью) и расстоянием между атомами.
Двухатомная молекула с упругой связью имеет шесть степеней свободы (г =6), из них три степени поступательные (г пос = 3), две вращательные (г вр = 2) и одна колебательная (г кол = 1).
Трёхатомная молекула и многоатомные молекулы с жёсткой связью имеют шесть степеней свободы (г = 6) — три поступательные (i пос = 3) и три вращательные (г ер = 3).
При высоких температура (t > 200 °С) число степеней свободы молекул увеличивается за счёт колебательного движения.
Число степеней свободы молекулы. закон равномерного распределения энергии по степеням свободы.
В механике введилось понятие числа степеней свободы: это число независимых переменных (координат), которые полностью определяют положение системы в пространстве. В некоторых задачах молекулу одноатомного газа (рис. 1, а) рассматривают как материальную точку, которой задают три степени свободы поступательного движения. При этом не учитывается энергия вращательного движения.
В механике молекула двухатомного газа в первом приближении считается совокупностью двух материальных точек, которые жестко связанны недеформируемой связью (рис. 1, б). Данная система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Вращение вокруг третьей оси, проходящей через оба атома, лишено смысла. Значит, у двухатомного газа пять степеней свободы (i = 5). У трехатомной (рис. 1, в) и многоатомной нелинейной молекулы шесть степеней свободы: три поступательных и три вращательных. Естественно считать, что жесткой связи между атомами не существует. Поэтому необходимо учитывать для реальных молекул также степени свободы колебательного движения.
Рис.1 
При любом числе степеней свободы данной молекулы три степени свободы всегда поступательные. Ни одна из поступательных степеней свободы не имеет преимущества перед другими, значит на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения <ε0> (энергия поступательного движения молекул):
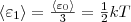
В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекулы
где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы: i=iпост iвращ 2iколеб
В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы.
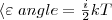
Так как в идеальном газе взаимная потенциальная энергия взаимодействия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия для одного моля газа, будет равна сумме кинетических энергий NA молекул:
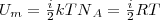 (1)
(1)
Внутренняя энергия для произвольной массы m газа.

где М — молярная масса, ν — количество вещества.
Число степеней свободы тела — это сколько координат надо знать, чтобы отнгозначно описать его движение. Например, для материальной точки (имеющей нулевой размер) достаточно знать три параметра — по осям коголрдинат.
В молекулярно-кинетической теории газов, помимо трех поступательных степеней свободы, есть и вращательные, число которых зависит от строения молекулы газа. Например, для кислорода или азота (молекула из двух атомов) надо рассматривать вращение вокруг двух осей (потому что вокруг третьей — это вдоль молекулы, и там нет изменения положения никакого). Для более сложных, например, аммиак, появляются все три дополнительные вращательные степени свободы. Поэтому и энергия молекул должна считаться как, например, 5/2 kT для кислорода или 3kT для аммиака, потому как полное число степеней свободы 5 и 6, соответственно. А вот гелий или неон — одноатомные газы, и для них только 3/2kT, посколку нет вращательных степеней свободы.
Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы.
Внутренняя энергияU — энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т.д.) и энергия взаимодействия этих частиц. К внутренней энергии не относится кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях.Внутренняя энергия -однозначная функция термодинамического состояния системы, т.е. в каждом состоянии система обладает вполне определенной (единственной) энергией. Внутренняя энергия не зависит от того, как система пришла в данное состояние: при переходе из состояния (1) в состояние (2) изменение внутренней энергии DU определяется только разностью значений внутренней энергии этих состояний DU = U1 — U2 и не зависит от пути перехода.
Число степеней свободы системыi — это число независимых переменных (координат), полностью определяющих положение системы в пространстве:
— Одноатомная молекула идеального газа имеет три степени свободы поступательного движения, т.е. i=3.
— Двухатомная молекула идеального газа имеет три степени поступательного движения и две степени свободы вращательного движения, т.е. i=5.
— Трехатомная молекула (и вообще нелинейная многоатомная молекула) идеального газа имеет три степени поступательного движения и три степени вращательного движения, т.е. i=6.
— Для реальных молекул следует учитывать также степени свободы колебательного движения.
— Независимо от числа степеней свободы молекул три степени свободы всегда поступательные; ни одна из поступательных степеней свободы не имеет преимущества перед остальными.
Закон Больцмана о равномерном распределении энергии по степеням свободы молекул:
для системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень — в среднем энергия, равная kT (на колебательную степень свободы приходится не только кинетическая энергия, но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы). Таким образом, средняя энергия молекулыЕ> = ikT/2, где i — сумма числа поступательных iпост, числа вращательных iвращ и удвоенного числа колебательных iколеб степеней свободы молекулы i = iпост iвращ 2iколеб. Для идеального газа i совпадает с числом степеней свободы молекулы.
Внутренняя энергия 1 моль идеального газа равна сумме кинетических энергий NAмолекул
Um = ikTNA = iRT/2, (1a)
и изменение внутренней энергии 1 моль идеального газа dUm =(iR/2)dT (1b)
(молекулы между собой не взаимодействуют и поэтому взаимная потенциальная энергия молекул газа равна нулю).
Внутренняя энергия произвольной массы m идеального газа U = (m/M)(iRT/2)=n(iRT/2), где М — молярная масса (масса одного моля), n = m/M — количество вещества.
§
Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус:
Размерность теплоемкости: [C] = Дж/К.
Однако, теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости.
Удельная теплоёмкость (Суд) есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [Cуд] = Дж/К.
Для газов удобно пользоваться молярной теплоемкостью Cμ— количество теплоты, необходимое для нагревания 1 моля газа на 1 градус:
[Cμ] = Дж/(моль*К).
Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании.
Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается СV.
СР – теплоемкость при постоянном давлении. Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу
Следовательно, проводимое тепло затрачивается и на нагревание и на совершение работы. Отсюда ясно, что 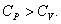 .
.
Теплоемкость при постоянном объёме будет равна:
При изобарическом процессе, кроме увеличения внутренней энергии, происходит совершение работы газом:
Из основного уравнения молекулярно-кинетической теории 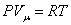 . При изобарическом процессе Р = const. Следовательно, получим:
. При изобарическом процессе Р = const. Следовательно, получим:
Это уравнение Майера для одного моля газа.
Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе.
Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж.
Полезно знать формулу Майера для удельных теплоёмкостей:
или
Второе начало термодинамики. Энтропия.Статистическое толкование энтропии. Связь с термодинамической вероятностью.
Самопроизвольный процесс– процесс, который может протекать без затраты работы извне. Самопроизвольный процесс может протекать или обратимо, или необратимо.
Вынужденный процесс – процесс, для протекания которого требуется затрата работы извне в количестве, пропорциональном производимому изменению состояния системы.
Второе начало термодинамики дает возможность определить, какой из процессов будет протекать самопроизвольно, какое количество работы может быть при этом получено, каков предел самопроизвольного течения процесса. Далее, второе начало термодинамики дает возможность определить, какими должны быть условия, чтобы нужный процесс протекал в необходимом направлении и в требуемой степени, что особенно важно для решения различных задач прикладного характера. Применимо лишь к макроскопическим системам.
Формулировки второго начала термодинамики:
— Теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому (постулат Клаузиуса).
— Невозможен процесс, единственным результатом которого является превращение теплоты в работу.
— Невозможно построить машину, все действия которой сводились бы к производству работы за счет охлаждения теплового источника (вечный двигатель второго рода).
Величина связанной энергии тем больше, чем меньше разность температур, и при T = const тепловая машина не может производить работу. Мерой связанной энергии является новая термодинамическая функция состояния, называемая энтропией.
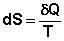 — выражение является определением новой функции состояния – энтропии и математической записью второго начала термодинамики для обратимых процессов.
— выражение является определением новой функции состояния – энтропии и математической записью второго начала термодинамики для обратимых процессов.
Если система обратимо переходит из состояния 1 в состояние 2, изменение энтропии будет равно:

Для необратимых процессов можно записать неравенства:
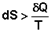
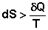

1) В изолированных системах самопроизвольно могут протекать только процессы, сопровождающиеся увеличением энтропии.
2) Энтропия изолированной системы не может самопроизвольно убывать.
Оба этих вывода также являются формулировками второго начала термодинамики.
§
С точки зрения статистической термодинамики второе начало термодинамики можно сформулировать следующим образом:
Система стремится самопроизвольно перейти в состояние с максимальной термодинамической вероятностью.
Статистическое толкование второго начала термодинамики придает энтропии конкретный физический смысл меры термодинамической вероятности состояния системы.
Больцманом в теорию теплоты были введены статистические представления. Каждому состоянию системы приписывается термодинамическая вероятность (определяемая как число микросостояний, составляющих данное макросостояние системы), тем большая, чем более неупорядоченным или неопределенным является это состояние. Т.о., энтропия есть функция состояния, описывающая степень неупорядоченности системы. Количественная связь между энтропией S и термодинамической вероятностью W выражается формулой Больцмана: 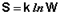
Круговой процесс. Обратимые и необратимые процессы. Тепловые двигатели. Холодильные машины. Цикл Карно и его КПД для идеального газа.
Круговым процессом (или циклом) называется процесс, при котором система, проходя через ряд состояний, возвращается в первоначальное.
Если за цикл совершается положительная работа A=∫pdV>0 (цикл идет по часовой стрелке), то он называется прямым.
Если за цикл осуществляется отрицательная работа A=∫pdV<0 (цикл идет против часовой стрелки), то он называется обратным.
Прямой цикл применяется в тепловых двигателях — периодически действующих двигателях, которые совершают работу за счет полученной извне теплоты. Обратный цикл применяется в холодильных машинах — периодически действующих установках, в которых за счет работы внешних сил теплота переходит к телу с более высокой температурой.
Первое начало термодинамики для кругового процесса:
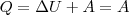
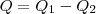
где Q1 — количество теплоты, которая получила система, Q2 — количество теплоты, которое отдала система.
Термический коэффициент полезного действия для кругового процесса:
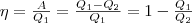
Термодинамический процесс называется обратимым, если он может осуществляться как в прямом, так и в обратном направлении, причем если такой процесс осуществляется сначала в прямом, а затем в обратном направлении и система возвращается в первоначальное состояние, то в окружающей среда и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.
Цикл Карно
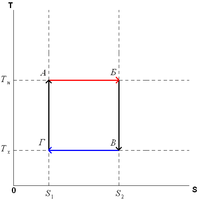
Цикл Карно состоит из четырёх стадий:
1. Изотермическое расширение (на рисунке — процесс A>Б). В начале процесса рабочее тело имеет температуру TH, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты QH. При этом объём рабочего тела увеличивается.
2. Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс Б>В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.
3. Изотермическое сжатие (на рисунке — процесс В>Г). Рабочее тело, имеющее к тому времени температуру TX, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты QX.
4. Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс Г>А). Рабочее тело отсоединяется от холодильника . При этом его температура увеличивается до температуры нагревателя.
Цикл Карно
КПД цикла Карно:
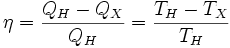
Отсюда видно, что КПД цикла Карно с идеальным газом зависит только от температуры награвателя (Tн) и холодильника (Тх).
Из уравнения следуют выводы:
1. Для повышения КПД тепловой машины нужно увеличить температуру нагревателя и уменьшить температуру холодильника;
2. КПД тепловой машины всегда меньше 1.
Цикл Карно обратим, так как все его составные части являются равновесными процессами.
§
Для реальных газов необходимо ввести поправки в уравнение состояния идеального газа, учитывающие объем молекул и силы их взаимодействия. Эти поправки были учтены голландским физиком Ван-дер-Ваальсом. Часть объема V газа занята самими молекулами. Поэтому объем, занимаемый газом, должен быть уменьшен на величину b, пропорциональную объему молекул:
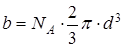 , (1)
, (1)
где 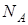 – постоянная Авогадро,
– постоянная Авогадро, 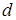 – диаметр молекулы. Теоретические расчёты показывают, что величина b в четыре раза превосходит объем молекул.
– диаметр молекулы. Теоретические расчёты показывают, что величина b в четыре раза превосходит объем молекул.
В реальных газах имеются силы взаимного притяжения молекул, которые действуют дополнительно к силам внешнего давления и как бы сжимают газ. Вследствие этого возникает добавочное внутреннее давление  , которое пропорционально квадрату концентрации молекул или обратно пропорционально квадрату объема газа:
, которое пропорционально квадрату концентрации молекул или обратно пропорционально квадрату объема газа:
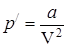 , (2)
, (2)
где
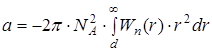 , (3)
, (3)
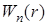 – потенциальная энергия притяжения двух молекул (
– потенциальная энергия притяжения двух молекул ( 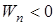 ).
).
Принимая данные обстоятельства во внимание, уравнение состояния реального газа принимает следующий вид:
 , (4)
, (4)
где а,  – константы, определяемые экспериментальным путём,
– константы, определяемые экспериментальным путём, 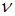 –количество вещества,
–количество вещества, 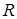 – универсальная газовая постоянная.
– универсальная газовая постоянная.
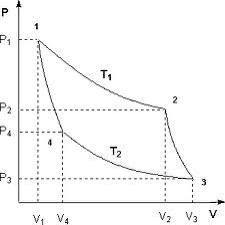
Изотермы
Исследование уравнения (4) удобно производить, рассматривая изотермы Ван-дер-Ваальса. Анализируя графики 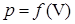 на рис. 1, можно сделать три вывода.
на рис. 1, можно сделать три вывода.
1. При высоких температурах (например, T1, которой соответствует изотерма 1) изобара AD пересекает изотерму в одной точке. Уравнение Ван-дер-Ваальса имеет один вещественный корень, т.е. каждому значению T соответствует единственное значение объема. Из этого следует, что при высоких температурах вещество находится в однофазном – газообразном состоянии.
2. Невысоким температурам соответствуют изотермы 2, 3, 4, на которых имеются перегибы. Изобара AD пересекает изотерму 4 в трех точках А, B, C. В уравнении Ван-дер-Ваальса это состояние соответствует трём вещественным значениям объема при данных p и T. Это означает, что вещество находится в трёх фазовых состояниях. Под фазойпонимают совокупность всех частей системы, обладающих одинаковыми физическими и химическими свойствами.
3. Переход изотермы 5 к изотермам 4, 3 и т. д., соответствующий повышению температуры, приводит к тому, что изгибы на изотермах сглаживаются. Расстояние, например, между точками A и C уменьшается и уже на изотерме 2 они сливаются в одну точку – точку К перегиба. В точке перегиба изобара 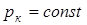 является касательной к изотерме. Температура Tк, соответствующая этой изотерме называется критической температурой.
является касательной к изотерме. Температура Tк, соответствующая этой изотерме называется критической температурой.
Экспериментальные изотермы (рис. 2) могут быть получены путём сжатия газа в изотермических условиях. Экспериментальные и теоретические изотермы на участках 1 – 2 и 3 – 4 с известным приближением можно считать совпадающими. При особых условиях эксперимента могут быть получены участок 2 – 2/, соответствующий пересыщенному пару, и участок 3 – 3/, относящийся к перегретой жидкости. Это малоустойчивые, метастабильные состояния.
Метастабильным состоянием называется равновесное состояние с ограниченной устойчивостью. При отклонении от этого состояния вещество не стремится к нему обратно, а легко переходит в другое устойчивое состояние. Метастабильные состояния существуют ограниченное время. Чтобы получить такое метастабильное состояние как перегретый пар необходимо отсутствие в газе инородных и смачиваемых включений, которые являются центрами конденсации. Перегретой может быть только очень чистая жидкость, в которой нет зародышей газовой фазы. Как правило, они всегда присутствуют в виде мельчайших пузырьков на стенках сосуда, содержащего жидкость, или на взвешенных в жидкости пылинках.
Вещество на участке 2 – 3 находиться в двухфазном состоянии, т. е. часть первоначального газообразного вещества превратилась в жидкость, а часть осталась в газообразном состоянии. Соответствующее участку 2 – 3 давление называется давлением насыщения. Точка 3 (рис. 2) соответствует состоянию, когда весь газ превращается в жидкость.
С ростом температуры участки, соответствующие двухфазному состоянию, становятся уже (рис. 3). Затем появляется изотерма, на которой этот участок превращается в точку перегиба К; ей соответствует критическая температура. При температурах ниже критической есть участок насыщения, и вещество может переходить из газообразного состояния в жидкое состояние (область I, рис. 3). Температурам выше критической соответствует только газообразное состояние (область II, рис. 3). Область III, примыкающая к оси ординат (рис. 3), относится к жидкому состоянию системы.
Критическая температура – это наивысшая температура, при которой газ может ещё быть превращён в жидкость. Давление и объем, соответствующие точке перегиба К, называются критическими. При критическом состоянии вещества различия в свойствах пара и жидкости отсутствуют. Критическое состояние характеризуется непрерывным переходом пара в жидкость и жидкости в пар. При этом удельная теплота парообразования и коэффициент поверхностного натяжения равны нулю. Параметры критического состояния вещества связаны с постоянными Ван-дер-Ваальса 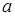 и
и  :
:
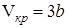 ,
, 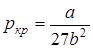 ,
,  , (5)
, (5)
или
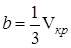 ,
, 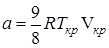 .
.
§
Физические свойства жидкостей
Текучесть
Основным свойством жидкостей является текучесть. Если к участку жидкости, находящейся в равновесии, приложить внешнюю силу, то возникает поток частиц жидкости в том направлении, в котором эта сила приложена: жидкость течёт. Таким образом, под действием неуравновешенных внешних сил жидкость не сохраняет форму и относительное расположение частей, и поэтому принимает форму сосуда, в котором находится.
В отличие от пластичных твёрдых тел, жидкость не имеет предела текучести: достаточно приложить сколь угодно малую внешнюю силу, чтобы жидкость потекла.
Сохранение объёма
Одним из характерных свойств жидкости является то, что она имеет определённый объём (при неизменных внешних условиях). Жидкость чрезвычайно трудно сжать механически, поскольку, в отличие от газа, между молекулами очень мало свободного пространства. Давление, производимое на жидкость, заключенную в сосуд, передаётся без изменения в каждую точку объёма этой жидкости (закон Паскаля, справедлив также и для газов). Эта особенность, наряду с очень малой сжимаемостью, используется в гидравлических машинах.
Жидкости обычно увеличивают объём (расширяются) при нагревании и уменьшают объём (сжимаются) при охлаждении. Впрочем, встречаются и исключения, например, вода сжимается при нагревании, при нормальном давлении и температуре от 0 °C до приблизительно 4 °C.
Вязкость
Кроме того, жидкости (как и газы) характеризуются вязкостью. Она определяется как способность оказывать сопротивление перемещению одной из частей относительно другой — то есть как внутреннее трение.
Когда соседние слои жидкости движутся относительно друг друга, неизбежно происходит столкновение молекул дополнительно к тому, которое обусловлено тепловым движением. Возникают силы, затормаживающие упорядоченное движение. При этом кинетическая энергия упорядоченного движения переходит в тепловую — энергию хаотического движения молекул.
Жидкость в сосуде, приведённая в движение и предоставленная самой себе, постепенно остановится, но её температура повысится.
Образование свободной поверхности и поверхностное натяжение
Из-за сохранения объёма жидкость способна образовывать свободную поверхность. Такая поверхность является поверхностью раздела фаз данного вещества: по одну сторону находится жидкая фаза, по другую — газообразная (пар), и, возможно, другие газы, например, воздух.
Если жидкая и газообразная фазы одного и того же вещества соприкасаются, возникают силы, которые стремятся уменьшить площадь поверхности раздела — силы поверхностного натяжения. Поверхность раздела ведёт себя как упругая мембрана, которая стремится стянуться.
Поверхностное натяжение может быть объяснено притяжением между молекулами жидкости. Каждая молекула притягивает другие молекулы, стремится «окружить» себя ими, а значит, уйти с поверхности. Соответственно, поверхность стремится уменьшиться.
Поэтому мыльные пузыри и пузыри при кипении стремятся принять сферическую форму: при данном объёме минимальной поверхностью обладает шар. Если на жидкость действуют только силы поверхностного натяжения, она обязательно примет сферическую форму — например, капли воды в невесомости.
Маленькие объекты с плотностью, большей плотности жидкости, способны «плавать» на поверхности жидкости, так как сила тяготения меньше силы, препятствующей увеличению площади поверхности.
Испарение и конденсация
Испарение — постепенный переход вещества из жидкости в газообразную фазу (пар).
При тепловом движении некоторые молекулы покидают жидкость через её поверхность и переходят в пар. Вместе с тем, часть молекул переходит обратно из пара в жидкость. Если из жидкости уходит больше молекул, чем приходит, то имеет место испарение.
Конденсация — обратный процесс, переход вещества из газообразного состояния в жидкое. При этом в жидкость переходит из пара больше молекул, чем в пар из жидкости.
Испарение и конденсация — неравновесные процессы, они происходят до тех пор, пока не установится локальное равновесие (если установится), причём жидкость может полностью испариться, или же прийти в равновесие со своим паром, когда из жидкости выходит столько же молекул, сколько возвращается.
Кипение
Кипение — процесс парообразования внутри жидкости. При достаточно высокой температуре давление пара становится выше давления внутри жидкости, и там начинают образовываться пузырьки пара, которые (в условиях земного притяжения) всплывают наверх.
Смачивание
Смачивание — поверхностное явление, возникающее при контакте жидкости с твёрдой поверхностью в присутствии пара, то есть на границах раздела трёх фаз.
Смачивание характеризует «прилипание» жидкости к поверхности и растекание по ней (или, наоборот, отталкивание и нерастекание). Различают три случая: несмачивание, ограниченное смачивание и полное смачивание. Смачивание бывает двух видов:
Иммерсионное (вся поверхность твёрдого тела контактирует с жидкостью)
Контактное (состоит из трёх фаз — твердая, жидкая, газообразная)
Смачивание зависит от соотношения между силами сцепления молекул жидкости с молекулами (или атомами) смачиваемого тела (адгезия) и силами взаимного сцепления молекул жидкости (когезия).
Если жидкость контактирует с твёрдым телом, то существуют две возможности:
молекулы жидкости притягиваются друг к другу сильнее, чем к молекулам твёрдого тела. В результате силы притяжения между молекулами жидкости собирают её в капельку. Так ведёт себя ртуть на стекле, вода на парафине или «жирной» поверхности. В этом случае говорят, что жидкость не смачивает поверхность;
молекулы жидкости притягиваются друг к другу слабее, чем к молекулам твёрдого тела. В результате жидкость стремится прижаться к поверхности, расплывается по ней. Так ведёт себя ртуть на цинковой пластине, вода на чистом стекле или дереве. В этом случае говорят, что жидкость смачивает поверхность.
Смешиваемость
Смешиваемость — способность жидкостей растворяться друг в друге. Пример смешиваемых жидкостей: вода и этиловый спирт, пример несмешиваемых: вода и жидкое масло.
Диффузия
При нахождении в сосуде двух смешиваемых жидкостей молекулы в результате теплового движения начинают постепенно проходить через поверхность раздела, и таким образом жидкости постепенно смешиваются. Это явление называется диффузией (происходит также и в веществах, находящихся в других агрегатных состояниях).
Перегрев и переохлаждение
Жидкость можно нагреть выше точки кипения таким образом, что кипения не происходит. Для этого необходим равномерный нагрев, без значительных перепадов температуры в пределах объёма и без механических воздействий, таких, как вибрация. Если в перегретую жидкость бросить что-либо, она мгновенно вскипает. Перегретую воду легко получить в микроволновой печи.
Переохлаждение — охлаждение жидкости ниже точки замерзания без превращения в твёрдое агрегатное состояние. Как и для перегрева, для переохлаждения необходимо отсутствие вибрации и значительных перепадов температуры.
Волны плотности
Хотя жидкость чрезвычайно трудно сжать, тем не менее, при изменении давления её объем и плотность всё же меняются. Это происходит не мгновенно; так, если сжимается один участок, то на другие участки такое сжатие передаётся с запаздыванием. Это означает, что внутри жидкости способны распространяться упругие волны, более конкретно, волны плотности. Вместе с плотностью меняются и другие физические величины, например, температура.
Если при распространении волны́ плотность меняется достаточно слабо, такая волна называется звуковой волной, или звуком.
Если плотность меняется достаточно сильно, то такая волна называется ударной волной. Ударная волна описывается другими уравнениями.
Волны плотности в жидкости являются продольными, то есть плотность меняется вдоль направления распространения волны. Поперечные упругие волны в жидкости отсутствуют из-за несохранения формы.
Упругие волны в жидкости со временем затухают, их энергия постепенно переходит в тепловую энергию. Причины затухания — вязкость, «классическое поглощение», молекулярная релаксация и другие. При этом работает так называемая вторая, или объёмная вязкость — внутреннее трение при изменении плотности. Ударная волна в результате затухания через какое-то время переходит в звуковую.
Упругие волны в жидкости подвержены также рассеянию на неоднородностях, возникающих в результате хаотического теплового движения молекул.
Волны на поверхности
Если сместить участок поверхность жидкости от положения равновесия, то под действием возвращающих сил поверхность начинает двигаться обратно к равновесному положению. Это движение, однако, не останавливается, а превращается в колебательное движение около равновесного положения и распространяется на другие участки. Так возникают волны на поверхности жидкости.
Если возвращающая сила — это преимущественно силы тяжести, то такие волны называются гравитационными волнами (не путать с волнами гравитации). Гравитационные волны на воде можно видеть повсеместно.
Если возвращающая сила — это преимущественно сила поверхностного натяжения, то такие волны называются капиллярными.
Если эти силы сопоставимы, такие волны называются капиллярно-гравитационными.
Волны на поверхности жидкости затухают под действием вязкости и других факторов.
Сосуществование с другими фазами
Формально говоря, для равновесного сосуществования жидкой фазы с другими фазами того же вещества — газообразной или кристаллической — нужны строго определённые условия. Так, при данном давлении нужна строго определённая температура. Тем не менее, в природе и в технике повсеместно жидкость сосуществует с паром, или также и с твёрдым агрегатным состоянием — например, вода с водяным паром и часто со льдом (если считать пар отдельной фазой, присутствующей наряду с воздухом). Это объясняется следующими причинами.
— Неравновесное состояние. Для испарения жидкости нужно время, пока жидкость не испарилась полностью, она сосуществует с паром. В природе постоянно происходит испарение воды, также как и обратный процесс — конденсация.
— Замкнутый объём. Жидкость в закрытом сосуде начинает испаряться, но поскольку объём ограничен, давление пара повышается, он становится насыщенным ещё до полного испарения жидкости, если её количество было достаточно велико. При достижении состояния насыщения количество испаряемой жидкости равно количеству конденсируемой жидкости, система приходит в равновесие. Таким образом, в ограниченном объёме могут установиться условия, необходимые для равновесного сосуществования жидкости и пара.
— Присутствие атмосферы в условиях земной гравитации. На жидкость действует атмосферное давление (воздух и пар), тогда как для пара должно учитываться практически только его парциальное давление. Поэтому жидкости и пару над её поверхностью соответствуют разные точки на фазовой диаграмме, в области существования жидкой фазы и в области существования газообразной соответственно. Это не отменяет испарения, но на испарение нужно время, в течение которого обе фазы сосуществуют. Без этого условия жидкости вскипали бы и испарялись очень быстро.
капиллярный эффект — физическое явление, заключающееся в способности жидкостей изменять уровень в трубках, узких каналах произвольной формы, пористых телах. В поле тяжести (или сил инерции, например при центрифугировании пористых образцов) поднятие жидкости происходит в случаях смачивания каналов жидкостями, например воды в стеклянных трубках, песке, грунте и т. п. Понижение жидкости происходит в трубках и каналах, не смачиваемых жидкостью, например ртуть в стеклянной трубке.
§
Электрическое поле.Для объяснения природы электрических взаимодействий заряженных тел необходимо допустить наличие в окружающем заряды пространстве физического агента, осуществляющего это взаимодействие. В соответствии с теорией близкодействия, утверждающей, что силовые взаимодействия между телами осуществляются через посредство особой материальной среды, окружающей взаимодействующие тела и передающей любые изменения таких взаимодействий в пространстве с конечной скоростью, таким агентом является электрическое поле.
Электрическое поле создается как неподвижными, так и движущимися зарядами. О наличии электрического поля можно судить, прежде всего, по его способности оказывать силовое действие на электрические заряды, движущиеся и неподвижные, а также по способности индуцировать электрические заряды на поверхности проводящих нейтральных тел.
Поле, создаваемое неподвижными электрическими зарядами, называют стационарным электрическим, или электростатическим полем. Оно представляет собой частный случай электромагнитного поля, посредством которого осуществляются силовые взаимодействия между электрически заряженными телами, движущимся в общем случае произвольным образом относительно системы отсчета.
Напряженность электрического поля.Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E, называемая напряжённостью электрического поля.
E= F / qпр.
Она определяется отношением силы F, действующей со стороны поля на точечный пробный заряд qпр, помещенный в рассматриваемую точку поля, к величине этого заряда.
Понятие «пробный заряд» предполагает, что этот заряд не участвует в создании электрического поля и так мал, что не искажает его, т. е. не вызывает перераспределения в пространстве зарядов, создающих рассматриваемое поле. В системе СИ единицей напряженности служит 1 В / м, что эквивалентно 1 Н / Кл.
Напряженность поля точечного заряда.Используя закон Кулона (1.1) найдем выражение для напряжённости электрического поля, создаваемого точечным зарядом q в однородной изотропной среде на расстоянии r от заряда:
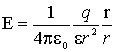
 (1.2)
(1.2)
В этой формуле r – радиус-вектор, соединяющий заряды q и qпр. Из (1.2) следует, что напряжённость E поля точечного заряда q во всех точках поля направлена радиально от заряда при q > 0 и к заряду при q < 0.
Графическое изображение электрического поля.Метод графического изображения электрического поля был предложен английским физиком Майклом Фарадеем. Суть метода заключается в том, что на чертеже изображаются непрерывные линии, которые называют линиями напряженности, или силовыми линиями.
Правило построения линий напряженности заключается в том, что касательные к ним в каждой точке чертежа совпадают с направлением вектора напряженности поля в изображаемой точке.
Таким образом, силовые линии имеют то же направление, что и напряжённость поля и не пересекаются, так как в каждой точке электрического поля вектор E имеет лишь одно направление.
С помощью силовых линий можно дать количественную характеристику напряжённости электрического поля. Для этого густота, или плотность, силовых линий выбирается пропорционально модулю вектора напряженности. Плотность силовых линий определяется как число линий, пронизывающих единичную поверхность в направлении, перпендикулярном к этой поверхности.
Изображение силовых линий позволяет получать картину поля, которая наглядно показывает, чему равна напряженность в разных частях поля и как она изменяется в пространстве.
Если поле образовано не одним зарядом, а несколькими, то силы, действующие на пробный заряд, складываются по правилу сложения векторов. Поэтому и напряженность системы зарядов в данной точке, поля равна векторной сумме напряженностей полей от каждого заряда в отдельности.
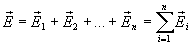
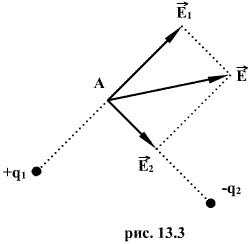
Согласно принципу суперпозиции электрических полей можно найти напряженность в любой точке А поля двух точечных зарядов  и
и  (рис. 13.1). Сложение векторов
(рис. 13.1). Сложение векторов  и
и  производится по правилу параллелограмма. Направление результирующего вектора
производится по правилу параллелограмма. Направление результирующего вектора  находится построением, а его абсолютная величина может быть подсчитана по формуле
находится построением, а его абсолютная величина может быть подсчитана по формуле
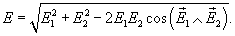
Итак, на примерах мы показали, что, если силовые линии однородного электрического поля напряженностью  пронизывают некоторую площадку S, то поток вектора напряженности (раньше мы называли число силовых линий через площадку) будет определяться формулой:
пронизывают некоторую площадку S, то поток вектора напряженности (раньше мы называли число силовых линий через площадку) будет определяться формулой:
где En – произведение вектора  на нормаль
на нормаль  к данной площадке (рис. 2.5).
к данной площадке (рис. 2.5).
Рис. 2.5
Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности ФЕ через эту поверхность.
В векторной форме можно записать 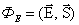 – скалярное произведение двух векторов, где вектор
– скалярное произведение двух векторов, где вектор  .
.
Таким образом, поток вектора  есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным.
есть скаляр, который в зависимости от величины угла α может быть как положительным, так и отрицательным.
Рассмотрим примеры, изображенные на рисунках 2.6 и 2.7.
Для рисунка 2.6 – поверхность А1 окружает положительный заряд и поток здесь направлен наружу, т.е 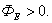 . Поверхность А2 – окружает отрицательный заряд, здесь
. Поверхность А2 – окружает отрицательный заряд, здесь 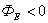 и направлен внутрь. Общий поток через поверхность А равен нулю.
и направлен внутрь. Общий поток через поверхность А равен нулю.
Для рисунка 2.7 – поток будет не равен нулю, если суммарный заряд внутри поверхности не равен нулю. Для этой конфигурации поток через поверхность Аотрицательный (подсчитайте число силовых линий).
27. Теорема Остроградского-Гаусса в интегральной и дифференциальной форме, ее физическое содержание
Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен алгебраической сумме зарядов, охваченных этой поверхностью.
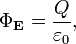
 Теорема Остроградского – Гаусса в интегральной форме
Теорема Остроградского – Гаусса в интегральной форме
 Теорема Остроградского – Гаусса в дифференциальной форме
Теорема Остроградского – Гаусса в дифференциальной форме
§
Электроемкостьюсистемы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

В системе СИ единица электроемкости называется фарад (Ф):
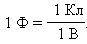
Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, – обкладками.
Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками . Но в других задачах пренебрежение полем рассеяния может привести к грубым ошибкам, так как при этом нарушается потенциальный характер электрического поля
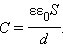
Электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:
Цилиндрический конденсатор – система из двух соосных проводящих цилиндров радиусов R1 и R2 и длины L. Емкости этих конденсаторов, заполненных диэлектриком с диэлектрической проницаемостью ε, выражаются формулами:
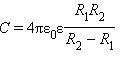
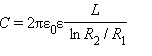 (Сферический и цилиндрический)
(Сферический и цилиндрический)
Конденсаторы могут соединяться между собой, образуя батареи конденсаторов. При параллельном соединении конденсаторов напряжения на конденсаторах одинаковы: U1 = U2 = U, а заряды равны q1 = С1U и q2 = C2U. Такую систему можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q1 q2 при напряжении между обкладками равном U. Отсюда следует 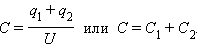
Таким образом, при параллельном соединении электроемкости складываются.
При последовательном соединении конденсаторов складываются обратные величины емкостей.
Формулы для параллельного и последовательного соединения остаются справедливыми при любом числе конденсаторов, соединенных в батарею.
33.Электрическое поле в диэлектриках. Модели диэлектриков. Поляризация диэлектриков, вектор поляризации. Напряженность поля в диэлектриках.
Типы диэлектриков
Диэлектриками называются вещества, которые при обычных условиях практически не проводят электрический ток. Удельное электрическое сопротивление диэлектриков ρ ~ 106 – 1015 Ом·м, тогда как у металлов ρ ~ 10-8 – 10-6 Ом·м.
Согласно представлениям классической физики, в диэлектриках в отличие от проводников, нет свободных носителей заряда – заряженных частиц, которые могли бы под действием электрического поля прийти в упорядоченное движение и образовать электрический ток проводимости.
К диэлектрикам относятся все газы, если они не подвергались ионизации, некоторые жидкости (дистиллированная вода, бензол и др.) и твердые тела (фарфор, слюда и др.). Твердые диэлектрики подразделяют на кристаллические, аморфные и тела сложного строения, состоящие из смеси монокристаллов, соединенных аморфной прослойкой (керамика, полимеры).
Все молекулы диэлектрика электрически нейтральны: суммарный заряд всех ядер молекулы равен суммарному заряду электронов
Вектор, направленный по оси диполя от отрицательного заряда к положительному, и равный расстоянию между ними, называется плечом диполя l. Вектор, совпадающий по направлению с плечом диполя и равный произведению заряда  на плечо l, называется электрическим моментом диполя или дипольным моментом.
на плечо l, называется электрическим моментом диполя или дипольным моментом.

Диэлектрики подразделяются на три основные группы.
К полярным диэлектрикам (H2O, NH3, СО и др.) относятся вещества, молекулы которых имеют асимметричное строение, т.е. центры «тяжести» положительных и отрицательных зарядов не совпадают (положительный заряд ядер, и отрицательный заряд электронов находятся в различных точках пространства). Эти молекулы обладают постоянным дипольным моментом.
К неполярным диэлектрикам относят вещества (N2, CO2, H2 и др.), молекулы которых имеют симметричное строение, т.е. центры «тяжести» положительных и отрицательных зарядов совпадают, и их дипольный момент равен нулю.
Третью группу диэлектриков составляют вещества (NaCl, KCl, KBr и др.), молекулы которых имеют ионное строение. Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. В этих кристаллах нельзя выделить отдельную молекулу, можно рассматривать как систему двух вдвинутых одна в другую ионных подрешеток. В таких диэлектриках дипольные моменты отсутствуют.
Во внешнем электрическом поле диэлектрик поляризуется. Диэлектрик поляризован, если он имеет результирующий дипольный момент отличный от нуля, а дипольные моменты молекул ориентированы по полю. Механизм поляризации различен для различных диэлектриков.
Электроннаяполяризация возникает в диэлектриках, состоящих из неполярных молекул. Если поместить диэлектрик во внешнее электрическое поле, то положительные заряды будут смещаться по направлению вектора напряженности электрического поля  , а отрицательные – в противоположном направлении. В результате неполярные молекулы приобретут наведенный (индуцированный) дипольный момент, направленный вдоль внешнего поля, т.е. диэлектрик поляризуется (рис. 2.2). Дипольный момент молекул пропорционален напряженности внешнего поля
, а отрицательные – в противоположном направлении. В результате неполярные молекулы приобретут наведенный (индуцированный) дипольный момент, направленный вдоль внешнего поля, т.е. диэлектрик поляризуется (рис. 2.2). Дипольный момент молекул пропорционален напряженности внешнего поля 
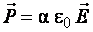 , (2.1)
, (2.1)
Где α – поляризуемость молекулы, зависящая только от объема молекулы.
 Электронная поляризация:
Электронная поляризация:
а) – внешнее поле отсутствует, б) – молекула диэлектрика
во внешнем электрическом поле
Ионная поляризация возникает в диэлектриках с ионными кристаллическими решетками. При помещении диэлектрика во внешнее электрическое поле подрешетки положительных ионов смещаются по направлению напряженности электрического поля Е, а отрицательные – против поля. В результате возникают индуцированные дипольные моменты, ориентированные по полю.
В целом процессы электронной и ионной поляризации сходны между собой. Оба эти явления можно рассматривать как разновидность деформационной поляризации, представляющий собой сдвиг зарядов друг относительно друга. На деформационную поляризацию не оказывает влияния температура. Данный вид поляризации не вызывает возникновения диэлектрических потерь и отличается большой скоростью установления состояния поляризации.
Ориентационная (дипольная) поляризация возникает в полярных диэлектриках (рис. 2.3). На каждый из зарядов диполя, внесенного в однородное электрическое поле с напряженностью 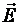 , будут действовать равные по модулю силы
, будут действовать равные по модулю силы 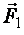 и
и 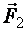 , направленные в противоположные стороны. Они создадут момент сил М, стремящийся повернуть молекулу-диполь так, чтобы его дипольный момент совпадал по направлению с вектором напряженности электрического поля. Вектор момента сил равен
, направленные в противоположные стороны. Они создадут момент сил М, стремящийся повернуть молекулу-диполь так, чтобы его дипольный момент совпадал по направлению с вектором напряженности электрического поля. Вектор момента сил равен 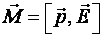 или по модулю
или по модулю 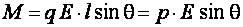 . Таким образом, каждая молекула-диполь будет испытывать ориентирующее действие поля (рис. 2.3).
. Таким образом, каждая молекула-диполь будет испытывать ориентирующее действие поля (рис. 2.3).
Рис. 2.3. Ориентационная поляризация
Ориентационная поляризация связана с тепловым движением молекул и зависит от температуры. При повышении температуры уменьшается степень упорядоченности их ориентации.
Степень поляризации диэлектрика характеризуется векторной величиной, называемой поляризованностью, которая определяется как дипольный момент единицы объема диэлектрика.
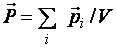
где 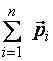 – суммарный дипольный момент всех молекул диэлектрика в объеме V,
– суммарный дипольный момент всех молекул диэлектрика в объеме V, 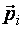 – дипольный момент одной молекулы.
– дипольный момент одной молекулы.
Поляризованность изотропного диэлектрика любого типа связана с напряженностью поля соотношением
 , (2.3)
, (2.3)
где  – диэлектрическая восприимчивость вещества,
– диэлектрическая восприимчивость вещества,  – электрическая постоянная.
– электрическая постоянная.
Диэлектрическая восприимчивость вещества характеризует способность диэлектрика к поляризации.
§
Законы Кирхгофа для разветвленной цепи (разветвленная цепь – электрическая цепь, содержащая узлы – места, где сходятся не менее трех проводников):
а) По первому закону Кирхгофа – алгебраическая сумма токов, сходящихся в узле, равна нулю  . Токи, приходящие к узлу, считаются положительными, а токи, отходящие от узла, отрицательными.
. Токи, приходящие к узлу, считаются положительными, а токи, отходящие от узла, отрицательными.
б)Второй закон Кирхгофа: в замкнутом контуре алгебраическая сумма произведений токов в участках на сопротивление этих участков равна алгебраической сумме электродвижущих сил, включенных в данный контур
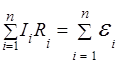 ,
,
где 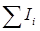 – алгебраическая сумма сил токов, сходящихся в узле;
– алгебраическая сумма сил токов, сходящихся в узле; 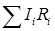 – алгебраическая сумма произведений сил токов на сопротивления замкнутых участков;
– алгебраическая сумма произведений сил токов на сопротивления замкнутых участков; 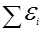 – алгебраическая сумма ЭДС источников тока на замкнутом участке цепи.
– алгебраическая сумма ЭДС источников тока на замкнутом участке цепи.
При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо:
1. Выбрать произвольное направление токов на всех участках цепи.
2. Выбрать направление обхода контура; произведение 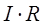 положительно, если ток на участке совпадает с направлением обхода, и, наоборот; ЭДС, действующие по выбранному направлению обхода (перемещение происходит внутри источника тока от катода к аноду), считаются положительными.
положительно, если ток на участке совпадает с направлением обхода, и, наоборот; ЭДС, действующие по выбранному направлению обхода (перемещение происходит внутри источника тока от катода к аноду), считаются положительными.
3. Составить столько уравнений, чтобы их число было равно числу неизвестных электрических величин; каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержавшийся в предыдущих контурах.
Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

Например, для рис. 148 первое правило Кирхгофа запишется так:
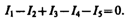
Первое правило Кирхгофа вытекает из закона сохранения электрического заряда. Действительно, в случае установившегося постоянного тока ни в одной точке проводника и ни на одном его участке не должны накапливаться электрические заряды. В противном случае токи не могли бы оставаться постоянными.
Второе правило Кирхгофа получается из обобщенного закона Ома для разветвленных цепей. Рассмотрим контур, состоящий из трех участков (рис. 149). Направление обхода по часовой стрелке примем за положительное, отметив, что выбор этого направления совершенно произволен. Все токи, совпадающие по направлению с направлением обхода контура, считаются положительными, не совпадающие с направлением обхода — отрицательными. Источники тока считаются положительными, если они создают ток, направленный в сторону обхода контура. Применяя к участкам закон Ома (100.3), можно записать:


Складывая почленно эти уравнения, получим
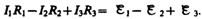 (101.1)
(101.1)
Уравнение (101.1) выражает второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов Ii на сопротивления Ri соответствующих участков этого контура равна алгебраической сумме э.д.с. , встречающихся в этом контуре:
(101.2)
При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо:
1. Выбрать произвольное направление токов на всех участках цепи; действительное направление токов определяется при решении задачи: если искомый ток получится положительным, то его направление было выбрано правильно, отрицательным — его истинное направление противоположно выбранному.
2. Выбрать направление обхода контура и строго его придерживаться; произведение IR положительно, если ток на данном участке совпадает с направлением обхода, и, наоборот, э.д.с., действующие по выбранному направлению обхода, считаются положительными, против — отрицательными.
3. Составить столько уравнений, чтобы их число было равно числу искомых величин (в систему уравнений должны входить все сопротивления и э.д.с. рассматриваемой цепи); каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах, иначе получатся уравнения, являющиеся простой комбинацией уже составленных.
В качестве примера использования правил Кирхгофа рассмотрим схему (рис. 150) измерительногомоста Уитстона.* Сопротивления R1, R2, R3и R4 образуют его «плечи». Между точками А и В моста включена батарея с э.д.с. и сопротивлением r, между точками С и D включен гальванометр с сопротивлением RG.Для узлов А, В и С, применяя первое правило Кирхгофа, получим
(10 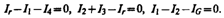 1.3)
1.3)
Для контуров АСВA, ACDA и CBDC, согласно второму правилу Кирхгофа, можно записать:
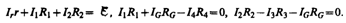 (101.4)
(101.4)
* Ч. Уитстон (1802—1875) — английский физик.
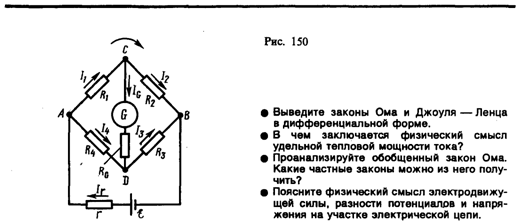
Если известны все сопротивления и э.д.с., то, решая полученные шесть уравнений, можно найти неизвестные токи. Изменяя известные сопротивления R2, R3 иR4, можно добиться того, чтобы ток через гальванометр был равен нулю (IG = 0). Тогда из (101.3) найдем
 (101.5)
(101.5)
а из (101.4) получим
 (101.6)
(101.6)
Из (101.5) и (101.6) вытекает, что
 (101.7)
(101.7)
Таким образом, в случае равновесного моста (IG = 0) при определении искомого сопротивления R1 э.д.с. батареи, сопротивления батареи и гальванометра роли не играют.
На практике обычно используетсяреохордный мост Уитстона (рис. 151), где сопротивления R3и R4 представляют собой длинную однородную проволоку (реохорд) с большим удельным сопротивлением, так что отношение R3/R4 можно заменить отношением l3/l4. Тогда, используя выражение (101.7), можно записать
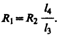 (101. 8)
(101. 8)
Длины l3 и l4 легко измеряются по шкале, a R2 всегда известно. Поэтому уравнение (101.8) позволяет определить неизвестное сопротивление R1.
РАЗВЕТВЛЕННЫЕ ЦЕПИ
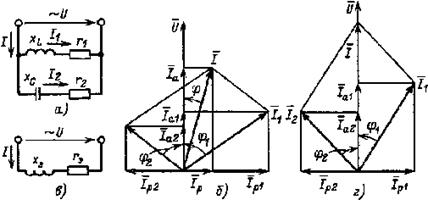
Параллельное соединение приемников. Вначале рассмотрим графоаналитический метод расчета цепи с параллельным соединением потребителей (рис. 2.16, а). Для такой цепи характерно то, что напряжения на каждой ветви одинаковы, общий ток равен сумме токов ветвей.
Ток в каждой ветви определяется по закону Ома:
| I1 = | U | ; I2 = | U | ; I3 = | U | (xL3 > xC3). |
| √r12 xL12 | √r22 xC22 | √r32 (xL3 — xC3)2 |
Угол сдвига φ между током каждой ветви и напряжением определяют с помощью cos φ:
| cos φ1 = | r1 | ; cos φ2 = | r2 | ; cos φ3 = | r3 | . | ||||||||||||||
| √r12 xL12 | √r22 xC22 | √r32 (xL3 — xC3)2 | ||||||||||||||||||
Общий ток в цепи, как следует из первого закона Кирхгофа, равен геометрической сумме токов всех ветвей:
Ī = Ī1 Ī2 Ī3.
Значение общего тока определяют графически по векторной диаграмме рис. 2.16, б.
Активная мощность цепи равна арифметической сумме активных мощностей всех ветвей:
Р = Р1 P2 P3.
Реактивная мощность цепи равна алгебраической сумме реактивных мощностей всех ветвей:
причем реактивную мощность ветви с индуктивностью берут со знаком плюс, ветви с емкостью — со знаком минус. Для цепи рис. 2.16 реактивная мощность равна
Q = QL1 — QC2 QL3 — QC3.
Полная мощность цепи
S = √P2 Q2.
Угол сдвига φ между общим током и напряжением определяют из векторной диаграммы или из выражения:
cos φ = P/S.
Графоаналитический метод не удобен для расчета разветвленных цепей: он отличается громоздкостью и невысокой степенью точности.
Для анализа и расчета разветвленных цепей переменного тока используют проводимости, с помощью которых разветвленную цепь можно преобразовать в простейшую цепь и аналитически рассчитать токи и напряжения всех ее участков.
В цепях постоянного тока проводимостью называется величина, обратная сопротивлению участка цепи:
g = 1/r
и ток в цепи выражается как произведение напряжения на проводимость:
I = Ug.
| Рис. 2.17. Электрическая цепь (а), ее векторная диаграмма (б) и эквивалентная схема (в); векторная диаграмма цепи при резонансе |
В цепях переменного тока существуют три проводимости — полная,
активная и реактивная, причем только полная проводимость является величиной, обратной полному сопротивлению последовательного участка цепи.
Выражения проводимостей в цепях переменного тока можно получить следующим образом.
Ток в каждом неразветвленном участке цепи раскладывают на две составляющие, одна из которых есть проекция на вектор напряжения (активная составляющая тока Ia ), а другая — на линию, перпендикулярную вектору напряжения (реактивная составляющая тока Iр ).
Активная составляющая тока определяет активную мощность
P = UI cos φ = UIa ;
реактивная составляющая тока — реактивную мощность
Q = UI sin φ = UIр.
Из векторной диаграммы цепи рис. 2.17, а, изображенной на рис. 2.17, б, следует, что активная составляющая тока I1 равна
| I1a = I1 cos φ1 = | U | r | = Ur1/z12 = Ug1. |
| z1 | z1 |
Величина
g1 = r1/z12
называется активной проводимостью ветви. Реактивная составляющая тока I1 равна
| Ilp = I1 sin φ1 = | U | xL | = UxL/z12 = Ub1. |
| z1 | z1 |
Величина
b1 = xL/z12 = bL1
называется реактивной проводимостью ветви цепи с индуктивностью и в общем случае обозначается bL.
Аналогично определяют активную g2 и реактивную b2 проводимости второй ветви цепи:
I2а = I2cos φ2 = U/z2 • r2/z2 = Ug2 ; g2 =r2 /z22 ;
I2p = I2 sin φ2 = U/z2• xC /z2 = Ub2; b2 = bC2 = xC2 /z22.
Реактивная проводимость ветви с емкостью в общем случае обозначается bC.
Вектор тока первой ветви равен геометрической сумме векторов активной и реактивной составляющих тока
Ī1 = Ī1а Ī1р,
а значение тока
I1 = √I1а2 I1р2.
Выразив составляющие тока через напряжение и проводимости, получим
I1 = √(Ug1)2 (UbL1)2 = U √g12 bL12 = Uу1 = U/z1,
где у1 = 1/z1 = √g12 bL12 — полная проводимость ветви.
Аналогично определяют и полную проводимость второй ветви:
у2 = 1/z2 = √g22 bС2.
Эквивалентные активную, реактивную и полную проводимости цепи получают следующим образом.
Вектор общего тока цепи равен геометрической сумме векторов токов Ī1 и Ī2:
Ī = Ī1 Ī2
и может быть выражен через активную и реактивную составляющие тока и эквивалентные проводимости всей цепи:
Ī = Īа Īр = Ūgэ Ūbэ = Uуэ = U/zэ .
Активная составляющая общего тока (см. рис. 2.17, б) равна арифметической сумме активных составляющих токов ветвей:
(2.24)
Iа = I1а I2а = Ug1 Ug2 = U(g1 g2) = Ugэ.
а реактивная составляющая — арифметической разности реактивных составляющих этих токов:
(2.25)
Iр = I1р I2р = UbL1 — UbC2 = U (bL1— bC2)= Ubэ .

| Рис. 2.18. К расчету разветвлен- ной цепи с использова- нием проводимостей |
Из выражений (2.24) и (2.25) следует, что эквивалентная активная проводимость цепи равна арифметической сумме активных проводимостей параллельно включенных ветвей:
(2.26)
gэ = g1 g2 … gn ,
а эквивалентная реактивная проводимость — алгебраической сумме реактивных проводимостей параллельно включенных ветвей:
(2.27)
bэ = bL1 bС2 … bLn bСп .
При этом проводимости ветвей с индуктивным характером нагрузки берут со знаком плюс, ветвей с емкостным характером нагрузки — со знаком минус. Полная эквивалентам проводимость цепи
(2.28)
уэ = 1/zэ = √gэ2 bэ2.
По эквивалентным активной, реактивной и полной проводимостям можно определить параметры эквивалентной схемы (рис. 2.17, в) цепи.
Эквивалентные активное, реактивное и полное сопротивления цепи определяют с помощью выражений
zэ = 1/уэ , rэ = gэzэ2, хэ = bэzэ2.
Необходимо отметить, что если ΣbL > ΣbC, то эквивалентное сопротивление хэ будет индуктивным, если ΣbC> ΣbL —емкостным.
Смешанное соединение потребителей.Расчет цепи при смешанном соединении потребителей (рис. 2.18, а) может быть произведен путем замены ее простейшей эквивалентной цепью. Для этого вначале определяют активные, реактивные и полные проводимости параллельно включенных ветвей: g1, g2, b1, b2, у1, у2.
Затем находят эквивалентные активную, реактивную и полную проводимости параллельного участка цепи:
gэ = g1 g2;
bэ = b1 b2;
уэ = √gэ2 bэ2.
Далее определяют эквивалентные активное, реактивное и полное сопротивления параллельного участка цепи:
rэ = gэzэ2; xэ = bэzэ2; zэ = 1/уэ.
В результате расчетов цепь может быть заменена эквивалентной цепью (рис. 2.18, б), где все сопротивления включены последовательно. Общие активное, реактивное и полное сопротивления цепи равны
rоб = rэ r.
xоб = x ± xэ,
zоб = √rоб2 xоб2.
Цепь приобретает простейший вид, изображенный на рис. 2.18, в. Общий ток цепи определяют по закону Ома:
I = U/zоб
Напряжение между точками а и b
Uab = Izэ = I/уэ .
Токи в параллельных ветвях равны
I1 = Uab у1, I2 = Uab у2.

