Закон эквивалентов. понятие эквивалент. молярная масса эквивалента
Одним из основных законов химии является закон эквивалентов, открытый в конце 18 века: массы элементов; соединяющихся друг с другом, пропорциональны их эквивалентам:
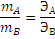
где mA, mВ – массы взаимодействующих веществ А и В;
ЭА и ЭВ – эквиваленты этих веществ.
Эквивалент – это реальная или условная частица, которая в кислотно-основных реакциях ионного обмена равноценна одному атому или одному иону водорода, а в окислительно-восстановительных реакциях одному электрону.
Массу одного моля эквивалента элемента называют молярной массой эквивалента MЭ(X). Значение эквивалента веществ зависит от того, в какой конкретной реакции участвует это вещество.
Молярная масса эквивалента химического элемента (MЭ(X)), а также простых или сложных веществ рассчитывается по формуле
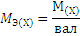
где M(X) – молярная масса; вал – суммарная валентность.
Для простых веществ суммарная валентность определяется произведением валентности атома химического элемента и числа атомов. Так, молярная масса эквивалента алюминия составляет MЭ(AI)=27/3=9 г∙моль-1. Молярные массы эквивалента кислорода и водорода следует запомнить, они равны соответственно MЭ(О)=16/2=8г∙моль-1, МЭ(Н)=1/1=1 г моль-1.
Молярные массы эквивалента сложных веществ вычисляются по их химическим формулам с учетом происходящих химических реакций.
К сложным веществам относятся оксиды, гидроксиды, соли.
Суммарная валентность оксидов равна произведению валентности кислорода (2) на количество атомов кислорода в молекуле. Суммарная валентность гидроксидов определяется их кислотностью, которая равняется числу замещенных гидроксильных групп. Суммарная валентность кислот равняется основности данных соединений, которая определятся числом замещенных атомов водорода. Суммарная валентность соли равняется произведению валентности катиона и количества катионов в молекуле, или валентности аниона и количества анионов в молекуле.
Молярная масса эквивалентов сложных веществ может быть определена как сумма молярных масс эквивалентов элементов или условных частиц, образующих данное вещество.
Мэ(оксиды)=Мэ(О) Мэ(элемента)=8 Мэ(элемента), т.к. Мэ кислорода величина постоянная, равна 8 г∙моль-1
Мэ(кислота)=Мэ(Н) Мэ(кислотного остатка)=1 Мэ(кислотного остатка), т.к. Мэ водорода величина постоянная, 1 г∙моль-1
Мэ(гидроксиды)=Мэ(OH—) Мэ(металла)=17 Мэ(металла), т.к. Мэ “OH” групп величина постоянная, равна 17 г∙моль-1.
Мэ(соли)=Мэ(катиона) Мэ(кислотного остатка).
Пример 1. Выразите в молях: а) 6,02∙1021молекул CO2; б) 1,20∙1024 атомов кислорода; в) 2,00∙1023 молекул воды. Чему равна мольная (молярная) масса указанных веществ?
Решение. Моль – это количество вещества, в котором содержится число частиц любого определенного сорта, равное постоянной Авогадро (6,02 ∙1023). Отсюда:
а) 6,02∙1021, т.е.0,01 моль; б) 1,20∙1024,т.е. 2 моль; в) 2,00∙1023м,т.е.1/3 моль.
Так как молекулярные массы СО2 и H2O и атомная масса кислорода соответственно равны 44; 18 и 16 а.е.м., то их мольные (молярные) массы равны: а) 44 г/моль; б) 18 г/моль; в) 16 г/моль.
Пример 2. Определите эквивалент (Э) и эквивалентную массу МЭ (Х) азота, серы и хлора в соединениях NHз ,H2S и HCl.
Решение. Масса вещества и количество вещества – понятия неидентичные. Масса выражается в килограммах (граммах), а количество вещества – в молях.
В данных соединениях с 1 моль атомов водорода соединяется 1/3 моль азота,1/2 моль серы и 1 моль хлора. Отсюда Э(N) =1/3 моль, Э(S) =1/2 моль, Э(Cl) =1 моль. Исходя из мольных масс этих элементов определяем их эквивалентные массы:
МЭ (N) =1/3∙14= 4,67 г/моль;
МЭ (S) =1/2∙32= 16 г/моль;
МЭ (Cl) =1∙35,45= 35,45 г/моль.
Пример 3.На восстановление 7,09 г оксида двухвалентного металла требуется 2,24 л водорода(н.у.). Вычислите эквивалентную массу оксида и эквивалентную массу металла. Чему равна атомная масса металла? Нормальные условия по Международной системе единиц (СИ): давление 1,013∙105Па (760 мм рт. ст.=1 атм), температура 273 К или 00 С.
Решение. Согласно закону эквивалентов массы (объемы) реагирующих друг с другом веществ m1 и m2 пропорциональны их эквивалентным массам (объемам):
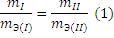
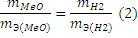
Если одно из веществ находится в газообразном состоянии, то, как правило, его количество измеряется в объемных единицах (см3, л, м3).
Объем, занимаемый при данных условиях мольной или эквивалентной массой газообразного вещества, называется мольным или, соответственно, эквивалентным объёмом этого вещества. Мольный объём любого газа при н.у. равен 22,4 л. Отсюда эквивалентный объём водорода VmЭ (Н2) = 22,4/2=11,2 л, а эквивалентный объём кислорода равен 5,6 л.
В формуле (2) отношение mН2/mЭ(Н2) заменяем равным ему отношением VН2/VmЭ(Н2), где VН2— объём водорода, VmЭ(MeO) — эквивалентный объём водорода:
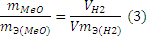
Из уравнения (3) находим эквивалентную массу оксида металла mЭ (МеО):
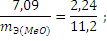
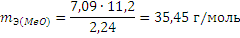
Согласно закону эквивалентов mЭ (МеО) = mЭ (Ме) mЭ (О2), отсюда
mЭ (Ме) = mЭ (МеО) — mЭ (О2) =35,45- 8 = 27,45 г/моль.
Мольная масса металла определяется из соотношения mЭ = А/В , где
mЭ — эквивалентная масса, А- мольная масса металла, В- стехиометрическая валентность элемента; А= mЭ ∙ В =27,45∙2 = 54,9 г/моль. Так как атомная масса в а.е.м. численно равна мольной (молярной) массе, выражаемой в г/моль, то искомая атомная масса металла 54,9 а.е.м.
Пример 4. Вычислите эквиваленты и эквивалентные массы H2SО4 и Аl(OH)3 в реакциях, выраженных уравнениями:
H2SО4 КОН= КHSО4 H2O (1)
H2SО4 Мg= MgSО4 H2 (2)
Al(ОH)3 НCl= Al(ОH)2 Cl H2O (3)
Al(ОH)3 3НNO3 = Al(NО3)3 3H2O (4)
Решение. Эквивалент (эквивалентная масса) сложного вещества, как и эквивалент (эквивалентная масса) элемента, может иметь различные значения и зависит от того, в какую реакцию обмена вступает это вещество. Эквивалентная масса кислоты (основность) равна мольной массе (М), деленной на число атомов водорода, замещенных в данной реакции на металл (на число вступающих в реакцию гидроксильных групп). Следовательно, эквивалентная масса H2SО4 в реакции (1) МH2SО4=98 г/моль, а в реакции (2) МH2SО4/2=49 г/моль. Эквивалентная масса Al(OH) 3 в реакции (3) МAl(ОH)3 = 78 г/моль а в реакции (4) МAl(ОH)3/3 =26 г/моль.
Пример 5. Сколько металла, эквивалентная масса которого 12,16 г/моль, взаимодействует с 310 см3 кислорода (н.у.)?
Решение. Так как молярная масса О2 (32 г/моль) при н.у. занимает объем 22,4 м, то объем молярной массы эквивалента кислорода (8 г/моль) будет равен 22,4/4 = 5,6 = 5600 см3. По закон эквивалентов
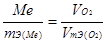 или
или 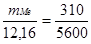 ,
,
откуда тМе= 12,16 ∙ 310/5600 = 0,673 г.
Пример 6.Из 3,85 г нитрата металла получено 1,60 г его гидроксида. Вычислите молярную массу эквивалента металла (тЭ(Ме) ).
Решение. При решении задачи следует иметь в виду: а) молярная масса эквивалента гидроксида равна сумме молярных масс эквивалентов металла и гидроксильной группы; б) молярная масса эквивалента соли равна сумме молярных масс эквивалентов металла и кислотного остатка. Вообще молярная масса эквивалента химического соединения равна сумме молярных масс эквивалентов составляющих его частей.
Учитывая сказанное, подставляем соответствующие данные в уравнение (1) примера 3:
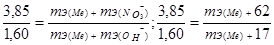
mЭ(Ме) = 15 г/моль
Пример7. В какой массе Са(ОН)2 содержится столько же эквивалентных масс, сколько в 312 г А1(ОН)3?
Решение. Молярная масса эквивалента А1(ОН)3 равна 1/3 его молярной массы, т.е. 78/3 = 26 г/моль. Следовательно в 312 г А1(ОН)3 содержится 312/26 =12 эквивалентов. Молярная масса эквивалента Са(ОН)2 равна ½ его молярной массы, т.е. 37 г/моль. Отсюда 12 эквивалентов составляют 37 г/моль ∙ 12 моль = 444 г.
Пример 8.Вычислите абсолютную массу молекулы серной кислоты в граммах.
Решение. Моль любого вещества содержит постоянную Авогадро NAструктурных единиц (в нашем примере молекул). Молярная масса H2SO4 равна 98,0 г/моль. Следовательно, масса одной молекулы 98/(6,02∙1023) = 1,63∙10-22г.
§
Три параметра – объем V, давление P и температура T (T=273 t) – определяет физическое состояние газа. Давление 1,013∙105Па (760 мм рт. ст.) и температура 273 К или 0оС называют нормальными условиями состояния газа, что в буквенных обозначениях этих величин указывается индексом: Po, To, to. Объем газа при н.у. – Vo.
Закон Бойля – Мариотта. При постоянной температуре объем данной массы газа изменяется обратно пропорционально давлению:
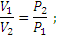
или V1 P1= V2 P2=V3P3…, т.е. V∙P=const.
Закон Гей-Люссака. При постоянном давлении объем данной массы газа меняется прямо пропорционально абсолютной температуре
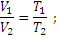
При постоянном объеме:
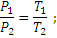
Уравнение Менделеева – Клапейрона. Объединение законов Бойля, Мариотта и Гей-Люссака дает уравнение состояния газа
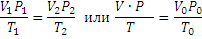
если одно из состояний является нормальным. Для любого газа количеством вещества 1 моль величина 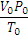 постоянна и одинакова, поэтому её называют универсальной газовой постоянной R. Если
постоянна и одинакова, поэтому её называют универсальной газовой постоянной R. Если 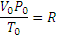 , то VP=RT, а для газа количеством вещества n моль Vp=nRT. Так как n равно отношению массы вещества к его молярной массе, то
, то VP=RT, а для газа количеством вещества n моль Vp=nRT. Так как n равно отношению массы вещества к его молярной массе, то 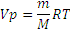 – это равенство и является урав-нением Менделеева – Клапейрона в окончательном виде. Числовые значения универсальной газовой постоянной зависят от того, в каких единицах выражены объем и давление газа. Так в системе СИ единица объема – кубический метр, а единица давления – паскаль (Па), т.е. сила в 1 ньютон, приходящаяся 1м2 площади (Н/м2). Ньютон (Н) – сила сообщающая массе в кг ускорение в 1 м/с. Джоуль – работа силы в 1 ньютон на расстоянии в 1м. Подставляя соответствующие значения в формулу
– это равенство и является урав-нением Менделеева – Клапейрона в окончательном виде. Числовые значения универсальной газовой постоянной зависят от того, в каких единицах выражены объем и давление газа. Так в системе СИ единица объема – кубический метр, а единица давления – паскаль (Па), т.е. сила в 1 ньютон, приходящаяся 1м2 площади (Н/м2). Ньютон (Н) – сила сообщающая массе в кг ускорение в 1 м/с. Джоуль – работа силы в 1 ньютон на расстоянии в 1м. Подставляя соответствующие значения в формулу 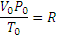 получим
получим
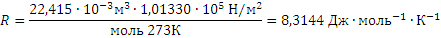
Если объем газа измерен в литрах, а давление газа в мегапаскалях (МПа=106Па), то R=0,083л∙МПа∙моль-1∙К-1. В расчетах обычно используют числа, имеющие три значащие цифры, что дает вполне достаточную точность: 22,4910-3 м3, 22,4 л, 273 К, 8,31 Дж∙моль-1∙К-1.
Согласно закону Авогадро, в равных объемах любых газов, взятых при одной и той же температуре и одинаковом давлении, содержится одинаковое число молекул.
Иными словами, одно и то же число молекул любого газа занимает при одинаковых условиях один и тот же объем. Вместе с тем 1 моль любого газа содержит одинаковое число молекул. Следовательно, при одинаковых условиях 1 моль любого газа занимает один и тот же объем. Этот объем называется мольным объемом газа и при нормальных условиях (00С, давление 101,325 кПа) равен 22,4 л.
Пример 1.Определить объём, занимаемый 5,25 г азота при 260С и давлении 98,9 кПа (742 мм рт.ст.).
Решение. Зная мольный объём и мольную массу (28,0 г/моль) азота, находим объём, который будут занимать 5,25 г азота при нормальных условиях:
28,0 г азота занимают объём 22,4л
5,25 г азота занимают объём VO ,
откуда VO = 5,25∙22,4/ 28,0 = 4,20 л
Затем приводим полученный объём к указанным в задаче условиям:
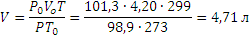
Пример 2.При250С и давлении 99,3 кПа (745 мм рт.ст.) некоторое количество газа занимает объём 152 мл. Найти, какой объём займет это же количество газа при 00С и давлении101,33 кПа.
Решение. Подставляя данные задачи в последнее уравнение, получаем:
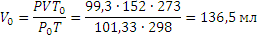
Пример 3.Некоторый газ массой 5,6 г занимает объём 4,84 л притемпературе 170С и давлении 0,997∙105 Па. Чему равна относительная молекулярная масса этого газа?
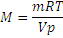 Решение. Из уравнения Менделеева-Клайперона ,откуда
Решение. Из уравнения Менделеева-Клайперона ,откуда
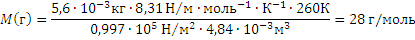
Так как числовое значение молярной массы, выраженной в г/моль, равно относительной молекулярной массе, т.е. {M}=Mr , то Mr = 28.
§
С увеличением значений n и ℓ энергия электрона возрастает. Состояния электрона с одинаковым значением энергии называют вырожденными, а число таких состояний- степенью или кратностью вырождения.
Волновая функция при определенных значениях трех квантовых чисел(n,ℓ и mℓ) φnℓmℓ описывает состояние электрона при его орбитальном движении, которое называют атомной орбиталью (АО). Волновую функцию, зависящую от всех четырех квантовых чисел, называют спин-орбиталью.
Каждой АО соответствует область пространства определенного размера, формы и ориентации, равноценная понятию электронного облака. С целью упрощении оба эти понятия отождествляются, и когда говорят о форме АО или об электроне, находящемся на АО, то имеется в виду не сама волновая функция, а только то, что она определяет – форма электронного облака и энергетическое состояние электрона.
Число АО в пределах энергетического подуровня определяется числовым значением магнитного квантового числа (2 ℓ 1). Число АО в пределах всего энергетического уровня равно сумме АО всех его подуровней:
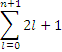
Вероятность обнаружения электрона даже на больших расстояниях от ядра только приближается к нулевому значению, поэтому электронное облако не имеет четких границ. В связи с этим введено понятие граничная поверхность, т.е. поверхность с равной электронной плотностью, ограничивающей объем, который включает 90% заряда и массы электрона. Форма и размер граничной поверхности считаются формой и размером электронного облака.
Графики радиального распределения вероятности нахождения электрона в атоме дают возможность определить форму электронных облаков. S-Электронное облако (ℓ=0) обладает сферической симметрией. р-электронное облако (ℓ=1) имеет осевую симметрию и форму, схожую с объёмной восьмеркой или гантелью. Относительное пространственное положение электронных облаков p-подуровня определяется осями координат, вдоль которых они вытянуты, поэтому для них приняты обозначения: рх , рy , рz, d-электронные облака (ℓ=2) имеют более сложную форму.
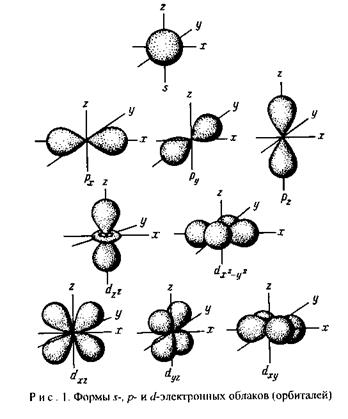
Последовательное распределение электронов в атоме по мере увеличения значений n и ℓ при данном n выражается электронными формулами или электронными конфигурациями. В первом случае энергетические уровни обозначают цифрами, а подуровни- буквами с верхним индексом, указывающим число электронов. Во втором случае атомные орбитали условно обозначают квантовыми ячейками □ , а электроны – векторами, что дает возможность показать различие в ориентации их спинов: ↑ и ↓ . Так, строение атома фтора выражается электронной формулой 1s2 2s2 2p5 электронной конфигурацией:
Так как химическая характеристика элемента определяется прежде всего строением внешнего, а затем предвнешнего электронного слоя, то часто ограничиваются электронными формулами или конфигурациями только этих электронных слоев.
Заполнение АО в многоэлектронных атомах основано на принципе наименьшей энергии, т.е. каждый электрон занимает ту из доступных для него орбиталей, на которой его энергия будет наименьшей.
При заполнении АО действует принцип Паули, который говорит о том, что в атоме не может быть двух электронов, имеющих одинаковый набор значений для всех четырех квантовых чисел. Состояние электронов в атоме должно отличаться значением хотя бы одного квантового числа. Так, если два электрона имеют одинаковые квантовые числа n, ℓи mℓ. т.е. находятся на одной и той же АО, образуя двухэлектронное облако, то они должны отличаться значением четвертого квантового числа mS., поэтому их спины будут антипараллельными ↑↓ .
Принцип Паули определяет емкость (максимальное число электронов) энергетических уровней и подуровней, которая соответственно равна 2n2 и 2(2ℓ 1), т.е. удвоенному числу АО.
Заполнение энергетических подуровней подчиняется правилу Гунда, согласно которому электроны располагаются на вырожденных АО так, чтобы их суммарный спин был бы наибольшим, т.е. заполнение идет сначала только по одному электрону. Примером может быть р-подуровень в атомах бора, углерода и азота:
В атомах элементов кислорода, фтора и неона эти АО последовательно заполняются до двух электронов.
Закономерная последовательность заполнения энергетических уровней и подуровней в атомах с увеличением порядкового номера элемента выражается правилом Клечковского, которое называют также правилом суммы n ℓ. Согласно этому правилу порядок заполнения определяется возрастанием этой суммы , а при одинаковом ее значении первым заполняется подуровень с меньшим значением n в этой сумме:
1s→2s→2p→3s→3p→4s→3d→(n ℓ):1 0=1 2 0=2 2 1=3 3 0=3 3 1=4 4 0=4 3 2=5
Правило Клечковского позволяет заранее предвидеть появление в периодической системе Д. И. Менделеева рядов из d-, а затем из f- элементов, которые вклиниваются между s- и p- элементами того же большого периода. Правило позволяет также предсказать структуру пока еще не существующих периодов.
Пример 1.Составьте электронные формулы атомов элементов с порядковыми номерами 16 и 22. Покажите распределение электронов этих атомов по квантовым (энергетическим) ячейкам.
Решение. Так как число электронов в атоме того или иного элемента равно его порядковому номеру в таблице Д. И. Менделеева, то на основании вышеизложенного для элементов №16 (сера) и №22 (титан) электронные формулы имеют вид
16S 1S2 2S2 2P6 3S2 3P4
22TI 1S2 2S2 2P6 3S2 3P6 4S2 3d2 , а распределение электронов по энергетическим ячейкам следующее:
| s | p | d | |||||||
| n=3 | ↑↓ | ↑ | ↑ | ||||||
| n=2 | ↑↓ | ↑↓ | ↑↓ | ↑↓ | |||||
| n=1 | ↑↓ |
| s | p | d | f | |||||||||||||
| n=4 | ↑↓ | |||||||||||||||
| n=3 | ↑↓ | ↑↓ | ↑↓ | ↑↓ | ↑ | ↑ | ||||||||||
| n=2 | ↑↓ | ↑↓ | ↑↓ | ↑↓ | ||||||||||||
| n=1 | ↑↓ |
§
Количественным выражением тенденции атома к изменению конфигурации внешнего электронного слоя за счет отдачи или присоединения электронов являются: энергия ионизации (ЕИ) или ионизационный потенциал (I) и сродство к электрону (СЭ). Первая величина оценивает способность свободного атома отдавать свои электроны, а вторая присоединять электроны.
Энергия ионизации, необходимая для отрыва электрона от свободного невозбужденного атома, обычно выражается в электронвольтах (эВ), а соответствующий ионизационный потенциал- в вольтах (В).Численно обе величины одинаковы. В обозначении потенциала индексом указывается, какой по счету электрон отрывается от исходного атома. Для первого потенциала индекс часто опускается. Число возможных ионизационных потенциалов для атома равно числу содержащихся в нем электронов, а их значения увеличиваются в ряду: I1< I2< I3<……
Резкое увеличение ионизационного потенциала с уменьшением для электрона главного квантового числа n подтверждает распределение электронов в атоме по энергетическим уровням или электронным слоям.
Сродство к электрону количественно оценивается энергетическим эффектом, сопровождающим присоединение электрона к свободному атому: А ē → Ā СЭ. Эта величина может иметь как положительное, так и отрицательное значение.
Наибольшее сродство к электрону имеют галогены и кислород. Отрицательное значение этой величины имеют благородные газы и некоторые другие элементы, например, для Не, Кr, Са оно соответственно равно -0,22; -0,42; -1,93 эВ. Отрицательной величиной является сродство атомов всех элементов ко второму электрону; для кислорода это -8,3 эВ. Таким образом, существование многозарядных отрицательных ионов энергетически невыгодно, поэтому даже в кристаллических оксидах наиболее активных металлов (Na2O, CaO) реальный заряд атома кислорода имеет значение не больше -1.
Электроотрицательность (ЭО) – понятие, определяющее свойства связанных атомов. Эта величина характеризует способность данного атома смещать на себя электронную плотность (электроны) атомов других элементов, с которыми он связан в химическом соединении. Электроотрицательность для элемента можно выразить полусуммой значений его ионизационного потенциала и сродства к электрону: (I CЭ)/2. Для практических целей удобнее пользоваться не абсолютным, а относительным значением ЭО. В этом случае электроотрицательность фтора принимается равной 4,0. Тогда ЭО(О)=3,5; ЭО(LI)= 0,98 и т.д. Фтор и кислород имеют самые высокие значения ЭО. Таблицы, в которых элементы располагаются в определенном порядке по значению их электроотрицательностей, позволяют определить направление смещения электронных плотностей между атомами в молекулах их соединений.
Степень окисления – понятие, определяющее число электронов, смещенных от менее электроотрицательного к более электроотрицательному атому при образовании между ними химической связи.
Степень окисления атомов в молекуле обозначают арабской цифрой (со знаком перед цифрой), расположенной над символом элемента. Например,
.Дляопределения степени окисления атомов в свободном состоянии и в химических соединениях следует руководствоваться следующими правилами.
1. Атомы кислорода в соединениях проявляют главным образом степень окисления, равную -2 (во фторкислороде OF2 и пероксидах М2О2 степень окисления кислорода равна соответственно 2 и -1). Для водорода характерная степень окисления 1, но встречается и -1 (в гидридах активных металлов, например NaH или CaH2 ).
2. Степень окисления атомов в простых ионных соединениях для данного иона равна по знаку и величине его электрическому заряду. Например, в хлориде калия степень окисления калия равна 1,а хлора-1, что обозначается соответствующей цифрой и знаком над символом элемента К 1Cl-1
3. Если молекула образована за счетковалентной связи, то степень окисления более электроотрицательного атома обозначают со знаком минус, а менее электроотрицательного – со знаком плюс. Так в SО2 степень окисления cеры 4, а кислорода – 2.
4. Принимая во внимание, что молекулы электронейтральны, т.е. что алгебраическая сумма степеней окисления атомов в молекулах равна нулю, легко определить степень окисления элементов в них. Например, определим степень окисления серы в Н2SO3 : степень окисления водорода равна 1, кислорода -2,тогда степень окисления серы Х определится из уравнения ( 1)2 Х (-2)3=0, откуда Х= 4.
5. Степень окисления атомов в молекулах, состоящих из одинаковых атомов, равна нулю, например, H20, P20, O20 и др. Степень окисления металлов в элементарном состоянии согласно рентгенографическим исследованиям, установившим равномерное распределение электронной плотности в них, также считается равной нулю ( Na0, Ca0, Al0 и др.)
Знание степени окисления элемента в тех или иных соединениях позволяет охарактеризовать химические свойства вещества. Так, из соединений кислорода, в которых он проявляет различные степени окисления
| -2 | -1 | 1 | 2 | |
| Н2О | Н2O2 | О2 | О2F2 | OF2 |
наиболее устойчивы вещества, в которых его степень окисления равна -2 или 0 (Н2О и О2), так как это отвечает минимуму энергии (т.е. наименьшему запасу энергии и, следовательно, наиболее устойчивому состоянию).
Соединения О2F2 ,и OF2 –сильные окислители, так как в них кислород находится в положительной степени окисления 1 и 2, а потому, обладая большим запасом (большим сродством к электрону), они будут сильно притягивать электроны вследствие стремления кислорода перейти в наиболее устойчивые для него состояния.
Кислород в пероксиде водорода находится, в промежуточной степени окисления, поэтому он будет или повышать степень окисления до 0 (проявляя восстановительные свойства), или понижать до -2 (являясь окислителем). Очевидно также, что свободный кислород проявляет окислительные свойства.
Следовательно, зная степень окисления атома данного элемента в соединении, можно определить, восстановителем или окислителем является это соединение. Например, элементы шестой главной подгруппы сера, селен и теллур в своей высшей степень окисления 6 в концентрированных кислотах Н2SO4, Н2SeO4 , H6TeО6 являются только окислителями, так как больше не могут отдавать электронов. Сера, селен и теллур в низшей степень окисления -2 в соединениях Н2S, Н2Se, H2 Te проявляют только восстановительные свойства, так как больше не могут присоединять электронов. Атомы этих элементов в промежуточной степени окисления 4 в соединениях типа Н2СO3, могут быть в зависимости от условий как, восстановителями, так и окислителями. Причем с более сильным окислителем они будут играть роль, восстановителя, а с более сильным, восстановителем -роль окислителя. Таким образом, атомы этих элементов в степени окисления 6 проявляют аналогичные свойства и значительно отличаются от атомов, находящихся в степени окисления 4 или тем более в степени окисления-2. Это относится и к другим главным и побочным подгруппам периодической системы Д.И Менделеева, элементы которых проявляют различные степени окисления.
§
Метод валентных связей (ВС) рассматривает химическую связь как результат притяжения ядер двух атомов к одной или нескольким общим для них электронным парам. Такая двухэлектронная и двуцентровая (двуядерная) связь, локализованная между двумя атомами, называется ковалентной.
Принципиально возможны два механизма образования ковалентной связи: 1) спаривание электронов двух атомов при условии противоположной ориентации их спинов; 2) донорно-акцепторное взаимодействие, при котором общей становится готовая электронная пара одного из атомов (донора) при наличии энергетически выгодной свободной орбитали другого атома (акцептора).
Причиной образования любого типа химической связи является понижение энергии системы, которое сопровождает этот процесс. Разность энергий начального и конечного состояния называется энергией связи (ЕСВ) и определяется количеством теплоты, выделяющейся при её образовании. Экспериментально удобнее находить эту величину по количеству энергии, которая затрачивается на разрыв данной связи. Энергия химических связей оценивается значениями порядка 125-1050 кДж/моль.
Расстояние между ядрами двух атомов, при котором силы притяжения уравновешиваются силами отталкивания и система имеет минимальную энергию, называется равновесным или длиной связи d. Длина и энергия связи зависят от её кратности, которая определяется числом электронных пар, связывающих два атома. С увеличением кратности уменьшается длина связи и увеличивается её энергия, например, эти величины для связей С-С1 С=С1 С=С соответственно равны (в нм и кДж) 0,154 и 548, 0,155 и 598, 0,120 и 838. Наоборот, увеличение радиусов атомов, образующих связь приводит к возрастанию ее длины и уменьшению энергии.
Во многих случаях число неспаренных электронов в атоме оказывается меньшим числа образованных им связей. Это объясняется тем, что при возбуждении атома происходит распаривание одной или нескольких электронных пар с последующим переходом одного электрона от каждой на свободную и энергетически доступную орбиталь более высокого подуровня. Такой процесс называют промотированием, а энергия, которая на это затрачивается, энергией промотирования Епром. Для атома серы кроме основного состояния (2↑) возможны два возбужденных S(4↑) и S(6↑) за счет перехода соответственно одного или двух электронов на 3d-орбитали.
Свойства ковалентной связи: насыщаемость, направленность и поляризуемость.
Насыщаемость ковалентной связи обусловлена ограниченными валентными возможностями атомов, т.е. их способностью к образованию строго определенного числа связей, которое обычно лежит от 1 до 6. Общее число валентных орбиталей в атоме, т.е. тех, которые могут быть использованы для образования химических связей, определяет максимально возможную ковалентность элемента. Число уже использованных для этого орбиталей, определяет ковалентность элемента в данном соединении.
Если атом образует все связи только за счет спаривания электронов, то обычно говорят просто о его валентности, которая определяется числом одноэлектронных орбиталей или числом неспаренных электронов его атома в основном или возбужденном состоянии.
Характер участия каждого вида АО в образовании связи (спаривание, донорная и акцепторные функции) графически изображают знаками:
Элементы 2-го периода периодической системы имеют только 4 валентных АО (одна 2S- и три 2P), поэтому их максимальная ковалентность равна 4. Число валентных электронов в атомах элементов, расположенных левее углерода, меньше числа АО, а в атомах элементов, расположенных правее, наоборот, больше. Поэтому первые могут быть акцепторами, а вторые – донорами электронных пар. В своем обычном валентном состоянии атом углерода имеет 4 неспаренных электрона, что совпадает с числом валентных АО, поэтому связей по донорно-акцепторному организму он не образует.
Направленность ковалентной связи является результатом стремления атомов к образованию наиболее прочной связи за счет возможно большей электронной плотности между ядрами. Это достигается при такой пространственной направленности перекрывания электронных облаков, которая совпадает с их собственной. Исключение составляют s-электронные облака, поскольку их сферическая форма делает все направления равноценными. Для p- и d- электронных облаков перекрывание осуществляется вдоль оси, по которой они вытянуты, а образующая при этом связь называется δ-связью. δ-связь имеет осевую симметрию и оба атома могут вращаться вдоль линии связи, т.е. той воображаемой линии, которая проходит через ядра химически связанных атомов. Это исключает возможность образования пространственных изомеров.
После образования между двумя атомами δ-связи для остальных электронных облаков той же формы и с тем же главным квантовым числом остается только возможность бокового перекрывания по обе стороны от линии связи, через которую в этом случае проходит одна узловая плоскость. В результате образуется π-связь. Таким образом, каждая кратная связь всегда содержит только одну δ-связь. Примером может быть молекула азота. Число δ-связей, которые образует центральный атом в сложных молекулах или ионах, определяет для него значение координационного числа. Например, в молекуле NН3 и ионе NН4 для атома азота оно равно трем.
Образование δ-связей фиксирует пространственное положение атомов относительно друг друга, поэтому число δ-связей и углы между линиями связи, которые называют валентными, определяют пространственную геометрическую конфигурацию молекул и комплексных ионов, что находит отражение в соответствующих геометрических моделях.
Связи, образованные атомом за счет орбиталей с различным значением ℓ, должны быть энергетически неравноценными, что, однако, не подтверждается экспериментом. Противоречие устраняется идеей гибридизации (Л. Полинг), согласно которой при образовании связей орбитали разной симметрии смешиваются и переходят в гибридные АО одинаковой формы и одинаковой усредненной энергии, что обеспечивает равноценность образуемых ими связей. Возможность гибридизации определяют три условия:
1. небольшая разница в энергии исходных АО, с увеличением этой разницы уменьшается устойчивость их гибридного состояния и прочность образуемых ими связей;
2. достаточная плотность электронных облаков, что определяется значением главного квантового числа;
3. достаточная степень перекрывания гибридных АО с орбиталями других атомов при образовании связей, что закрепляет гибридное состояние и делает его более устойчивым.
Число гибридных орбиталей равно числу исходных. Найти их можно методом линейной комбинации (сложение и вычитание) исходных АО (ЛКАО). Чем больше вклад АО в исходную волновую функцию, тем больше сходство с ней проявляет гибридная орбиталь. Несимметричная форма гибридных орбиталей обусловлена тем, что, с одной стороны, от ядра электронная плотность возрастает за счет сложения волновых функций с одинаковыми знаками, а с другой- уменьшается за счет сложения тех же функций с разными знаками, что равносильно их вычитанию. Такая форма гибридных орбиталей выгодна для образования более прочных связей.
Относительное пространственное положение гибридных орбиталей в атоме определяется корреляцией электронов по заряду и спину, согласно которой электроны с параллельными спинами стремятся находиться возможно дальше друг от друга, что уменьшает силы отталкивания и таким образом понижает энергию системы. В случае двух гибридных орбиталей наиболее энергетически выгодным будет их положение вдоль одной прямой с ориентацией в противоположных направлениях, что определяет линейную конфигурацию соответствующих молекул.
Sp2 –гибридизация дает три гибридных орбитали, которые направлены от центра к вершинам правильного треугольника и валентный угол в этом случае равен 1200 . Такая гибридизация валентных орбиталей осуществляется в молекулах ВF3 и ВСl3 .
Четыре Sp3 гибридные орбитали δ направлены к вершинам правильного тетраэдра под углом 1090. Примером тетраэдрических молекул могут быть СН4, СCl4 и ион NН4 .
В гибридизации могут участвовать не только одноэлектронные, но также и двухэлектронные АО. В этом случае на гибридных орбиталях остается такое число неподеленных, т.е. не принявших участия в образовании связей, электронных пар (НП), которое было на исходных АО. Не принимают участия в гибридизации свободные АО и те из одноэлектронных, которые образуют π-связи.
Геометрическая конфигурация молекул полностью определяется типом гибридизации орбиталей центрального атома только при условии, что все гибридные АО участвуют в образовании связей. Если же хотя бы на одной из них остается неподеленная электронная пара, то конфигурация, определяемая типом гибридизации, реализуется неполностью. Так, при наличии одного и того же типа гибридизации Sp3 в зависимости от числа неподеленных пар возможны четыре различных геометрических конфигураций молекул, как показано в таблице 2.
Таблица 2
Возможная геометрическая конфигурация молекул при Sp3 – гибридизации
| Число гибридных АО | Число НП | Координационное число связей | Геометрическая конфигурация | Примеры |
| Тетраэдр | СН4 ,СCl4 | |||
| Тригональная пирамида | N¨H3 | |||
| Угловая | H2 Ö: | |||
| Линейная | :B¨e: Сl ¨ |
Молекулы с кратными связями содержат π-связи, которые, не участвуя в гибридизации и не оказывая влияния на геометрическую конфигурацию молекул, стабилизируют гибридное состояние атомов. Число всех π-связей в молекуле равно кратности связи минус единица ( одна δ-связь). Число δ-связей определяется общей суммой простых и кратных связей. Так, в молекуле РОСI3 одна двойная и три простых связи, поэтому в ней содержится 3δ и одна π-связи.
Для определения типа гибридизации надо знать число гибридизующихся орбиталей центрального атома. Его можно найти вычитанием из общего числа валентных АО числа одноэлектронных, образующих π-связи. В схемах электронных конфигураций они отсчитываются справа налево, так как π-связи образуют, прежде всего, α- , а затем р-АО. Все оставшиеся валентные орбитали участвуют в гибридизации.
Присутствие в молекулах неподеленных электронных пар сказывается на величине валентных углов. Это связано с тем, что силы расталкивания больше, чем между относительно закрепленными связывающими электронными парами (СП). По убывающей силе расталкивания электронные пары могут быть расположены в следующем порядке:
НП – НП > НП-СП > СП-СП. В результате НП в известной степени как бы давят на электронные пары связи, что приводит к некоторому уменьшению валентного угла. Чем больше число НП, тем сильнее их действие. Так, в молекуле NН3 одна НП уменьшает тетраэдрический угол (~ 109 0 ) до 1070, а в молекуле Н2О 2НП уменьшают его до 104,50, Длина простых и двойных связей между центральным атомом и другими одинаковыми атомами оказывается по экспериментальным данным одинаковой. Это может быть объяснено делокализацией π-связей, т.е. их равномерным распределением между всеми связями, что в формулах указывается пунктирной линией.
В этих случаях кратность связи выражается дробным числом, в сульфат-ионе она равна 1,5. Это соответствует экспериментально найденной длине связи ( 0,149 нм), которая по своему значению является промежуточной между простой (0,160нм) и двойной (0,143 нм). Одновременно с делокализацией π-связей происходит также и делокализация зарядов, поэтому в оксокислотных ионах они сосредоточены не на атомах кислорода, а равномерно распределены по объёму всего иона .
Поляризуемость рассматривают на основе представлений о том, что ковалентная связь может быть неполярной ( чисто ковалентной) или полярной. В первом случае связь образуется между одинаковыми атомами, и симметричное распределение электронной плотности в межъядерном пространстве приводит к совпадению центров тяжести положительных и отрицательных зарядов. Полярная связь образуется в тех случаях, когда межъядерная электронная плотность смещается к атому с большей электроотрицательностью. Тогда центры тяжести ( ) и (-) зарядов не совпадают и возникает система ( электрический диполь) из двух равных по величине, но противоположных по знаку зарядов ( δ и δ-), расстояние между которыми называют длиной диполя ℓ. Степень полярности такой связи оценивается значением электрического момента диполя μ, равного произведению абсолютного заряда электрона ( q =1,60∙10-19 Кл) на длину диполя: μ = q∙ ℓ. Tак, если ℓ(Н-СI)=0.022нм или 22∙10-12м, то μ(Н-СI)=1,60∙10-19∙22∙10-12=3,52∙10-30 Кл∙м.
Экспериментально обычно определяют электрические моменты диполей и по ним находят длину диполя: ℓ= μ /q.
Моменты диполей –величины векторные, т.е. характеризуются направленностью (условно от положительного к отрицательному заряду).
Электрические моменты диполей молекул определяются геометрической (векторной) суммой моментов диполей связей. Например, μ линейной молекулы СО2 равен: μ (СО) μ (СО)=0 или для молекулы воды, в которой μ-связей Н-О направлены под углом 104,50, μ= 6,13∙10-30Кл∙м.
Поляризуемостью ковалентной связи называют её способность под действием внешнего электрического поля становиться полярной или более полярной. Постоянный момент диполя полярной связи μn в электрическом поле становиться больше на величину μi , равную временному моменту наведенного или индуцированного диполя : μ =μn μi.
Роль внешнего электрического поля могут играть заряженные частицы, входящие в состав самого соединения ( ионы или атомы с большим эффективным зарядом δ ).
Поляризующее действие иона приводит к деформации электронной оболочки его соседей, которое тем больше, чем больше их поляризуемость, т.е. способность к такой деформации. Чем больше заряд иона и меньше радиус, тем больше его поляризующее действие и меньше собственно поляризуемость.
Образование из атомов катионов и анионов сопровождается соответственно уменьшением и увеличением радиуса. Например, r (Na)= 0,189 и r (Na )= 0,098 нм; r (Cl)= 0,099 и r (Сl— )= 0,181 нм. Эти соотношения приводят к тому, что взаимодействие ионов сопровождается в основном только поляризацией аниона катионом. Для сложных анионов, благодаря их большим эффективным радиусам поляризующее действие и собственная поляризуемость сравнительно невелики и обычно не учитываются.
По возрастающей силе поляризующего действия все катионы можно объединить в три группы:
1. Катионы с завершенным устойчивым внешним электронным слоем типа благородного газа;
2. Катионы с незаконченным внешним электронным слоем- ионы α-элементов( Сr3 , Fe2 , Fe3 ,Mn2 и др.), ионы р-элементов ( TI , Pb2 , Bi3 и др.);
3. Катионы с 18-электронным слоем (Ag , Zn2 , TI3 и др.). Некоторые из ионов последней группы , например Нg2 легко деформируются, и тогда поляризованный анион индуцирует в них диполь, который , в свою очередь, усиливает деформацию электронной оболочки аниона, что называют дополнительным поляризационным эффектом [2].
Ионная связь
При полном смещении межъядерной электронной плотности к атому с большей электроотрицательностью длина диполя становится равной длине связи (ℓ=α), и атомы превращаются в положительно и отрицательно заряженные ионы, между которыми действуют силы электростатистического притяжения. Такую связь называют ионной. Степень полярности или ионности связи i определяется отношением ℓ/α, крайние значения которого 0 и1 соответствуют чисто ковалентной и чисто ионной связям. В остальных случаях эта величина имеет промежуточные значения, например, для молекулы НСl : α= 0,128 нм и ℓ = 0,0225 нм, откуда i = ℓ/α = 0,0225/0,1280 = 0,18 или точнее 0,20 (при учете влияния НР атома Сl). Таким образом, ионность связи Н-Сl составляет 20%, а эффективные заряды атомов δ 0,2 и -0,2 заряда электрона.
Чем больше разность электроотрицательностей ΔЭО для данной пары атомов, тем больше длина диполя и величина эффективных зарядов, а следовательно, тем больше и ионность связи:
| Cоединения | NaF | ZiF | NaCl | HF | HI |
| ΔЭО | 3,1 | 3,0 | 2,1 | 1,9 | 0,3 |
| Ионность , % | |||||
| Ковалентность,% |
Полного, т.е. 100%-ного, смещения электронной плотности на атом с большей ЭО не происходит даже в наиболее ионных соединениях, которыми являются бинарные соединения щелочных металлов с галогенами. Это объясняется как волновыми свойствами электронов, так и влиянием зарядов образовавшихся ионов на электронные оболочки друг друга, т.е. их взаимной поляризацией. Принято считать связь ионной, если ΔЭ0 > 1,9. Значения μ ионных молекул лежат в пределах 1,33∙10-30 Кл∙м.
Отрицательное сродство атомов ко второму электрону делает невозможным существование простых многозарядных ионов (О2- , N3- и т.д). Однако реально существует многозарядные сложные ионы (SO42- , PO43- и др.). Это объясняется делокализацией их зарядов, в результате которой эффективный заряд каждого атома, входящего в состав иона, не превышает заряда электрона, равного -1.
Ионная связь, в отличие от ковалентной характеризуется :
1. ненаправленностью, так как сферическое поле вокруг ионов во всех направлениях равноценно;
2. ненасыщаемостью, поскольку при взаимодействии ионов не происходит полной компенсации их силовых полей;
3. Координационными числами в ионных соединениях, которые определяются не электронной структурой атомов, а соотношением радиусов взаимодействующих ионов. Так, отношение
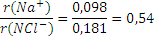
Это значение лежит в пределах 0,41 – 0,73, что определяет октаэдрическую координацию ионов, которая характеризует кристаллическую решетку хлорида натрия.
§
Существенные сведения относительно природы химической связи в металлах модно получить на основании двух характерных особенностей по сравнению с ковалентными и ионными соединениями. Металлы, во-первых отличаются от других веществ высокой электропроводностью и теплопроводностью, во-вторых, в обычных условиях являются кристаллическими веществами (за исключением ртути), структуры которых характеризуются высокими координационными числами.
Из первого характерного свойства металлов следует, что по крайней мере часть электронов может передвигаться по всему объема куска металла. С другой стороны, из кристаллической структуры металлов следует, что их атомы не связаны друг с другом локализованными двухэлектронными связями, ибо числа валентных электронов атома оказывается недостаточно для образования подобных связей со всеми его соседями. Например, литий кристаллизуется в кубической объемноцентрированной решетке, и каждый его атом имеет в кристалле по 8 ближайших соседей.
Для образования двухэлектронных связей в подобной структуре атом лития должен был бы предоставить 8 электронов, что конечно, невозможно, так как он имеет лишь один валентный электрон [2].
Таким образом, в отличие от ковалентных и ионных соединений в металлах небольшое число электронов одновременно связывает большое число ядерных центров, а сами электроны могут перемещаться в металле. Иначе говоря, в металлах имеет место сильно нелокализованная химическая связь. Согласно одной из теорий металл можно рассматривать как плотноупакованную структуру из катионов, связанных друг с другом коллективизированными электронами (электронным газом).
Водородная связь
Атом водорода, ковалентно связанный с атомом сильно электроотрицательного элемента А, способен к образованию ещё одной связи с другим подобным атомом В. Эту связь называют водородной:
А—————————— δ Н………………………………………… δ-В
ковалентная водородная связь
полярная δ- связь
Чем выше электроотрицательность атомов А и В, тем больше эффективные заряды δ на атоме Н и δ- на атоме В, а следовательно, тем сильнее между ними электростатическое взаимодействие и прочнее водородная связь. Этому способствует также и расположение заряда δ- по линии, продолжающей межъядерную ось А – Н.
Протон благодаря малому размеру и сильному полю способен глубоко внедряться в электронную оболочку другого атома, поэтому в образовании водородной связи, как показывают спектральные данные, существенную роль играет также и донорно-акцепторное взаимодействие атома В как донора и атома Н как акцептора.
Для соединений фтора и кислорода характерно образование за счет водородной связи группировок из одинаковых молекул-ассоциаций (Н2О)n и (НF)m .Это сказывается на целом ряде свойств соединений и , в частности, на таких параметрах, как температуры кипения и замерзания. По относительной величине молекулярных масс Н2О и Н2S для воды tк и tз должны быть ниже, чем для сульфида водорода (-60,75 и -85,600 С). В действительности они много выше (100 и 00С ), что связано с увеличением молекулярной массы воды за счет ассоциаций её молекул. Карбоновые кислоты в жидкой и газовой фазах существуют в основном в виде димеров. В белках, нуклеиновых кислотах и других органических соединениях, имеющих большое биологическое значение, водородная связь обеспечивает поперечное сшивание цепочечных молекул. Для некоторых соединений возможно также образование внутримолекулярной водородной связи, например, в нитрофеноле.
Длина водородной связи больше длины ковалентных связей. В ряде соединений типа РА – Н…ВР’ при сокращении равновесного расстояния Н-В длина связи А-Н увеличивается и в предельном случае обе связи могут оказаться одинаковыми, как в дифторид-ионе (FНF)—.
Энергия водородной связи (8-40кДж/моль) ниже энергии ковалентных связей. Так, для льда это 20кДж/моль, что составляет 4,3 % энергии ковалентной связи Н-О, равной 456 кДж/моль. Наибольшее значение энергии водородной связи имеют соединения фтора (25-40кДж/моль) затем кислорода (13-25кДж/моль) и азота (8-21кДж/моль). Для серы и хлора образование водородных связей нехарактерно.
3.5. Молекулярное взаимодействие
Силы притяжения между молекулами, которые называют ван-дер-ваальсовыми, обусловливаются тремя видами межмолекулярного взаимодействия:
1. Ориентационное – проявляется между полярными молекулами, стремящимися занять такое положение, при котором их диполи были бы обращены друг к другу разноименными полюсами, а векторы моментов этих диполей были бы ориентированы по одной прямой;
2. Индукционное – возникает между индуцированными диполями, причиной образования которых является взаимное поляризация атомов двух сближающихся молекул;
3. Дисперсионное – возникает в результате взаимодействия микродиполей, образующихся за счет мгновенных смещений положительных и отрицательных зарядов в молекулах при движении электронов и колебаний ядер. Дисперсионные силы действуют между любыми частицами. Ориентационное и индукционное взаимодействие для частиц многих веществ, например, Не, Аr, H2 ,N2 ,CH4 не существует. Для молекул NH3 на дисперсионное взаимодействие приходится 50% , на ориентационное – 44,6% и на индукционное – 5,4%. Полная энергия ван-дер-ваальсовых сил притяжения характеризуется невысокими значениями. Так, для льда она составляет 11кДж/моль, т.е. 2,4% энергии ковалентной связи Н – О (456 кДж/моль). С ростом относительных молекулярных масс силы межмолекулярного взаимодействия становятся больше, поэтому повышаются значения таких постоянных, как температуры плавления и кипения.
Пример 1.Какую ковалентность может проявлять бром в своих соединениях?
Решение. В атоме брома распределение электронов внешнего энергетического уровня по орбиталям следующее:
| 4s | 4p | 4d | 4s | 4p | 4d | ||||||||||||||
| 35Br | ↑↓ | ↑↓ | ↑↓ | ↑ | 35Br | ↑↓ | ↑↓ | ↑ | ↑ | ↑ | |||||||||
| 4s2 | 4p2x | 4p2y | 4p2z | 4s2 | 4p2x | 4py | 4pz | 4dxy |
Ковалентность брома равна 1 (число неспаренных ē). Но бром может проявлять и большую ковалентность, а именно 3 и выше, при возбуждении. У атомов брома есть свободные α-орбитали на 4-ом энергетическом уровне. Если, например, один из электронов 4-го энергетического уровня перейдет с p-орбитали на α-орбиталь, то ковалентность брома будет равной 3. Аналогичным образом объясняется ковалентность 5 и 7.
Пример 2. Какая гибридизация электронных облаков имеет место в атоме кремния при образовании молекулы SiCl4? Какова пространственная структура этой молекулы?
Решение. В возбужденном состоянии структура внешнего энергетического уровня атома кремния 3s1 3px1 3py1 3pz1.
В образовании химических связей в атоме кремния участвуют один электрон в 3s- и три электрона в 3p-состоянии. При образовании молекулы SiCl4 возникает 4 гибридных электронных облака (sp3-гибридизация). Молекула SiCl4 имеет пространственную тетраэдрическую конфигурацию.
Пример3. Объяснить механизм образования молекулы SiF4 и SiF62- . Может ли существовать ион СF62- ?
Решение. Электронная конфигурация атома кремния 1s2 2s2 2p6 3s2 3p2. Электронное строение его валентных орбиталей в невозбужденном состоянии может быть представлено следующей графической схемой:
При возбуждении атом кремния переходит в состояние 1s2 2s2 2p6 3s1 3p3, а электронное строение его валентных орбиталей соответствует схеме:
Четыре неспаренных электрона возбужденного атома могут участвовать в образовании четырех ковалентных связей по обычному механизму с атомами фтора (1s2 2s2 2p5), имеющими по одному неспаренному электрону, с образованием молекулы SiF4 .
Для образования иона SiF62- к молекуле SiF4 должны присоединяться два иона F (1s2 2s2 2p6), все валентные электроны, которые спарены. Связь осуществляется по донорно-акцепторному механизму за счет пары электронов каждого из фторид-ионов и двух вакантных 3 α-орбиталей атома кремния.
Углерод (1s2 2s2 2p6) может образовать, подобно кремнию, соединение SF4, но при этом валентные возможности углерода будут исчерпаны (нет неспаренных электронов, неподелённых пар электронов и вакантных орбиталей на валентном уровне). Ион СF62- образоваться не может.
Пример 3. Как изменяется прочность связи H-Э в ряду H2O – Н2S – H2Se – H2Te?
Решение. В указанном ряду размеры валентных электронных облаков элементов (O, S, Se, Te) возрастают, что приводит к уменьшению степени их перекрывания с электронным облаком атома водорода и к возрастающему удалению области перекрывания от ядра атома соответствующего элемента. Это вызывает ослабление притяжения ядер взаимодействующих атомов к области перекрывания электронных облаков, т.е. ослабление связи. Таким образом, при переходе от кислорода к теллуру прочность связи H–Э уменьшается.
§
Химическое превращение есть качественный скачок, при котором исчезают одни вещества и образуются другие. Происходящая при этом перестройка электронных структур атомов, ионов и молекул сопровождается выделением или поглощением тепла, света, электричества и т.п. – превращением химической энергии в другой вид энергии.
Энергетические эффекты реакций изучает термохимия. Данные об энергетических эффектах реакций используются для расчетов тепловых балансов технологических процессов, для определения энергии межатомных и межмолекулярных связей, для выяснения строения и реакционной способности соединений, для установления направления химических процессов и т.д.
Химические реакции обычно протекают при постоянном давлении (например, в открытой колбе) или при постоянном объёме (например, в автоклаве). Процессы, протекающие при постоянном давлении, называют изобарными, а при постоянном объёме- изохорными.
Состояние системы описывается с помощью ряда переменных: давления, объёма, температуры, массы, энергии. На основе этих параметров могут быть выведены другие переменные, позволяющие характеризовать состояние системы и происходящие в ней изменения. Среди последних важное значение для химиков имеют внутренняя энергия U, энтальпия H, энтропияS, изобарный потенциал G и др.
4.1.1. Термохимия. Закон Гесса
Термохимия изучает тепловые эффекты химических процессов. Уравнения реакций, в которых учитываются их тепловые эффекты, называют термохимическими. В этих уравнениях выделение теплоты обозначают знаком ( ), а поглощение – (–), например:
H2(г) Сl2(г) = 2HСl(г) 183,6 кДж или
1/2H2 (г) 1/2Сl2(г)= HCl (г) 91,8 кДж∙моль-1
N2 (г) О2(г)= 2NО(г) – 180,4 кДж или
1/2N2 (г) О2(г)= NО(г) – 90,2 кДж∙моль-1
В термодинамике принята обратная система знаков, и выделение теплоты в результате химической реакции обозначают знаком ( — ), а поглощение теплоты- знаком ( ).
Теплотой образования называют теплоту, которая поглощается или выделяется при образовании химического соединения количеством вещества 1 моль из простых веществ при заданных условиях; теплотой разложения — теплоту, которая поглощается или выделяется при разложении химического соединения количеством вещества 1 моль на простых вещества; теплотой сгорания — теплоту, которая выделяется при сгорании вещества 1 моль.
Согласно закону Лавуазье-Лапласа теплотой разложения сложного вещества равна теплоте его образования из простых веществ, что является частным случаем закона сохранения энергии ΔU
В качестве стандартных условий в термодинамике принимается температура 2 0С
(298 К) и давление 1,013∙105 Па. Теплоты образования в этих условиях называют стандартными, для многих веществ они приводятся в таблицах справочной литературы.
Тепловые эффекты химических реакций связаны с изменением внутренней энергии системы при переходе от исходных веществ к продуктам реакции.
Внутренняя энергия (U) – это весь запас энергии системы, кроме потенциальной энергии, её положения и кинетической энергии всей системы в целом. Таким образом, U слагается из поступательного и вращательного движений молекул, колебательного движения атомов и атомных групп в молекуле, движения электронов в атомах, ядерной энергии и т.д.
Если сиcтема поглощает из внешней среды теплоту Q, то внутренняя энергия U1 увеличивается на эту величину за вычетом той её части, которая расходуется на работу, совершаемую системой (А), т.е. U2 =U1 Q-A или ΔU =Q-A , где ΔU= U2 -U1 .
Если в ходе процесса объём системы остается постоянным, т.е. работа расширения системы не совершается, то изменение внутренней энергии равно теплоте, поглощенной системой в условиях постоянного объёма: ΔU =Qv. Индексом V обозначают постоянство объёма. Изменение внутренней энергии ΔU, а следовательно, и Qv не зависит от пути процесса, что вытекает из закона сохранения энергии.
В химической практике чаще используют процессы, протекающие при постоянном давлении, когда объём системы может увеличиться на ΔV, в результате она совершит работу, равную рΔV. В этом случае процесс характеризуется энтальпией- величиной, которая определяется уравнением Н= U pΔV. Изменение энтальпии Δ Н= ΔU pΔV.
При стандартных условиях ΔН обозначают символом ΔН0298 .Для экзотермических реакций ΔН имеет отрицательные , а для эндотермических –положительные значения.
Если в ходе процесса при постоянном давлении системой совершается только работа расширения (А=рΔV), то ΔU= ΔН –pΔV или ΔU= ΔН – A, а так как ΔU=Q – A, то в этих условиях ΔН=Qp (индекс ”p” указывает постоянство давления). Так как ΔН не зависит от пути процесса, то этим свойством обладает и Qp.
Если реакция протекает в конденсированной системе, т.е. с участием только жидких и твердых веществ, то изменение объёма ΔV практически равно нулю. Тогда pΔV=0, и следовательно, ΔН=ΔV. В этом случае тепловые эффекты реакций при постоянном давлении и постоянном объёме практически равны между собой: Qv =Qр .
Поэтому при термохимических расчетах для конденсированных систем ограничивающие условия р= const или V= const опускаются.
Основным законом термохимии является закон Гесса (1840): тепловой эффект химических реакций, протекающих при постоянном объёме или при постоянном давлении, не зависит от числа промежуточных стадий и определяется только начальным и конечным состоянием системы.
Закон Гесса можно иллюстрировать схемой образования СО2: ΔН=ΔН1 ΔН2,
С ΔН СО2
ΔН1 ΔН2
СО
т.е. тепловой эффект реакции равен сумме тепловых эффектов отдельных стадий. Из закона Гесса следует, что теплота образования вещества не зависит от способов его получения.
Следствие закона Гесса: стандартный тепловой эффект реакции равен сумме стандартных теплот образования продуктов реакции за вычетом суммы стандартных теплот образования исходных веществ:
ΔН0298(реакции)=∑ ΔН0298(прод.) -∑ΔН0298(исх.).
При термохимических расчетах энтальпии образования простых веществ (Н2, Сl2 и др.) в стандартном состоянии принимаются равными нулю. Поэтому тепловой эффект реакции синтеза соединений из простых веществ равен стандартной теплоте их образования. Например, для реакции
Н2(г) Вr2(г) → 2HВr(г) ΔН0298=2(-36,3)- (0 0)= -72,6 кДж,
т.е. тепловой эффект равен удвоенной стандартной теплоте образования НВr и реакция является экзотермической.
Закон Гесса позволяет также рассчитывать теплоты образования нестабильных соединений и тепловые эффекты реакций, которые нельзя осуществить экспериментально. Так, невозможно определить тепловой эффект реакции горения графита до оксида СО, т.к. при этом всегда образуется то или иное количество СО2 .Однако, тепловой эффект этой реакции может быть найден по экспериментально определенным теплотам сгорания графита до СО2 и сгорания CO до СО2:
С О2 → СО2 ΔН =-393,5 кДж/моль
СО 1/2О2→ CО2 ΔН1 =-283,0 кДж/моль
С 1/2О2→ СО ΔН2 = ?
Согласно закону Гесса ΔН= ΔН1 ΔН2, откуда ΔН2 = ΔН — ΔН1 = — 393,5 – (-283,0) = -110,5 кДж/моль.
Энтропия
Большинство процессов представляет собой два одновременно происходящих явления: передачу энергии и изменение в упорядоченности расположения частиц друг относительно друга.
Частицам (молекулам, атомам, ионам) присуще стремление к беспорядочному движению, поэтому система стремится перейти их более упорядоченного состояния в мене упорядоченное. Количественной мерой беспорядка является энтропия S. Изменение энтропии ΔS в изолированной системе, переходящей из состояния 1 в состояние 2, можно определить соотношением
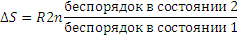
где R- газовая постоянная.
Если, например, баллон с газом соединить с вакуумированным сосудом, то газ из баллона будет распределяться по всему объёму сосуда. При этом система из более упорядоченного состояния (с меньшим беспорядком) переходит в состояние менее упорядоченное (с большим беспорядком). Таким образом, при переходе системы из более упорядоченного состояния в менее упорядоченное состояние энтропия возрастает.
Переход же системы из менее упорядоченного состояния в более упорядоченное состояние связан с уменьшением энтропии, и самопроизвольное протекание подобного процесса менее вероятно. Так, ясно, что в рассматриваемом примере система самопроизвольно не может перейти из состояния 2 в состояние 1, т.е. невероятно, чтобы газ сам собой собрался в баллоне. В случае перехода системы из менее упорядоченного состояния в более упорядоченное ΔS системы — величина отрицательная, т.е. энтропия S системы уменьшается.
Энтропия возрастает при переходе жидкости в пар, при растворении кристаллического вещества и т.д. В процессах конденсации и кристаллизации вещества энтропия уменьшается. Энтропия вещества в газовом состоянии значительно больше, чем в жидком, а тем более, чем в твердом.
Энтропии веществ, как и их теплоты образования, принято относить к определенным условиям, обычно при температуре 25 0С (298 К) и давления 1 атм. Энтропию при этих условиях обозначают S0298 и называют стандартной энтропией.
Значениями энтропии веществ пользуются для установления изменения энтропии системы в результате соответствующих процессов. Так, для химической реакции
аА bB …= dD еЕ …изменение энтропии системы будет
ΔS= (dSD eSE …)-( aSA bSB …) или ΔS= ∑Sпрод. — ∑Sисх.
Об изменении энтропии в химических реакциях можно судить по изменению объёма системы в ходе реакции. Например, в реакции ½ С (графит) ½ СО2(г)=СО(г) наблюдается увеличение объёма ΔV>0; следовательно, энтропия возрастает ΔS> 0 (ΔS0298=87,7 дж/моль∙град). В случае же реакции образования Н3N из водорода и азота 3/2 Н2 (г) 1/2 N2 (г)= H3N(г) наоборот, объём системы уменьшается ΔV<0; следовательно, энтропия уменьшается ΔS<0 (ΔS0298=99,1дж/моль∙град).
Если же реакция протекает между твердыми веществами, например,
Аl(к) Sb(к)=АlSb(к), то изменения объёма системы и её энтропии практически не происходит (ΔS0298=4,03дж/моль∙град). То же самое относится и к процессам, в которых число молей газообразных веществ не изменяется, например, С (графит) О2 (г)= СО2 (г), ΔS=2,9дж/моль∙град.
4.1.3. Энергия Гиббса и направленность химических процессов
Возможность самопроизвольного протекания химического процесса определяется двумя факторами: стремление системы к понижению внутренней энергии за счет экзотермической реакции (-∆H) и со стремлением системы к увеличению неупорядоченности в расположении частиц за счет теплового движения, мерой которой является функция состояния, называемая энтропией S.
Если ∆H незначительно зависит от температуры, то энтропия с повышением температуры сильно возрастает. Влияние как энтальпийного так и энтропийного факторов учитывается в уравнении ∆G=∆H-T∆S. Функцию G называют энергией Гиббса, она является мерой устойчивости системы в условиях T=const и p=const.
Состояние системы при постоянном объеме описывается функцией, которую называют энергией Гельмгольца: ∆P=∆U-T∆S. Таким образом, ∆G отличается от ∆P так же, как ∆H от ∆U на величину, равную работе расширения p∆V.
Изменение энергии Гиббса ∆G определяет возможность или невозможность самопроизвольного протекания процесса. Если ∆G<0, т.е. по ходу реакции происходит уменьшение энергии Гиббса, то этот процесс термодинамически возможен. Если ∆G>0, т.е. процесс ведет к увеличению энергии Гиббса, то такая реакция термодинамически невозможна. Если ∆G=0, то реакционная система находится в состоянии равновесия.
При положительном значении ∆S и, следовательно, T∆S величина G будет отрицательной: а) при любых отрицательных значениях Н, т.е. все экзотермические процессы в этом случае возможны; б) при положительных значениях ∆Н, но при условии, что по абсолютному значению ∆Н<T∆S, т.е. эндотермические реакции возможны, когда энтропийный фактор преобладает над энтальпийным, что легче реализуется с ростом температуры.
При отрицательном значении ∆S в уравнении ∆G=∆H-T∆S величина T∆S становится положительной, поэтому в этом случае эндотермические реакции ( ∆Н) самостоятельно протекать не могут, так как ∆G будет величиной также положительной. Из экзотермических реакций (-∆Н) при таком условии возможны только те, которые характеризуются большим отрицательным значением ∆Н, т.е. те эндотермические реакции, для которых сумма -∆Н (-Т∆S) имеет отрицательное значение.
При очень низких температурах величина Т∆S минимальна, так как и энтропия в этих условиях изменяется незначительно, поэтому преимущественное влияние на направление процесса имеет энтальпийный фактор и обычно процессы идут в сторону экзотермических реакций. В конденсированных системах реакции протекают с незначительным изменением энтропии, поэтому знак ∆G определяется знаком ∆Н.
Таким образом, для определения возможности протекания процесса при данных условиях надо найти знак ∆G. С этой целью в справочных таблицах находят стандартные значения ∆Н и S для веществ, участвующих в реакции, по которым вычисляют ∆G на формулы ∆Go298=∆Ho298-T∆So298[3].
Пример 1. Расчет теплового эффекта химической реакции по теплоте образования реагирующих веществ и продуктов реакции.
Определите количество теплоты, выделяющейся при гашении 100кг извести водой при 25оС, если известны стандартные теплоты образования веществ, участвующих в химической реакции:
∆Ho298, CaO(к) = -635,1 кДж∙моль-1;
∆Ho298, H2O(ж) = -285,84 кДж∙моль-1;
∆Ho298, Ca(OН)2(к) = -986,2 кДж∙моль-1;
Решение. Реакция гашения извести: СаО(к) Н2О(ж)=Са(ОН)2(к). Согласно первому следствию из закона Гесса тепловой эффект химической реакции равен разности между суммой теплот образования реагирующих веществ с учетом стехиометрических коэффициентов:
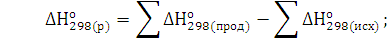
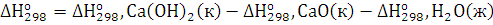 =
=
=-986,2-(-635,1)-(-285,84) = 65,26 кДж∙моль-1
Таким образом, при гашении водой 1 моль извести выделяется 65,26кДж, при гашении 1кмоль извести – 65260 кДж. М(СаО) = 56г∙моль-1=56кг∙моль-1; m(СаО) = 100кг;
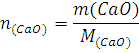
При гашении водой 100 кг извести выделяется 100/56∙65260=116536кДж.
Пример 2. Расчет теплоты образования.
Определить теплоту образования Са(ОН)2тв на основе реакций:
СаСО3→СаО СО2 ∆Н1; СаО Н2О→Са(ОН)2тв ∆Н2.
Решение. Для определения суммарной теплоты образования ∆Н для этой реакции определяем ∆Н1 и ∆Н2, тогда ∆Н=∆Н1 ∆Н2;
∆Н1=∆НСаО ∆Н(СО2)-∆НСаСО3 = 177,83 кДж∙моль-1;
∆Н2=∆НСа(ОН)2-∆НСаО-∆НН2О = -65,2 кДж∙моль-1;
∆Н= 177,83 – 65,2 = 113,61 кДж∙моль-1.
Пример 3. Рассчитайте тепловой эффект реакции горения сероводорода по следующим данным: Н2S(г) 3/2O2=Н2О(ж) SО2(г)
1)S(к) Н2 = Н2S(г); ∆Н1= -20,17 кДж
2)Н2 1/2 O2 = H2O(ж); ∆Н2= -286,0 кДж
3)S(к) О2 = SО2(г); ∆Н3= -297 кДж
Решение. Уравнение 1-3 есть термохимические уравнения образования соответсвенно 1 моль Н2S(г), Н2О(ж), SО2(г) из простых веществ в стандартных условиях: Т=298К и Р=101,325 кПа, а тепловые эффекты – стандартные энтальпии образования указанных соединений ∆Ho298. Если сложить термохимические уравнения 2 и 3 и вычесть уравнение 1, получим искомое уравнение
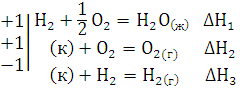
Н2S(г) 3/2 O2 = H2O(ж) SO2(г) ∆Н=∆Н1 ∆Н2-∆Н3
Подставить численное значение энтальпий образования Н2S(г) , Н2О(ж), SO2(г), получим значение теплового эффекта реакции ∆Н= -286 -297 –(-20,17) = = -562,8 кДж. Отрицательное значение энтальпии реакции горения сероводорода означает, что данная реакция экзотермическая.
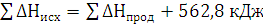
Тепловой эффект можно включить в уравнение химической реакции
Н2S(г) 3/2О2 = Н2О(ж) SO2(г) 562,8 кДж. Эта запись также представляет собой термохимическое уравнение реакции.
Пример 4. Определение изменения энтропии в стандартных условиях. Определить изменение энтропии реакции Na2O SiO2=Na2SiO3 при температуре 298К.
Решение. Находим по справочнику значения энтропии продукта и исходных веществ при Т=298К, So298, Na2O(т)=42,09Дж∙моль-1∙к-1
S o298, SiO2 (т) = 71,1Дж∙моль-1∙к-1;
S o298, Na2SiO3 (т)=113,8Дж∙моль-1∙к-1. Изменение энтропии в химической реакции равно разности между суммой энтропий продуктов реакции и суммой энтропий исходных веществ с учетом стехиометрических коэффициентов.
So298 х.р. = So298, Na2SiO3(т) – So298, SiO2 (т) — So298, Na2O(т) = 113,8-71,1-42,09=0,61 Дж∙моль-1∙к-1
Пример 5. Определение изменения энтропии при фазовых превращениях. Определить изменение энтропии 1г кристобалита при температуре плавления 1986К, если теплота обратного фазового превращения кристобалита равна 744,05 Дж∙r-1.
Решение. Изменение энтропии при переходе вещества из одного агрегатного состояния в другое равно: 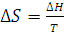 , где ∆Н-теплота обратимого фазового превращения.
, где ∆Н-теплота обратимого фазового превращения.
S2-S1=∆S= 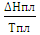 =
= 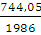 = 0,238Дж∙г-1∙град-1.
= 0,238Дж∙г-1∙град-1.
Пример 6.Вычислите 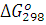 для химической реакции 2SO2(г) О2(г)↔2SO3(г). В каком направлении может протекать эта реакция в стандартных условиях?
для химической реакции 2SO2(г) О2(г)↔2SO3(г). В каком направлении может протекать эта реакция в стандартных условиях?
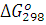 , SO2(г) = -300,37 кДж∙моль-1;
, SO2(г) = -300,37 кДж∙моль-1;
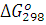 , SO3(г) = -370,37 кДж∙моль-1
, SO3(г) = -370,37 кДж∙моль-1
Решение. Изменение энергии Гиббса в химической реакции
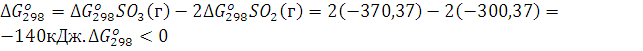 ,поэтому в стандартных условиях данная реакция может протекать в сторону образования SO3.
,поэтому в стандартных условиях данная реакция может протекать в сторону образования SO3.
§
Пример 1. При взаимодействии кристаллов хлорида фосфора (V) с парами воды образуется жидкий РОС13 и хлороводород. Реакция сопровождается выделением 111,4 кДж теплоты. Напи шите термохимическое уравнение этой реакции.
Решение. Уравнения реакций, в которых около символов химических соединений указываются их агрегатные состояния или кристаллическая модификация, а также числовое значение тепловых эффектов, называют термохимическими. В термохимических уравнениях, если это специально не оговорено, указываются значения тепловых эффектов при постоянном давлении Qp, равные изменению энтальпии системы ∆Н. Значение ∆Н приводят обычно в правой части уравнения, отделяя его запятой или точкой с запятой. Приняты следующие сокращенные обозначения агрегатного состояния вещества: г — газообразное, ж — жидкое, к — кристаллическое. Эти символы опускаются, если агрегатное состояние веществ очевидно.
Если в результате реакции выделяется теплота, то ∆Н < 0. Считывая сказанное, составляем термохимическое уравнение анной в примере реакции:
РС15(к) Н2О(г) = РОСl 3(ж) 2НС1(г); ∆Нхр = -111,4 кДж
Таблица 3
Стандартные теплоты (энтальпии) образования  некоторых веществ
некоторых веществ
| Вещество | Состо- яние | ∆Н 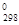 , кДж/моль , кДж/моль | Вещество | Состо-яние | ∆Н 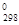 , кДж/моль , кДж/моль |
| С2Н2 СS2 NО С6Н6 С2Н4 Н2S NН3 СН4 С2Н6 НСl | г г г г г г г г г г | 226,75 115,28 90,37 82,93 52,28 -20,15 -46,19 -74,85 -84,62 -92,31 | СО СН3ОН С2Н5ОН Н2О Н2О NН4Сl СО2 Fе2О3 ТiО2 Са(ОН)2 Аl2О3 | г г г г ж к г к к к к | -110,52 -201,17 -235,31 -241,83 -285,84 -315,39 -393,51 -822,10 -943,90 -986,50 -1669,80 |
Пример 2. Реакция горения этана выражается термохимическим уравнением С2Н6(г) 3 ½ О2 = 2 СО2(г) 3 Н2О(ж); Нхр = -1559,87 кДж.
Вычислите теплоту образования этана, если известны теплоты образования СО2(г) и Н2О(ж) (см. табл. 5 ).
Решение. Теплотой образования (энтальпией) данного соединения называют тепловой эффект реакции образования 1 моль этого соединения из простых веществ, взятых в их устойчивом состоянии при данных условиях. Обычно теплоту образования относят к стандартному состоянию, т.е. 25 оС (298 К) и 1,013∙105 Па и обозначают через ∆Н 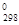 . Так как тепловой эффект с температурой изменяется незначительно, то в дальнейшем индексы опускаются и тепловой эффект обозначается через ∆Н. Следовательно, нужно вычислить тепловой эффект реакции, термохимическое уравнение которой имеет вид
. Так как тепловой эффект с температурой изменяется незначительно, то в дальнейшем индексы опускаются и тепловой эффект обозначается через ∆Н. Следовательно, нужно вычислить тепловой эффект реакции, термохимическое уравнение которой имеет вид
2С (графит) ЗН2(г) — С2Н6(г); ∆Н= ?
исходя из следующих данных:
а) С2Н6(г) 3’/2О2(г) = 2СО2(г) ЗН2О(ж); ∆Н= -1559,87 кДж;
б) С (графит) О2(г) = СО2(г); ∆Н = -393,51 кДж;
в) Н2(г) ½ O2 = Н2О(ж); ∆Н = — 285,84 кДж.
На основании закона Гесса с термохимическими уравнениями можно оперировать так же, как и с алгебраическими. Для получения искомого результата следует уравнение (б) умножить на 2, уравнение (в) — на 3, а затем сумму этих уравнений вычислить из уравнения (а):
С2Н6 372О2 — 2C — 2О2-ЗН2 —3/2О2 = 2СО2 ЗН2О -2СО2 — ЗН2О
∆Н = -1559,87 -2(-393,51)-3(-285,84) = 84,67 кДж;
∆Н = -1559,87 787,02 857,52; С2Н6 = 2С ЗН2; ∆Н= 84,67 кДж.
Так как теплота образования равна теплоте разложения с обратным знаком, то ∆Н  (г) = -84,67 кДж . К тому же результату придем, если для решения задачи применить вывод из закона Гесса:
(г) = -84,67 кДж . К тому же результату придем, если для решения задачи применить вывод из закона Гесса:
∆Нхр = 2∆НСО2 З∆НН2О — ∆НС2н6 — 3 ½ ∆НО2
Учитывая, что теплоты образования простых веществ условно приняты равными нулю ∆Нс2н6 = 2∆НСО  З∆НН
З∆НН  О — ∆Нхр
О — ∆Нхр
∆Нс2н6 = 2(-393,51) 3(-285,84) 1559,87 = -84,67;
то ∆Н 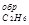 (г) = -84,67 кДж
(г) = -84,67 кДж
Пример 3. Реакция горения этилового спирта выражается термохимическим уравнением
С2Н5ОН(ж) ЗО2(г) = 2СО2(г) ЗН2О(ж); ∆Н= ?
Вычислите тепловой эффект реакции, если известно, что молярная теплота парообразования С2Н5ОН(ж) равна 42,36 кДж, а теплоты образования С2Н5ОН(г), СО2(г), Н2О(ж) см. табл. 5.
Решение. Для определения ∆Н реакции необходимо знать теплоту образования С2Н5ОН(ж). Последнюю находим из данных:
С2Н5ОН(ж) = С2Н5ОН(г); ∆Н= 42,36 кДж 42,36=-235,31-∆НС2Н5ОН (ж);
∆НС2Н5ОН (ж) = -235,31 — 42,36 = -277,67 кДж.
Вычисляем реакции, применяя следствия из закона Гесса:
∆Нхр = 2(-393,51) 3(-285,84) 277,67 = -1366,87 кДж.
Пример 4. В каком состоянии энтропия 1 моль вещества больше при одинаковой температуре: в кристаллическом или парообразном?
Решение. Энтропия есть мера неупорядоченности состояния вещества. В кристалле частицы (атомы, ионы) расположены упорядоченно и могут находиться лишь в определенных точках пространства, а для газа таких ограничений нет. Объем 1 моль газа гораздо больше объема 1 моль кристаллического вещества; возможность хаотичного движения молекул газа больше. А так как энтропию можно рассматривать как количественную меру хаотичности атомно-молекулярной структуры вещества, то энтропия 1 моль паров вещества больше энтропии 1 моль его кристаллов при одинаковой температуре.
Пример 5. Прямая или обратная реакция будет протекать при стандартных условиях в системе СН4(г) СО2 2СО(г) 2Н2(г)
2СО(г) 2Н2(г)
Решение. Вычислим ∆G  прямой реакции. Значения ∆G
прямой реакции. Значения ∆G  соответствующих веществ приведены в таблице 4. Зная, что ∆G есть функция состояния и что ∆G для простых веществ, находящихся в устойчивых при стандартных условиях агрегатных состояниях, равны нулю, находим ∆G
соответствующих веществ приведены в таблице 4. Зная, что ∆G есть функция состояния и что ∆G для простых веществ, находящихся в устойчивых при стандартных условиях агрегатных состояниях, равны нулю, находим ∆G  процесса: ∆G
процесса: ∆G  = 2(-137,27) 2(0) — (-50,79 — 394,38) = 170,63 кДж.
= 2(-137,27) 2(0) — (-50,79 — 394,38) = 170,63 кДж.
То что ∆G 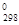 > 0, указывает на невозможность самопроизвольного протекания прямой реакции при Т = 298К и давлении взятых газов равном 1,013 *105 Па (760 мм рт. ст. = 1 атм).
> 0, указывает на невозможность самопроизвольного протекания прямой реакции при Т = 298К и давлении взятых газов равном 1,013 *105 Па (760 мм рт. ст. = 1 атм).
Таблица 4
Стандартная энергия Гиббса образования 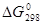 некоторых веществ
некоторых веществ
| Вещество | Состояние | 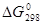 , ,кДж/моль | вещество | Состояние | 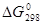 кДж/моль |
| ВаSО4 | К | -1138,8 | FeO | К | -244,3 |
| СаСО3 | К | -1128,75 | H2O | Ж | -237,19 |
| Fе3О4 | К | -1014,2 | H2O | Г | -228,59 |
| ВеСО3 | К | -944,75 | PbO2 | К | -219,0 |
| СаО | К | -604,2 | CO | Г | -137,27 |
| ВеО | К | -581,61 | CH4 | Г | -50,79 |
| NаF | К | -541,0 | NO2 | Г | 51,84 |
| ВаО | К | -528,4 | NO | Г | 86,69 |
| СО2 | Г | -394,38 | C2H2 | Г | 209,20 |
| NaCl | К | -384,03 | |||
| ZnO | К | -318,2 |
Таблица 5
Стандартные абсолютные энтропии 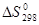 некоторых веществ
некоторых веществ
| Вещество | Состоя ние | 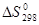 Дж/ Дж/(моль∙К) | вещество | Состоя ние | 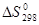 Дж/(моль∙К) Дж/(моль∙К) |
| С | алмаз | 2.44 | H2O | Г | 188,72 |
| С | Графит | 5.69 | N2 | Г | 191,49 |
| Fe | К | 27.2 | NH3 | Г | 192,50 |
| Ti | К | 30.7 | CO | Г | 197,91 |
| S | Ромб | 31.9 | C2H2 | Г | 200,82 |
| TiO2 | К | 50.3 | O2 | Г | 205,03 |
| FeO | К | 54.0 | H2S | Г | 205,64 |
| H2O | Ж | 69.94 | NO | Г | 210,20 |
| Fe2O3 | К | 89.96 | CO2 | Г | 213,65 |
| NH4Cl | К | 94.5 | C2H4 | Г | 219,45 |
| CH3OH | Ж | 126.8 | Cl2 | Г | 222,95 |
| H2 | Г | 130.59 | NO2 | Г | 240,46 |
| Вещество | Состоя ние | 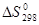 Дж/ Дж/(моль∙К) | вещество | Состоя ние | 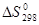 Дж/(моль∙К) Дж/(моль∙К) |
| Fe3O4 | К | 146.4 | PCl3 | Г | 311,66 |
| CH4 | Г | 186.19 | PCl5 | Г | 352,71 |
| HCl | Г | 186.69 |
Пример 6. На основании стандартных теплот образования (см. табл. 3) и абсолютных стандартных энтропии веществ (табл. 5) вычислите ∆S 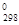 реакции, протекающей по уравнению СО(г) Н2О(ж) = СО2(г) Н2(г)
реакции, протекающей по уравнению СО(г) Н2О(ж) = СО2(г) Н2(г)
Решение. ∆G0= ∆Н — Т∆S0; ∆Н и ∆S — функции состояния, поэтому
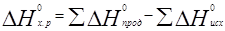
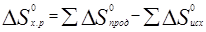
∆Н 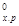 = (-393,51 0) – (-110,52-285,84) = 2,85 кДж
= (-393,51 0) – (-110,52-285,84) = 2,85 кДж
∆S 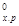 =(213.65 130.59) – (197.91 69.94) = 79.39 = 0.07639кДж/ (моль∙К)
=(213.65 130.59) – (197.91 69.94) = 79.39 = 0.07639кДж/ (моль∙К)
∆G0 = 2,85 – 298 ∙ 0,07639 = — 19,91 кДж
Пример 7.Реакция восстановления Fe2O3 водородом протекает по уравнению Fe2O3(к) 3H2(г) = 2Fe(к) ЗН2О(г); ∆Н= 96,61 кДж
Возможна ли эта реакция при стандартных условиях, если изменение энтропии ∆S = 0,1387 кДж/(моль∙К)? При какой температуре начнется восстановление Fe2О3?
Решение. Вычисляем ∆G0 реакции: ∆G =∆H-T∆S = 96,61 -298 ∙ 0,1387 = 55,28 кДж.
Так как ∆G > 0, то реакция при стандартных условиях невозможна; наоборот, при этих условиях идет обратная реакция окисления железа (коррозия). Найдем температуру, при которой ∆G =0
∆Н = Т∆S; 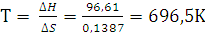
Следовательно, при температуре ≈ 696,5 К начнется реакция восстановления Fe2O3. Иногда эту температуру называют температурой начала реакции.
Пример 8.Вычислите ∆Н°, ∆S и ∆G  реакции, протекающей по уравнению Fe2O3(к) ЗС = 2Fe ЗСО Возможна ли реакция восстановления Fe2O3 углеродом при 500 и 1000 К?
реакции, протекающей по уравнению Fe2O3(к) ЗС = 2Fe ЗСО Возможна ли реакция восстановления Fe2O3 углеродом при 500 и 1000 К?
Решение. ∆Н 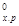 и ∆S
и ∆S 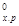 находим из соотношений (1) и (2):
находим из соотношений (1) и (2):
∆Н 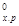 = [3(-110.52) 2∙0]-[-822.10 3∙0]
= [3(-110.52) 2∙0]-[-822.10 3∙0]
Энергию Гиббса при соответствующих температурах находим из соотношения
∆G500= 490,54 -500 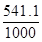 = 219,99кДж
= 219,99кДж
∆G1000 = 490,54 — 1000 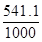 = -50.56кДж
= -50.56кДж
Так как ∆G500 >0, а ∆G1000 <0, то восстановление Fe2O3 возможно при 1000 К и невозможно при 500К.
§
Изучение скоростей реакции позволяет выяснить истинный механизм протекания сложных химических превращений. Это в свою очередь создает перспективы для нахождения путей управления химическим процессом, т.е. его скоростью и направлением. Выяснение кинетики реакций позволяет осуществить математическое моделирование реакций, происходящих в химических аппаратах, и с помощью электронно-вычислительной техники решать задачи оптимизации и автоматизации химико-технологических процессов.
Реакции могут быть гомогенными и гетерогенными. Гомогенные реакции протекают в однородной среде (например, в газовой фазе или жидком растворе). Гетерогенные реакции протекают в неоднородной среде – между веществами, которые находятся в разных фазах (твердой и жидкой, газовой и жидкой и т.д.). Таким образом, гомогенные реакции происходят равномерно во всем объеме, заполненном реагентами, гетерогенные — только на некоторых пограничных поверхностях — на границе раздела фаз. Примером гетерогенной реакции может служить реакция между веществом в газовой фазе и поверхностью жидкого или твердого тела.
Скоростью реакции называется число элементарных актов реакции, происходящих в единицу времени в единице объема (в случае гомогенных реакций) или на единице поверхности раздела фаз (в случае гетерогенной реакции). Скорость реакции обычно характеризуют изменением концентрации какого-либо из исходных или конечных продуктов реакции в единицу времени и чаще всего выражают в моль/см3*мин.
О скорости реакции можно судить также по скорости изменения какого-либо свойства системы, например, окраски, электрической проводимости, давления, спектра и т.д.
Если в момент времени τ1 и τ2 концентрации одного из исходных веществ равны с1 и с2, то среднюю скорость υ в интервале времени τ1 и τ2 можно выразить как:
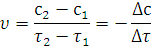
Поскольку речь идет об убыли концентрации исходного вещества, изменение концентрации в этом случае берется со знаком минус.
В ходе химических процессов концентрации веществ меняются непрерывно. Поэтому важно знать скорость реакции в данный момент времени, т.е. мгновенную скорость реакции. Последняя выражается первой производной концентрации по времени:
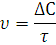
Если скорость реакции оценивается увеличением концентрации одного из продуктов реакции, то производная берется со знаком плюс.
Скорость химических превращений зависит от природы реагирующих веществ, их концентраций и внешних условий.
Скорость гомогенных реакций зависит от концентрации реагирующих веществ. Скорость реакции пропорциональна произведению концентраций реагирующих веществ, возведенных в степени их стехиометрическим коэффициентом.
Указанная закономерность называется законом действующих масс(Гульдберг и Вааге).
 Для двухмолекулярной реакции взаимодействия водорода и йода Н2(г) I2(г)=2НI(г) закон действующих масс выражается в виде следующего кинетического уравнения: ,
Для двухмолекулярной реакции взаимодействия водорода и йода Н2(г) I2(г)=2НI(г) закон действующих масс выражается в виде следующего кинетического уравнения: ,
где υ-скорость реакции; [Н2] и [I2] – концентрации соответственно Н2 и I2. Кинетическое уравнение для трехмолекулярной реакции 2NO(г) Cl2(г) = 2NOCl (г) будет 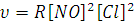
Коэффициент пропорциональности R называется константой скорости реакции. Величина R численно равна скорости реакции, когда концентрации реагирующих веществ равны единице. Константа скорости реакции зависит от: 1)природы реагирующих веществ; 2)температуры; 3)давления; 4)концентрации; 5)катализаторов.
Зависимость скорости реакции от температуры определяется правилом Вант-Гоффа, согласно которому
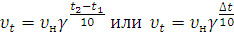
где υt — скорость реакции при температуре t2, до которой нагревалась или охлаждалась система; υн – скорость реакции при начальной температуре t1; ∆t=t2-t1 и γ – температурный коэффициент, т.е. число, показывающее, во сколько раз увеличивается скорость реакции при повышении температуры на каждые 10о. Значения γ при обычных температурах лежат в пределах 2-4 для большинства реакций.
Увеличение скорости реакции с повышением температуры объясняется увеличением числа так называемых активных молекул, т.е. молекул, обладающих достаточной энергией для осуществления химического взаимодействия при их столкновении. Та минимальная избыточная энергия по сравнению со средней энергией, которой должны обладать молекулы, чтобы реакция между ними стала возможной, называется энергией активации Еа.
Разница между средней энергией молекул продуктов реакций и молекул исходных веществ (Ек-Ен) определяют тепловой эффект реакции 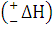 . Если Ек<Ен, то процесс будет экзотермическим, а если Ек>Ен, то процесс будет экзотермическим, а если Ек>Ен, то эндотермическим.
. Если Ек<Ен, то процесс будет экзотермическим, а если Ек>Ен, то процесс будет экзотермическим, а если Ек>Ен, то эндотермическим.
4.2.2. Физические методы стимулирования химических превращений
В связи с поисками новых путей проведения процессов в химической технологии разрабатываются методы направленного регулирования реакционной способности веществ и весьма интенсивно изучаются процессы, протекающие при различных физических воздействиях на вещество. Кроме нагревания на реакционную способность веществ существенное влияние оказывают свет, ионизирующие излучения, давление, механическое воздействие и др.
Воздействие света (видимого, ультрафиолетового) на реакции изучает особый раздел химии — фотохимия. Фотохимические процессы весьма разнообразны. К ним относятся некоторые реакции синтеза (хлорида водорода, органических веществ в растениях); разложения (перекиси водорода, светочувствительных материалов) и др. Фотохимическое действие света заключается в том, что молекулы реагирующих веществ, поглощая кванты света, возбуждаются, т.е. становятся реакционноспособными или распадаются на ионы и свободные радикалы.
Существенно новым способом воздействия на вещество является использование лазерного излучения. Его действие может быть фотохимическим и чисто термическим. Лазерное излучение обладает рядом уникальных свойств, которых лишены обычные источники света. Наиболее важным его свойством, с точки зрения применения для фотохимического инициирования химических реакций, является извлечение мощных потоков световой энергии в узких спектральных интервалах. Поэтому, используя излучение определенной длины волны, поглощаемое реагентом, но не поглощаемое примесями, можно осуществить избирательную реакцию.
Рентгеновские лучи, альфа-частицы, гамма-лучи, нейтроны и другие излучения большой энергии вызывают в веществе глубокие физико-химические изменения и инициируют разнообразные реакции. Так, при действии ионизирующих излучений на кислород образуется озон, алмаз превращается в графит, оксиды марганца выделяют кислород и т.д. При действии ионизирующих излучений на воду происходит ее радиолиз.
Химические процессы, происходящие под действием ионизирующих излучений, изучает радиационная химия. Радиационно-химические реакции используются для синтеза высокомолекулярных органических веществ и для изменения их структуры. По мере освоения атомной энергетики радиационная химия все шире проникает в химическую промышленность.
Химические превращения, происходящие под действием механических сил, изучает механохимия. Элементарным механохимическим актом является разрыв химических связей в веществе под действием механических сил (вальцевание, дробление, перетирание и др.).
Еще более сильные изменения претерпевают вещества под действием сверхвысоких давлений (порядка десятков тысяч атмосфер). Пример тому — образование более плотных и более твердых модификаций вещества, например превращение графита в алмаз.
Большое развитие получила химия ударного сжатия. При сжатии твердых тел и жидкостей ударными волнами, образуемыми, например, детонацией взрывчатых веществ, при взрывах, в миллионные доли секунды развиваются в веществе давления в десятки и сотни атмосфер, скачком изменяются плотность и температура вещества. При этом образуются активные частицы как радикального, так и ионного типов. Последствия прохождения через вещество ударной волны могут быть самыми различными. Взрыв, с одной стороны, вызывает раздробление вещества, распад сложного вещества на относительно более простые. Но возможно и обратное превращение – образование из простых молекул более сложных и длинных полимерных цепей [4].
Катализ
Одним из наиболее распространенных в химической практике методов ускорения химических реакций является катализ. В присутствии катализаторов изменяется путь, по которому проходит суммарная реакция, а потому изменяется ее скорость. Катализаторы — это вещества, изменяющие скорость реакции за счет участия в промежуточном химическом взаимодействии с компонентами реакции, но восстанавливающие после каждого цикла промежуточного взаимодействия свой химический состав. Увеличение скорости катализируемой реакции связано с меньшей энергией активации нового пути реакции.
Изменение скорости катализируемой реакции за с чет снижения энергии активации ее отдельных стадий можно рассмотреть на следующем примере. Допустим, между веществами А и В возможно взаимодействие с образованием соединения АВ (∆G < 0):
А В → А…В → АВ
Но в силу высокой энергии активации эта реакция протекает с очень малой, практически равной нулю скоростью. Пусть, найдено такое третье вещество К (катализатор), которое легко вступает во взаимодействие с А (в силу другой природы реагирующих веществ, а следовательно, другой, меньшей, энергии активации), образуя соединение АК:
А К → А…К → АК
Соединение же АК легко взаимодействует с веществом В (опять-таки в силу иной природы веществ и малой энергии активации), образуя вещества АВ и К:
В АК → В…АК → АВ К
Суммируя два последних уравнения, получим А В = АВ т.е. в результате реакции катализатор остался без изменения.
Пример 1. Вычисление скорости реакции по концентрациям реагирующих веществ.
Реакция между веществами А и В протекает по уравнению 2А В=С; концентрация вещества А равна 6 моль∙л-1, а вещества В-5 моль∙л-1. Константа скорости реакции равна 0,5л2∙моль-2 с-1. Вычислите скорость химической реакции в начальный момент и в тот момент, когда в реакционной системе останется 45% вещества В.
Решение. Скорость химической реакции выражается уравнением υ=k[A]2[B]. Скорость химической реакции в начальный момент равна υ1=0,5∙62∙5=90,0 моль∙с-1∙л-1. Через некоторое время в реакционной смеси останется 45% вещества В, т.е. концентрация вещества В станет 5∙0,45=2,25моль∙л-1. Следовательно, концентрация вещества В уменьшилась на 5,0-2,25=2,75 моль∙л-1, а концентрация вещества А уменьшилась на 5,5 моль∙л-1 и стала равной 0,5моль∙л-1 (6-5,5). Отсюда υ2=0,5∙(0,5)2∙2,25=0,28 моль∙с-1∙л-1.
Пример 2. Влияние давления на скорости реакции.
Определите, как изменится скорость прямой реакции 2СО О2=2СО2, если общее давление в системе увеличить в 4 раза.
Решение. При увеличении давления в 4 раза объем системы уменьшится в 4 раза, а концентрация реагирующих веществ возрастет в 4 раза. Тогда υ1=k[CO]2[O2], а υ2= k[4CO]2[4O2]; 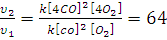
§
Большинство химических реакций обратимы, т.е. протекают одновременно в противоположных направлениях. В тех случаях, когда прямая и обратная реакции идут с одинаковой скоростью, наступает химическое равновесие. Например, в обратимой гомогенной реакции: H2(г) I2(г) ↔ 2HI(г) соотношение скоростей прямой и обратной реакций согласно закону действующих масс зависит от соотношения концентраций реагирующих веществ, а именно: скорость прямой реакции: υ1 = k1[Н2][I2]. Скорость обратной реакции: υ2 = k2[HI]2.
Если H2 и I2 – исходные вещества, то в первый момент скорость прямой реакции определяется их начальными концентрациями, а скорость обратной реакции равна нулю. По мере израсходования H2 и I2 и образования HI скорость прямой реакции уменьшается, а скорость обратной реакции возрастает. Спустя некоторое время обе скорости уравниваются, и в системе устанавливается химическое равновесие, т.е. число образующихся и расходуемых молекул HI в единицу времени становится одинаковым.
Так как, при химическом равновесии скорости прямой и обратной реакций равны V1 = V2, то k1 [H2] [I2]= k2 [HI]2.
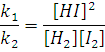
Поскольку k1 и k2 при данной температуре постоянны, то их отношение будет постоянным. Обозначая его через K, получим:
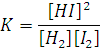
К – называется константой химического равновесия, а приведенное уравнение законом действующих масс (Гульдберга — Ваале).
В общем случае для реакции вида аА bB …↔dD eE … константа равновесия равна 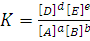 . Для взаимодействия между газообразными веществами часто пользуются выражением
. Для взаимодействия между газообразными веществами часто пользуются выражением 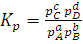 , в котором реагенты представлены равновесными парциальными давлениями p. Для упомянутой реакции
, в котором реагенты представлены равновесными парциальными давлениями p. Для упомянутой реакции 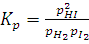 .
.
Состояние равновесия характеризует тот предел, до которого в данных условиях реакция протекает самопроизвольно (∆G<0). Если в системе наступило химическое равновесие, то дальнейшее изменение изобарного потенциала происходить не будет, т.е. ∆G=0.
Соотношение между равновесными концентрациями не зависит от того, какие вещества берутся в качестве исходных (например, H2 и I2 или HI), т.е. к состоянию равновесия можно подойти с обеих сторон.
Константа химического равновесия зависит от природы реагентов и от температуры; от давления (если оно слишком высокое) и от концентрации реагентов константа равновесия не зависит.
Влияние на константу равновесия температуры, энтальпийного и энтропийного факторов. Константа равновесия связана с изменением стандартного изобарно-изотермического потенциала химической реакции ∆Go простым уравнением ∆Go=-RT In K.
Из него видно, что большим отрицательным значениям ∆Go(∆Go<<0) отвечают большие значения К, т.е. в равновесной смеси преобладают продукты взаимодействия. Если же ∆Goхарактеризуется большими положительными значениями (∆Go>>0), то в равновесной смеси преобладают исходные вещества. Указанное уравнение позволяет по величине ∆Goвычислить К, а затем и равновесные концентрации (парциальные давления) реагентов. Если учесть, что ∆Go=∆Нo-Т∆So, то после некоторого преобразования получим 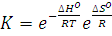 . Из этого уравнения видно, что константа равновесия очень чувствительна к изменению температуры. Влияние на константу равновесия природы реагентов определяет ее зависимость от энтальпийного и энтропийного факторов.
. Из этого уравнения видно, что константа равновесия очень чувствительна к изменению температуры. Влияние на константу равновесия природы реагентов определяет ее зависимость от энтальпийного и энтропийного факторов.
Принцип Ле Шателье
Состояние химического равновесия сохраняется при данных неизменных условиях любое время. При изменении же условий состояние равновесия нарушается, так как при этом скорости противоположных процессов изменяются в разной степени. Однако спустя некоторое время система снова приходит в состояние равновесия, но уже отвечавшее новым изменившимся условиям.
Смещение равновесия в зависимости от изменения условий в общем виде определяется принципом Ле-Шателье (или принципом подвижного равновесия): если на систему, находящуюся в равновесии, оказывать воздействие извне путем изменения какого-либо из условий, определяющих положение равновесия, то оно смещается в направлении того процесса, протекание которого ослабляет эффект произведенного воздействия.
Так, повышение температуры вызывает смещение равновесия в направлении того из процессов, течение которого сопровождается поглощением тепла, а понижение температуры действует в противоположном направлении. Подобно этому повышение давления смещает равновесие в направлении процесса, сопровождающегося уменьшением объема, а понижение давления действует в противоположную сторону. На пример, в равновесной системе 3Н2 N2 2H3N, ∆Ho= -46,2 кДж повышение температуры усиливает разложение H3N на водород и азот, так как этот процесс эндотермический. Повышение давления смещает равновесие в сторону образования H3N, ибо при этом уменьшается объем.
2H3N, ∆Ho= -46,2 кДж повышение температуры усиливает разложение H3N на водород и азот, так как этот процесс эндотермический. Повышение давления смещает равновесие в сторону образования H3N, ибо при этом уменьшается объем.
Если в систему, находящуюся в состоянии равновесия, добавить некоторое количество какого-либо из веществ, участвующих в реакции (или наоборот, удалить из системы), то скорости прямой и обратной реакций изменяются, но постепенно снова уравниваются. Иными словами, система снова приходит к состоянию химического равновесия. В этом новом состоянии равновесные концентрации всех веществ, присутствующих в системе, будут отличаться от первоначальных равновесных концентраций, но соотношение между ними останется прежним. Таким образом, в системе, находящейся в состоянии равновесия, нельзя изменить концентрацию одного из веществ, не вызвав изменения концентраций всех остальных.
В соответствии с принципом Ле Шателье введение в равновесную систему дополнительных количеств какого-либо реагента вызывает сдвиг равновесия в том направлении, при котором концентрация этого вещества уменьшается и соответственно увеличивается концентрация продуктов его взаимодействия.
Изучение химического равновесия имеет большое значение как для теоретических исследований, так и для решения практических задач. Определяя положение равновесия для различных температур и давлений, можно выбрать наиболее благоприятные условия проведения химического процесса. При окончательном выборе условий проведения процесса учитывают также их влияние на скорость процесса.
Пример 1. Вычисление константы равновесия реакции по равновесным концентрациям реагирующих веществ.
Вычислите константу равновесия реакции А В  2С, если равновесные концентрации [А]=0,3моль∙л-1; [В]=1,1моль∙л-1; [С]=2,1моль∙л-1.
2С, если равновесные концентрации [А]=0,3моль∙л-1; [В]=1,1моль∙л-1; [С]=2,1моль∙л-1.
Решение. Выражение константы равновесия для данной реакции имеет вид: 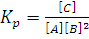 . Подставим сюда указанные в условии задачи равновесные концентрации:
. Подставим сюда указанные в условии задачи равновесные концентрации: 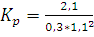 =5,79.
=5,79.
Пример 2. Вычисление равновесных концентраций реагирующих веществ. Реакция протекает по уравнению А 2В  С.
С.
Определите равновесные концентрации реагирующих веществ, если исходные концентрации веществ А и В соответственно равны 0,5 и 0,7 моль∙л-1, а константа равновесия реакции Кр=50.
Решение. На каждый моль веществ А и В образуется 2 моль вещества С. Если понижение концентрации веществ А и В обозначить через Х моль, то увеличение концентрации вещества будет равно 2Х моль. Равновесные концентрации реагирующих веществ будут:
СА=(о,5-х)моль∙л-1; СВ=(0,7-х)моль∙л-1; СС=2х моль∙л-1
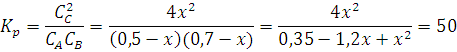
х1=0,86; х2=0,44
По условию задачи справедливо значение х2. Отсюда равновесные концентрации реагирующих веществ равны:
СА=0,5-0,44=0,06моль∙л-1; СВ=0,7-0,44=0,26моль∙л-1; СС=0,44∙2=0,88моль∙л-1.
Пример 3. Определение изменения энергии Гиббса ∆Go реакции по значению константы равновесия Кр. Рассчитайте энергию Гиббса и определите возможность протекания реакции СО Cl2=COCl2 при 700К, если константа равновесия равна Кр=1,0685∙10-4. Парциальное давление всех реагирующих веществ одинаково и равно 101325Па.
Решение. ∆G700=2,303∙RT 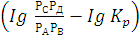 .
.
Для данного процесса: 
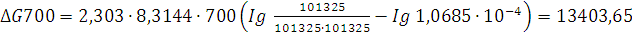
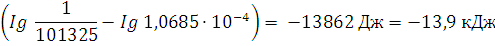
Так как ∆Gо<0, то реакция СО Cl2 COCl2 при 700К возможна.
COCl2 при 700К возможна.
Пример 4. Смещение химического равновесия. В каком направлении сместится равновесие в системе N2 3H2 2NH3-22ккал:
2NH3-22ккал:
а) при увеличении концентрации N2;
б) при увеличении концентрации Н2;
в) при повышении температуры;
г)при уменьшении давления?
Решение. Увеличение концентрации веществ, стоящих в левой части уравнения реакции, по правилу Ле-Шателье должно вызвать процесс, стремящийся ослабить оказанное воздействие, привести к уменьшению концентраций, т.е. равновесие сместится вправо (случаи а и б).
Реакция синтеза аммиака – экзотермическая. Повышение t вызывает смещение равновесия влево – в сторону эндотермической реакции, ослабляющей оказанное воздействие (случай в).
Уменьшение давления (случай г) будет благоприятствовать реакции, ведущей к увеличению объема системы, т.е. в сторону образования N2 и Н2.
Пример 5.Во сколько раз изменится скорость прямой и обратной реакции в системе 2SO2(г) О2(г)  2SO3(r) если объем газовой смеси уменьшится в три раза? В какую сторону сместится равновесие системы?
2SO3(r) если объем газовой смеси уменьшится в три раза? В какую сторону сместится равновесие системы?
Решение. Обозначим концентрации реагирующих веществ: [SO2] = а, [Q2] = b, [SO3] = с. Согласно закону действующих масс, скорости прямой и обратной реакций до изменения объема равны
vпр= Ка2b, vобр = К1с2
После уменьшения объема гомогенной системы в три раза концентрация каждого из реагирующих веществ увеличится в три раза: [SO2] = 3а, [О2] = 3b; [SO3] = 3с. При новых концентрациях скорости v’np прямой и обратной реакций:
v’np = K(3a)2 (3b) = 27 Ka2b; vo6p = K1(3c)2 = 9K1c2 .
Отсюда
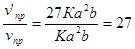 ;
; 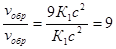
Следовательно, скорость прямой реакции увеличилась в 27 раз, а обратной — только в девять раз. Равновесие системы сместилось в сторону образования SO3.
Пример 6.Вычислите, во сколько раз увеличится скорость реакции, протекающей в газовой фазе, при повышении температуры от 30 до 70 0С, если температурный коэффициент реакции равен 2.
Решение. Зависимость скорости химической реакции от температуры определяется эмпирическим правилом Вант-Гоффа по формуле
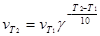 ;
; 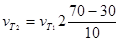 =
= 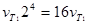
Следовательно, скорость реакции vT  при 70°С большескорости реакции vT
при 70°С большескорости реакции vT  при 30° С в 16 раз.
при 30° С в 16 раз.
Пример 7.Константа равновесия гомогенной системы
СО(г) Н2О(г)  СО2(г) Н2(г) при 850°С равна 1. Вычислите концентрации всех веществ
СО2(г) Н2(г) при 850°С равна 1. Вычислите концентрации всех веществ  при равновесии, если исходные концентрации: [СО]ИСХ = 3 моль/л, [Н2О]ИСХ = 2 моль/л.
при равновесии, если исходные концентрации: [СО]ИСХ = 3 моль/л, [Н2О]ИСХ = 2 моль/л.
Решение. При равновесии скорости прямой и обратной реакций равны, а отношение констант этих скоростей постоянно и называется константой равновесия данной системы:
Vnp – К 1[СО][Н2О]; vo6p = К2[СО2][Н2];
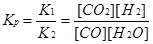
В условии задачи даны исходные концентрации, тогда как в выражение Крвходят только равновесные концентрации всех веществ системы. Предположим, что к моменту равновесия концентрация [СО2]Р = х моль/л. Согласно уравнению системы число молей образовавшегося водорода при этом будет также х моль/л. По столько же молей (х моль/л) СО и Н2О расходуется для образования по х молей СО2 и Н2 . Следовательно, равновесные концентрации всех четырех веществ (моль/л):
[СО2]Р = [Н2]р = х; [СО]Р = (3 –х); [H2O]P =(2-х).
Зная константу равновесия, находим значение х, а затем исходные концентрации всех веществ:
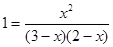 ; х2=6-2х-3х х2; 5х = 6, л = 1,2 моль/л.
; х2=6-2х-3х х2; 5х = 6, л = 1,2 моль/л.
Таким образом, искомые равновесные концентрации: [СО2]Р = 1,2 моль/л; [Н2]р = 1,2 моль/л; [СО]Р= 3 — 1,2 = 1,8 моль/л; [Н2О]Р = = 2- 1,2 = 0,8 моль/л.
Пример 8.Эндотермическая реакция разложения пента-хлорида фосфора протекает по уравнению
РС15(г)  РС13(г) С12(г); ∆Н = 92,59 кДж.
РС13(г) С12(г); ∆Н = 92,59 кДж.
Как надо изменить: а) температуру; б) давление; в) концентрацию, чтобы сместить равновесие в сторону прямой реакции — разложения РСl5?
Решение. Смещением или сдвигом химического равновесия называют изменение равновесных концентраций реагирующих веществ в результате изменения одного из условий реакции. Направление, в котором сместилось равновесие, определяется по принципу Ле Шателье: а) так как реакция разложения РС15 эндотермическая (∆Н > 0), то для смещения равновесия в сторону прямой реакции нужно повысить температуру: б) так как в данной системе разложение РС15 ведет к увеличению объема (из одной молекулы газа образуются две газообразные молекулы), то для смещения равновесия в сторону прямой реакции надо уменьшить давление; в) смещения равновесия в указанном направлении можно достигнуть как увеличением концентрации РС15, так иуменьшением концентрации РСl3 или С12
ДИСПЕРСНЫЕ СИСТЕМЫ
Дисперсная система – это система из двух (или более) веществ, одно из которых (называемое дисперсной фазой) равномерно распределено в другом (называемом дисперсионной средой).
Различают несколько видов дисперсных систем в зависимости от степени дисперсности, т.е. величины, обратной среднему радиусу частиц дисперсной фазы: D=I/r. Радиус частиц выражается в нанометрах (нм). Наиболее грубыми дисперсными системами являются взвеси с размером частиц более 100 нм. Они представляют собой гетерогенные нестабильные во времени системы, в которых, однако, взвешенные частицы сохраняют все свойства фазы.
Микрогетерогенные системы с размером частиц 1…100нм представляют собой коллоидные растворы, занимающие промежуточное положение между взвесями и истинными растворами, т.е. гомогенными системами с размером частиц менее 1нм, неограниченно стабильными во времени. Истинные растворы определяют еще как многокомпонентные однофазные системы переменного состава, находящиеся в состоянии химического равновесия.
§
Для количественной характеристики растворов используют понятие концентрации:
Концентрация – величина, выражающая относительное содержание данного компонента в системе (смеси, растворе).
Из концентраций растворов, наибольшее применение в химии находят следующие:
Процентная концентрация растворов показывает число единиц массы растворенного вещества, содержащееся в 100 единицах массы раствора и для его приготовления следует взять 12 единиц массы СаСl2 и 88 единиц массы растворителя.
Молярная концентрация раствора (молярность) – отношение количества этого вещества, содержащегося в растворе (в молях), к объему раствора: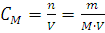 , где m – масса растворенного вещества, г; М – молярная масса растворенного вещества, г∙моль-1; V – объем раствора, л. Единица Си – моль∙м-3, обычно применяют моль∙л-1.
, где m – масса растворенного вещества, г; М – молярная масса растворенного вещества, г∙моль-1; V – объем раствора, л. Единица Си – моль∙м-3, обычно применяют моль∙л-1.
Молярным называется раствор, в 1л которого содержится 1 моль растворенного вещества.
Эквивалентная (нормальная) концентрация раствора (нормальность) – отношение числа эквивалентов вещества, содержащегося в растворе, к объему раствора: 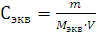 , где m – масса растворенного вещества; Мэкв – молярная масса эквивалента растворенного вещества.
, где m – масса растворенного вещества; Мэкв – молярная масса эквивалента растворенного вещества.
Единица эквивалентной концентрации в СИ – моль∙м-3, обычно применяют моль∙л-1.
Молярная концентрация раствора (моляльность) определяется числом молей растворенного вещества в 1кг (1000г) растворителя. Единица моляльности раствора в СИ – моль∙кг-1, можно применять моль∙г-1.
Основная особенность моляльного способа выражения концентрации заключается в том, что моляльная концентрация раствора не зависит от температуры, поскольку для определения моляльности не привлекается объем.
Массовой долей растворенного вещества называют отношение массы растворенного вещества к общей массе раствора. Массовую долю обычно выражают в долях единицы и обозначают W.
Мольная доля – отношение числа молей данного вещества в растворе к общему числу молей веществ, образующих раствор.
Для приготовления растворов заданных концентраций должны проводиться соответствующие расчеты.
Пример 1. Какой массы кристаллогидрат ВаCl2∙2H2O надо взять для приготовления раствора объемом 0,5л, в котором массовая доля ВаСl2 составляет 0,1 (10%-ный раствор)?
Решение. Если W(BaCl2) =0,1 или 10%, то плотность раствора р=1,090г∙см-3 (из справочных таблиц). Тогда масса раствора BaCl2 заданного объема равна 500∙1,090=545,0 (г). Масса BaCl2 в этом растворе находится из пропорции:
m(BaCl2) – m(р-ра BaCl2)
10 г – 100 г
х г – 545 г
х = 54,5г
Масса кристаллогидрата:
m(BaCl2*2H2O) – m(BaCl2)
244,2г – 208,4г
х г – 54,5г
х = 64,0 г
Пример 2. Какова масса KCl, содержащегося в 0,5л раствора, если молярная концентрация раствора 0,2 моль∙л-1?
Решение. Молярную концентрацию(моль∙л-1) выражают формулой: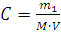 , где m1 – масса растворенного вещества, г; M – молярная масса растворенного вещества, г∙моль-1; V – объем раствора, л.
, где m1 – масса растворенного вещества, г; M – молярная масса растворенного вещества, г∙моль-1; V – объем раствора, л.
M(KCl) = 74,5г∙моль-1. Масса KCl, содержащегося в растворе, равна m1=M*V*C=0,2∙0,5∙74,5=7,45г.
Пример 3. Определите эквивалентную концентрацию хлорида железа(3), если в 0,3л раствора содержится 32,44г PeCl3.
Решение. Эквивалентная концентрация (нормальность раствора) рассчитывается по формуле:
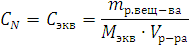
Молярная масса эквивалента PeCl3 равна:
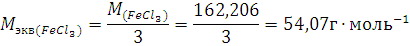
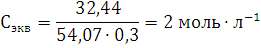
Пример 4. В какой массе воды надо растворить 5,85г хлорида натрия, чтобы получить раствор, моляльность которого равна 0,3моль∙г-1.
Решение. Моляльность раствора рассчитывается по формуле:
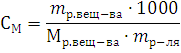
где mр-ля – масса растворителя в г. Отсюда:
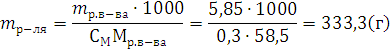
Пример 5.Вычисления, связанные с пересчетом концентраций растворов из одних единиц в другие.
Вычислите эквивалентную концентрацию, молярную концентрацию и моляльность раствора, в котором массовая доля СиSO4 равна 0,10. Плотность раствора 1107кг∙м-3.
Решение. Определим молярную массу и молярную массу эквивалента СиSO4.
M(СиSO4) = 160г∙моль-1; Мэкв(СиSO4) = 160/2=80г∙моль-1.
В 100 г раствора с ω(СиSO4)=0,1 содержится 10,0г СиSO4 и 90 г H2O. Следовательно, СМ раствора СиSO4 равна:
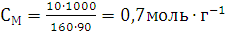 .
.
СМ и Сэкв относятся к 1 литра раствора: m=p∙V=1107∙10-3=1,107кг. В этой массе раствора содержится 1,107∙0,1=0,1107кг СиSO4, что составляет 110,7/159,61=0,693 моль или 0,693∙2=1,386экв.
Молярная концентрация и эквивалентная концентрация данного раствора соответственно равны 0,693 и 1,386моль∙л-1.
Пример 6. Расчеты, связанные с приготовлением разбавленных растворов из концентрированных.
Какой объем раствора азотной кислоты массовой долей HNO3 0,3(p=1180кг∙м-3) требуется для приготовления 20л 0,5 М раствора этой кислоты?
Решение. Сначала определяем массу азотной кислоты в 20л 0,5 М раствора:
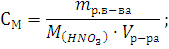
М(HNO3) = 63г∙моль-1; mр.в-ва = 0,5∙63∙20=630г.

Так как
; Следовательно для приготовления 20л 0,5 М раствора HNO3, надо израсходовать всего 1,78л раствора азотной кислоты 30%-й концентрации.
Пример 7. Вычислите :а) массовую(процентную) (с,%); б) молярную концентрацию (см); молярную концентрацию эквивалента (сн); г) молярную (см) концентрацию раствора Н3РО4, полученного при растворении 18 г кислоты в 282 см3 воды, если плотность его 1,031г/см3. Чему равен титр Т этого раствора?
Решение: а) Массовая концентрация показывает число граммов (единиц массы) вещества, содержащееся в 100 г (единиц массы) раствора. Так как массу 282 см3 воды модно принять равной 282 г, то масса полученного раствора 18 282 = 300 г и, следовательно:
300-18
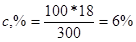
100-с,%
б) молярная (мольно-объемная)% концентрация показывает число молей растворенного вещества, содержащихся в 1 л раствора. Масса 1 л раствора 1031 г. Массу кислоты в литре раствора находим из соотношения
300-18
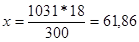
1031-х
Молярную концентрацию раствора получим делением числа граммов Н3РО4 в 1 л раствора на молярную массу Н3РО4 (97,99 г/моль):
см = 61,86/97,99 = 0,63 М.
в) молярная концентрация эквивалента (или нормальность)
показывает число эквивалентов растворенного вещества,
содержащихся в 1 л раствора.
Так как эквивалентная масса Н3РО4 = М/ 3 = 97,99/3 = 32,66 г/моль, то
с н = 61,86/32,66= 1,89 н.;
г) моляльная концентрация (или моляльность) показывает
число молей растворенного вещества, содержащихся в 1000 г
растворителя. Массу Н3РО4 в 1000 г растворителя находим из
соотношения
282-18
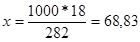
1000-х
Отсюда см = 63,83/97,99 = 0,65 м.
Титром раствора называют число граммов растворенного вещества в 1 см3 (мл) раствора. Так как в 1 л раствора содержится 61,8б г кислоты, то Т= 61,86/1000 = 0,06186 г/см3
Зная молярную концентрацию эквивалента и молярную массу эквивалента (тэ) растворенного вещества, титр легко найти по формуле
Т=снmэ/1000.
Пример 8.На нейтрализацию 50 см3 раствора кислоты израсходовано 25 см3‘ 0,5 н. раствора щелочи. Чему равна молярная концентрация эквивалентов кислоты?
Решение. Так как вещества взаимодействуют между собой в эквивалентных соотношениях, то растворы равной молярной концентрации эквивалентов реагируют в равных объемах. При разных молярных концентрациях эквивалентов объемы растворов реагирующих веществ обратно пропорциональны их норма-льностям, т.е.
V1:V2 =CH2 : СН1или V1∙СН1=V2∙CH2
50 СН1 = 25 ∙ 0,5 откуда CH1= 25 ∙0,5 / 50 = 0,25н
Пример 9.К 1 л 10%-ного раствора КОН (пл. 1,092 г/см3) прибавили 0,5 л 5%-ного раствора КОН (пл. 1,045 г/см3). Объем смеси довели до 2 л. Вычислите молярную концентрацию полученного раствора.
Решение. Масса одного литра 10%-ного раствора КОН равна 1092 г. В этом растворе содержится 1092 ∙10/100 = 109,2 г КОН. Масса 0,5 л 5%-ного раствора 1045 ∙ 0,5 = 522,5 г. В этом растворе содержится 522,5 ∙ 5/100 = 26,125 г КОН.
В общем объеме полученного раствора (2 л) содержание КОН составляет 109,2 26,125 = 135,325 г. Отсюда молярная концентрация раствора см = 135,325/(2 ∙ 56,1) = 1,2 М, где 56,1 г/моль — молярная масса КОН.
Пример 10.Какой объем 96%-ной кислоты плотностью 1,84 г/см3 потребуется для приготовления 3 л 0,4 н. раствора?
Решение. Эквивалентная масса H2SO4 = М/2 = 98,08/2 = 49,04 г/моль. Для приготовления 3 л 0,4 н. раствора требуется 49,04∙0,4∙3= = 58,848 г H2SO4. Масса 1 см3 96%-ной кислоты 1,84 г. В этом растворе содержится 1,84 ∙ 96/100 = 1,766 г H2SO4.
Следовательно, для приготовления 3 л 0,4 н. раствора надо взять 58,848 : 1,766 = 33,32 см3 этой кислоты.
§
Осмотическое давление прямо пропорционально молярной концентрации раствора (СМ) и абсолютной температуре (Т). Эта зависимость дается уравнением Вант-Гоффа: Росм=СМRT, где R – универсальная газовая постоянная, значение которой определяется принятыми единицами измерения. Если давление измерять в Па, а объем в м3, то R=8,3144∙103Дж∙моль-1∙К-1; Т – абсолютная температура.
Поскольку СМ=n/V, то уравнение Вант-Гоффа аналогично уравнению Менделеева-Клапейрона, которое характеризует газовое состояние вещества:
РосмV=nRT или 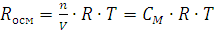 ,
,
где n – число молей растворенного вещества; V – объем раствора. Заменяя СМ в выражении Р=СМRT его выражением по формуле для молярной концентрации 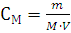 , где m – масса растворенного вещества; М – молярная масса растворенного вещества, получим формулу, удобную для вычисления молярной массы растворенного вещества [2].
, где m – масса растворенного вещества; М – молярная масса растворенного вещества, получим формулу, удобную для вычисления молярной массы растворенного вещества [2].
Пример 1. Вычисление осмотического давления растворов. Определить величину осмотического давления раствора, если в 500мл раствора содержится 1,8г глюкозы С4Н12О6 при 25оС.
Решение. Осмотическое давление раствора определяют согласно закону Вант-Гоффа: 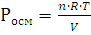 . В 0,5л раствора содержится 1,8 глюкозы, молярная масса которой равна 180г∙моль-1. Следовательно, в 0,5л раствора содержится n=1,8*180=0,01моль глюкозы.
. В 0,5л раствора содержится 1,8 глюкозы, молярная масса которой равна 180г∙моль-1. Следовательно, в 0,5л раствора содержится n=1,8*180=0,01моль глюкозы.
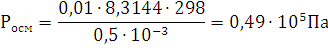
Пример 2. Вычисление молярной массы неэлектролита по относительному понижению давления пара растворителя над раствором.
Навеска вещества массой 12,42г растворена в воде объемом 500мл. Давление пара полученного раствора при 20оС равно 3732,7Па. Давления пара воды при той же температуре 3742Па. Как по этим данным найти молярную массу (М) растворенного вещества?
Решение. Для определения М надо вычислить n, пользуясь законом Рауля: 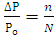 , откуда
, откуда 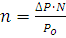 , так как ∆Р=3742-3732,7=9,3Па и
, так как ∆Р=3742-3732,7=9,3Па и 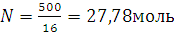 , то
, то 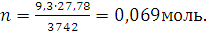
Поскольку 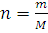 , то
, то 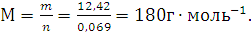
§
Давление пара растворов ниже давления пара чистых растворителей при той же температуре. Понижение давления пара ∆Р, отнесенное к Ро(∆Р/Ро) называют относительным понижением давления насыщенного пара раствора.
Закон Рауля: относительное понижение давления насыщенного пара растворителя над раствором равно молярной доле растворенного вещества, т.е. 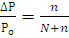 , где N и n – количества растворителя и растворенного вещества соответственно. Закон Рауля используют для определения молярной массы вещества.
, где N и n – количества растворителя и растворенного вещества соответственно. Закон Рауля используют для определения молярной массы вещества.
Пример 1. Вычисление давления пара растворителя над раствором. Определите давление пара растворителя над раствором, содержащим 1,212*1023 молекул неэлектролита в 100г воды при 100оС. Давление пара воды при 100оС равно 1,0133*105Па.
Решение. Относительное понижение давления пара растворителя над раствором согласно закону Рауля выражается соотношением: 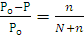 . Количество растворителя N и растворенного вещества n находим:
. Количество растворителя N и растворенного вещества n находим:
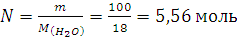 ;
; 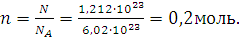
Давление пара над раствором:
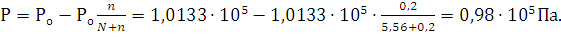
Пример 2. Вычисление молярной массы неэлектролита по относительному понижению давления пара растворителя над раствором.
Рассчитайте молярную массу неэлектролита, если 28,5г этого вещества, растворенного в 745г воды, вызывают понижение давления пара воды над раствором на 52,37 Па при 40оС. Давление водяного пара при этой же температуре равно 7375,9 Па.
Решение. Относительное понижение давления пара растворителя над раствором равно: 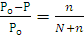 . Находим:
. Находим: 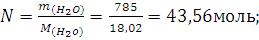
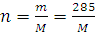 , где m – масса неэлектролита, молярная масса которого М г∙моль-1.
, где m – масса неэлектролита, молярная масса которого М г∙моль-1. 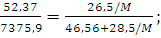 0,309 М 0,202 = 28,5. 0,309 М = 28,298; М=91,58г∙моль-1.
0,309 М 0,202 = 28,5. 0,309 М = 28,298; М=91,58г∙моль-1.
Молярная масса неэлектролита равна ≈92г*моль-1.
§
Растворы замерзают при более низкой температуре, а кипят при более высокой температуре, чем чистый растворитель. Понижение температуры замерзания и повышение температуры кипения раствора пропорционально моляльно концентрации растворенного вещества(Второй закон Рауля), т.е. ∆toзам=КК∙С; ∆toкип=КЭ∙С; где ∆toзам – понижение температуры замерзания раствора; ∆toкип – повышение температуры кипения раствора; КК – криоскопическая константа; КЭ – эбуллиоскопическая константа; С – моляльная концентрация растворенного вещества.
Если «m» граммов неэлектролита, имеющего молярную массу М, растворены в m граммах растворителя, то закон Рауля для неэлектролитов можно записать в следующем виде: 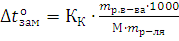 и
и 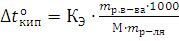
Указанные формулы позволяют находить молярную массу растворенного вещества.
Пример 1. Определение температуры кипения и замерзания раствора неэлектролита.
Определите температуру кипения и замерзания раствора, содержащего 1г нитробензола С6Н5NO2 в 10г бензола. Эбулилиоскопическая и криоскопическая константы бензола соответственно равны 2,57 и 51оС.
Решение. По закону Рауля следует, что
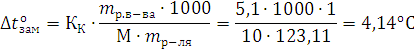
Тогда 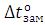 равна
равна 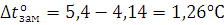
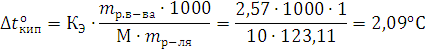
Температура кипения раствора: 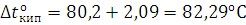 .
.
Пример 2.Вычисление молярной массы неэлектролита по повышению температуры кипения раствора.
Раствор камфоры массой 0,552г в 17г эфира кипит при температуре на 0,461оС выше, чем чистый эфир. Эбулиоскопическая константа эфира 2,16оС. Определите молярную массу камфоры.
Решение. Молярную массу камфоры определяем пользуясь соотношением:
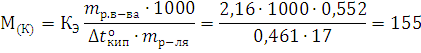
Молярная масса камфоры равна 155,14г∙моль-1.
Пример 3. Вычисление криоскопической константы растворителя. Вычислите криоскопическую константу воды, если водный раствор этилового спирта (ω=0,113) замерзает при -5оС.
Решение. Молярная масса этилового спирта равна 46,07. Из соотношения, проведенного в примере 1, получаем:
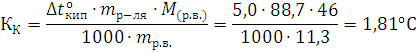
Криоскопическая константа воды КК = 1,81оС.
Пример 4. Вычислите температуры кристаллизации и кипения 2% -ного водного раствора глюкозы.
Решение. По закону Рауля понижение температуры кристаллизации и повышение температуры кипения раствора (∆Т) по сравнению с температурами кристаллизации и кипения растворителя выражаются уравнением
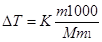 (1)
(1)
где К — криоскопическая или эбулиоскопическая константа. Для воды они соответственно равны 1,86 и 0,52°; т и М — соответственно масса растворенного вещества и его молярная масса; т1— масса растворителя.
Понижение температуры кристаллизации 2%-ного раствора С6Н12О6 находим по формуле (1):
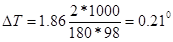
Вода кристаллизуется при 0 С, следовательно, температура кристаллизации раствора 0 — 0,21 = — 0,21 С.
По формуле (1) находим и повышение температуры кипения-2%-ного раствора:
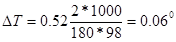
Вода кипит при 100°С, следовательно, температура кипения этого раствора 100 0,06 = 100,06°С.
Пример 5.Раствор, содержащий 1,22 г бензойной кислоты С6Н5СООН в 100 г сероуглерода, кипит при 46,529°С. Температура кипения сероуглерода 46,3°С. Вычислите эбулиоскопическую константу сероуглерода.
Решение. Повышение температуры кипения ДТ = 46,529 — 46,3 = = 0,229°. Молярная масса бензойной кислоты 122 г/моль. По формуле (1) находим эбулиоскопическую константу:
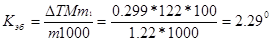
Пример 6.Раствор, содержащий 11,04 г глицерина в 800 г воды, кристаллизуется при -0,279°С. Вычислите молярную массу глицерина.
Решение. Температура кристаллизации чистой воды 0 0С, следовательно, понижение температуры кристаллизации ∆Т=
=0 — (-0,279) = 0,2790С . Масса глицерина т (г), приходящаяся на 1000 г воды, равна:
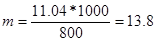
Подставляя в уравнение
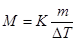 (2)
(2)
числовые значения, вычисляем молярную массу глицерина:
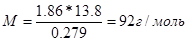
Пример 7. Вычислите массовую долю(%) водного раствора мочевины (NH2)2CO, зная, что температура кристаллизации этого раствора равна -0,4650С.
Решение: Температура кристаллизации чистой воды 00С, следовательно ∆Т = 0 – (-0,465) = 0,4650. Молярная масса мочевины 60 г/моль. Находим массу m (г) растворенного вещества, приходящуюся на 1000г воды, по формуле(2):
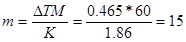
Общая масса раствора, содержащего 15г мочевины, составляет 1000 15=1015г. Процентное содержание мочевины в данном растворе находим из соотношения
В 1015г раствора – 15г вещества
В 100 г раствора – х
х = 1,48%
§
(при См= 1 моль/литр, =25 ºС)
| Электролит | α, % | Электролит | α, % | Электролит | α, % |
| HNOз | 82,0 | Н3РО4 | 29,0 | НСN | 0,01 |
| HCl | 78,4 | Н2SеО4 | 20,0 | NН4ОН | 1,4 |
| H2SO2 | 58,0 | HF | 8,0 | Н2S | 0,07 |
| КОН | 77,0 | CH2COOH | 1,36 | ||
| NaОН | 73,0 | Н2СО3 | 0,17 |
Концентрация ионов в растворе электролита зависит от молярной концентрации См, степени диссоциации α и числа ионов данного вида ni, на которое распадается молекула электролита.
Сионов=См∙αni. Например, для раствора Н2SO4 0,5 моль/л при α=50% концентрация ионов водорода [Н ]=0,5∙0,5∙2 моль/л.
Все соли, за исключением HgCl2 и Fe(CHS)3 – сильные электролиты.
Сильные и слабые электролиты имеют свои особенности.
При растворении слабых электролитов в воде происходит обратимая диссоциация, например, для СН3СООН имеет место равновесие:
СН3СООН  Н СН3СОО‾, т.е. процесс обратим.
Н СН3СОО‾, т.е. процесс обратим.
Для обратимого равновесного процесса можно применить закон действующих масс. Константа равновесия в данном случае называется константой диссоциации:
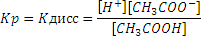
Константа диссоциации характеризует способность слабого электролита к распаду на ионы. Чем меньше величина Кдисс, тем слабее электролит. Например,
КСН3СООН = 1,82∙10-5, КНСN= 7,2∙10‾ ¹º , КНСN<КСН3СООН, т.е. НСN – более слабая кислота.
Обратимая диссоциация происходит в растворе слабого основания, например
NН4ОН  NН4 ОН‾;
NН4 ОН‾;
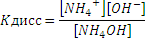
Кдисс = 1,76∙10-5, т.е. NН4ОН – слабое
Если электролит диссоциирует по ступеням, то каждая ступень характеризуется своей константой диссоциации:
Н3РО4 Н Н2РО4 КI=7,6∙10-3
Н Н2РО4 КI=7,6∙10-3
Н2РО4 Н НРО4 К2=6,2∙10-8
Н НРО4 К2=6,2∙10-8
НРО4 Н РО4‾ К3=4,4∙10-13 КI>К2>К3.
Н РО4‾ К3=4,4∙10-13 КI>К2>К3.
Диссоциация в основном идёт по первой ступени, по третьей ступени на электролит практически не диссоциирует, о чём свидетельствует малая величина К3.
Удобнее пользоваться не величинами Кдисс, а величинами рК-показателями кислоты и основания:
pКкислоты = -lgКкислоты, рКоснования =-lgКоснования.
Для Н3Р04: рК1=2,12; рК2= 7,21; рК3= 12,26.
Для характеристики свойств амфотерных электролитов необходимо знать величины констант диссоциации по кислотному и основному типам. По соотношению величин этих констант можно судить о преобладании тех или иных свойств у амфотерного электролита.
Напомним, что диссоциация амфотерного электролита проходит по
следующему уравнению (запись в общем виде):
R ОНֿ  ROH
ROH  H ROֿ. Тогда для Ве(0Н)2, например равновесие диссоциации имеет вид: Ве² 2OHֿ
H ROֿ. Тогда для Ве(0Н)2, например равновесие диссоциации имеет вид: Ве² 2OHֿ  Ве(OН)2
Ве(OН)2 H2BeO2
H2BeO2  2H Be22-;константа диссоциации по основному типу:
2H Be22-;константа диссоциации по основному типу:
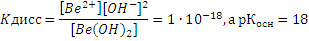
по кислотному типу
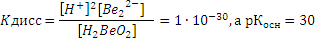
Поскольку Коск>Ккисл, у Ве(ОН)2 преобладают основные свойства.
В случае А1(0Н)3 Косн = 8 ∙10-25, Ккисл = 4∙10-13, следовательно, у А1(OН)3 преобладают кислотные свойства.
Примером электролита, у которого основные и кислотные свойства выражены примерно одинаково, может служить Ga(OH)3, у которого Ккисл=2∙10-12
Константа диссоциации зависит от природы вещества и температуры , но не зависит от концентрации, поэтому она дает более общую
характеристику электролита, чем α .
§
Примером гетерогенной системы может служить насыщенный раствор
труднорастворимого соединения, находящегося в равновесие с твердой фазой. К труднорастворимым веществам относятся многие электролиты — соли, основания (чаще всего амфотерные), некоторые кислоты
(H2SiO3; β-H2SnO3 и др.). Так, трудно растворимы галогениды
серебра, сульфаты бария и стронция, карбонаты бария и кальция. Сульфиды металлов за исключением сульфидов натрия и аммония
характеризуются очень малой растворимостью. Вследствие малой растворимости раствор труднорастворимого электролита становится насыщенным при очень малых концентрациях растворенного вещества.
Между твердой фазой и раствором электролита устанавливается равновесие, например, AgCl  Ag CI—
Ag CI—
твердая насыщенный
фаза раствор
В единицу времени в насыщенный раствор переходит сколько ионов, сколько их вновь переходит в осадок. Это состояние равновесия характеризуется величиной константы равновесия
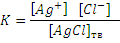
Концентрация твердой фазы – величина постоянная, т.е. [AgCl]тв= const, следовательно [Ag ][Cl—] также величина постоянная, называемая произведением растворимости (ПР): ПРAgCI=[Ag ]∙[CI—].
Таким образом, в насыщенном растворе труднорастворимого соединения произведение концентраций его ионов при данной температуре
есть величина постоянная. При написании ПР необходимо учитывать
стехиометрические коэффициенты в уравнении диссоциации соединения, например: ПРAg2CrO4=[Ag ]2[CrO42-]; ПРAg3PO4=[Ag ]3[PO43-];: ПРAg2S3=[Ag ]2[S2-]3.
В общем виде для системы КmAn↔mkn nAn, ПР выразится следующим образом: ПРKmAn=[Kn ]m[Am—]n.
Из понятия ПР вытекает условие образования и растворения осадков. Если =[Kn ]m[Am—]n= ПРKmAn , система находится в равновесии.
Если=[Kn ]m [Am—]n>ПРKmAn или =[Kn ]m [Am—]n<ПРKmAn, система стремится к новому состоянии равновесия, приводящему в первом случав к выпадению осадка, во втором — к его растворению. Эти процессы будут происходить до
тех пор, пока не будут достигнуты ионные концентрации, соответствующие величине произведения растворимости. В таблице 4 приведены
примеры некоторых труднорастворимых веществ.
Таблица 4
Произведение растворимости некоторых труднорастворимых веществ
| Вещество | ПР | Вещество | ПР |
| CuS | 6,3∙10-36 | α- ZnS | 1,6∙10-24 |
| Cu2S | 25∙10-48 | β — ZnS | 2,5∙10-22 |
| HgS | 3∙10-52 | ZnSe | 1∙10-21 |
Физико-химические свойства растворов электролитов.
Примеры решения задач.
Пример 1. Вычисление кажущейся степени диссоциации сильного электролита.
Вычислить степень диссоциации 0,2 М раствора муравьинной кислоты HCOOH, если Кд=2,1∙10-4.
Решение: По закону разбавления α=√(Кд/См) = √(2,1∙10-4/0,2)=3,24∙10-2 или 3,24%.
Пример 2. Вычисление степени диссоциации электролита по осмотическому давлению его раствора.
Рассчитайте кажущуюся степень электролитической диссоциации ZiCIв 0,1 М раствора соли, если раствор изотоничен с 0,19 М раствором сахара С12Н22О11 при 0ºС.
Решение: Моль сахара равен 342 г.
Росм=(mRT)/(M∙V)= (342∙0,19∙8,3144∙273)/ (342∙10-3) = 4,31∙105 Па.
М(ZiCI)=42 г∙моль-1. По осмотическому давлению определяем изотонический коэффициент раствора ZiCI
i=(Pосм∙V)/(nRT)=(4,31∙103∙10-3∙42,39)/(4,239∙8,3144∙273)= 1,19.
Кажущаяся степень диссоциации в 0,1 М ZiCI равна α=(i-1)/(n-1)=(1,9-1)/(2-1)=0,9 или 90 %.
Пример 3. Вычисление степени диссоциации электролита по понижению давление пара растворителя над раствором.
Давление пара водного раствора NaNO3(ω=0 ,08) равно 2268,8 Па при 20 °С. Давление паров воды при этой температуре равно 2337,8 Па. Найдите кажущуюся степень диссоциации нитрата натрия в этом растворе.
Решение. С помощью первого закона Рауля для электролитов вычисляем значение изотонического коэффициента для NaNO3
ι = (P0-P) ∙ (N n)/P0∙n ;M(NaNO3) = 85,00 г∙моль-1; n=8:85=0,094 моль; М (Н2О)=18,02 г∙моль-1;
ι = (2337,8-2268,9) ∙ (0,094 5,911)/(2337,8∙0,094)=(0,69∙5,199)/219,75 = 1,63.
Кажущаяся степень диссоциации NaNO3 в этом растворе равна
α=(1,63-1)/(2-1) = 0,63 (или 63 %).
Пример 4. Вычисление изотонического коэффициента по повышению температуры кипения раствора.
Раствор, содержащий 8 г NaOH в 1000 г Н2О, кипит при 100,184°С.
Определите изотонический коэффициент (для воды Е =-0,516°С).
Решение. Второй закон Рауля для растворов электролитов выражается уравнением ∆t0кип=ι∙ (Кэ∙100∙m)/(mр-ля∙М(р.в)). Тогда
ι = (∆t0кип∙mр-ля*М(р.в))/(Кэ∙m∙1000)= (0,184∙1000∙40)/(0,516∙1000∙8)=1,78.
§
Электростатическое взаимодействие полярных молекул воды приводит к их самоионизации: 2Н2О↔Н3О ОН— или в упрощенной форме Н2О↔Н ОН—;
Константа диссоциации воды весьма мала при 25°С/
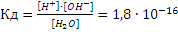
Принимая поэтому концентрацию воды [Н2О] величиной практически постоянной, можно записать К∙ [Н2О]=[Н ] ∙ [ОН—] = 1,8∙10-16[Н2О]. Но концентрация воды равна 1000/18=55,56 моль∙л-1, отсюда получаем [Н ]∙[ОН—] = =1,8∙10-16∙55,56=1∙10-14=Кв.
Произведение концентраций ионов водорода и ионов гидроксида называется ионным произведением воды Кв. Ионное произведение воды
есть величина постоянная при постоянной температуре. В чистой воде и нейтральных растворах[Н ]=[ОН—]=√10-14=10-7 моль∙л-1.
Математически более удобной характеристикой среды является водородный показатель рН, равный десятичному логарифму концентрации водородных ионов, взятому с обратным знаком: рН = -lg[Н ].
Тогда рН различных растворов будут иметь следующие значения:
кислый рН <7;
нейтральный рН = 7;
щелочной рН >7.
Аналогично, отрицательный десятичный логарифм концентрации гидроксо-ионов называется гидроксильным показателем и обозначается рОН. Следовательно,
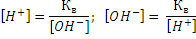
рН рОН = 14.
Пример 1. Вычисление водородного показателя раствора.
Вычислите водородный показатель рН раствора гидроксида натрия, содержащегося в растворе в концентрации 4,2∙10-3 моль∙л-1 .
Решение. Концентрация ОН— ионов в растворе NaOH равна [0Н—] =4,2∙10-3 моль ∙ л -1. Исходя из ионного произведения воды Кв, находим концентрацию ионов водорода: [Н ] = КВ/[ОН—]=10-14/4,2∙10-3=0,24∙10-11. Водородный показатель раствора NaOH равен: рН= -lg([Н ])=-lg(0,24∙10-11)=11,62.
Пример 2.Определение концентрации ионов Н и ОН— в растворах сильных кислот и оснований.
Определите концентрацию ионов водорода и рН в 0,01 М раствора соляной кислоты.
Решение. Соляная кислота — сильный электролит, в растворе полностью диссоциирует на ионы: НС1  Н С1—. Концентрация ионов [Н ] численно равна концентрации НС1. Из 0,01 моль НС1 образуется 0,01 моль иона Н . Отсюда, [Н ] =0,01∙10-2; рН=-lg(1∙10-2)=2.
Н С1—. Концентрация ионов [Н ] численно равна концентрации НС1. Из 0,01 моль НС1 образуется 0,01 моль иона Н . Отсюда, [Н ] =0,01∙10-2; рН=-lg(1∙10-2)=2.
Пример 3. Вычисление рН сильного электролита с учетом его коэффициента активности.
Найдите водородный показатель раствора НNO3, если его молярная концентрация равна 0,178 моль∙л-1.
Решение. При значительной концентрации сильного электролита его активная концентрация существенно отличается от истинной. Поэтому в таких случаях нужно вводить поправку на активность электролита. Определяем ионную силу раствора НNO3: J= 1/2∙ (0,176∙I2 0,178∙I2) = 0,356/2 = 0,178.
Далее по вычисленной ионной силе находим коэффициент активности иона [Н ]= f(Н )=0.838. Тогда активность ионов [Н ], а (Н ) =0,83∙0,178=0,148. Водородный показатель раствора НNO3ранен: рН = -lg а(Н ) = -lg 0,148=0,83.
Пример 4. Определение концентрации ионов Н и ОН— в растворах слабых кислот и оснований.
Концентрации [Н ] и [ОН—] ионов в растворах слабой кислоты и слабого основания могут быть вычислены, если известны их константы диссоциации. В общем виде формула для вычисления концентрации [Н ] в растворе слабой кислоты: [Н ]=√(Кдкислоты ∙ Скислоты)
Концентрация ионов [Н ]и [ОН—] в растворе слабого основания может быть вычислена по формуле: [ОН—]=√(Кдосн∙ Сосн.); [Н ]= Кв/[ОН—];
[Н ]=Кв/√(Кдосн∙Сосн).
Определите концентрацию[Н ], [ОН—], рН, рОН, в 0,0 М раствора муравьинной кислоты, если Кд(HCOOH)=2,1∙10-4
Решение:
[Н ]=√2,1∙10-4∙3∙10-2 = √6,3∙10-6= 2,5∙10-3 моль∙л-1;
рН= -lg 2,5∙10-3=3-lg 2,5 = 3-0,4= 2,6;
[ОН—]= Кв/[Н ]= 10-14/(2,5∙10-3)=4∙10-12 моль∙л-1;
рОН= 14-рН=14-2,6 = 11,4.
ГИДРОЛИЗ СОЛЕЙ
Под гидролизом понимают реакции обменного взаимодействия вещества с водой. Гидролиз является частным случаем сольволиза — обменного разложения растворенного вещества и растворителя. Процесс гидролиза в большинстве случаев обратим. Он происходит только в тех случаях, когда из ионов соли может образоваться хотя бы одно слабо диссоциирующее или труднорастворимое вещество. Образование такого вещества сопровождается связыванием одного из ионов, на которые диссоциирует вода, при этой происходит смещение равновесия этого процесса в сторону его усиления и изменение рН раствора. Различают три случая гидролиза.
1. Гидролиз по катиону. Характерен для солей, образованных слабым основанием и сильной кислотой (например, NН4Сl, Al(NO2)3, CuSO4 и другие). Рассмотрим гидролиз хлорида аммонияNН4Сl. Анонины Сl, образующиеся при диссоциации NН4Сl= NН4 Сl—не связывают ионов водорода, так как НС1 — сильная кислота. Катионы NН4 связывают ионы ОН— с образованием слабо диссоциирующего основания NН4СН по уравнению NН4 НОН  NН4ОН Н . При этом освобождаются ионы Н , обеспечивающие кислую реакцию среды (рН<7).
NН4ОН Н . При этом освобождаются ионы Н , обеспечивающие кислую реакцию среды (рН<7).
Молекулярное уравнение гидролиза записывается в виде
NН4Сl Н2О  NН4ОН НСl. Самым слабым электролитом в рассматриваемой системе является вода, поэтому равновесие смещено влево и гидролиз до конца не идет.
NН4ОН НСl. Самым слабым электролитом в рассматриваемой системе является вода, поэтому равновесие смещено влево и гидролиз до конца не идет.
2. Гидролиз по аниону, Характерен для солей, образованных сильным основанием и слабой кислотой (например, КCN, СН3СООNа, Na2CO3, K2S и др.).
Рассмотрим гидролиз ацетата натрия СН3СООNа. Рассуждая аналогично первому случаю, приходим к выводу, что в данной соли гидролизуется анион СН3СОО— по уравнению:
СН3СОО— НОН  СН3СООН ОН—
СН3СООН ОН—
Реакция среды щелочная (рН> 7).
Молекулярное уравнение реакции записывается следующим образом:
СН3СООNa Н2О  СН3СООН NaОН.
СН3СООН NaОН.
3. Гидролиз по аниону и катиону. Характерен для солей, образованных слабым основаниеми слабой кислотой.
Например, при гидролизе ацетата аммония NH4CH3COO и катион, и анион участвуют в процессе, образуя слабо диссоциирующие основание и кислоту:
NH4 CH3COO— НОН  NH4ОН CH3COOН.
NH4ОН CH3COOН.
В этом случае реакция среды определяется относительной силой (константой диссоциации) образующихся основания и кислоты. Если основание и кислота одинаковы по силе, то константы диссоциации их равны и рН=7; если кислота сильнее основания, т.е. константа ассоциации кислоты больше константы диссоциации основания, то реакция среды слабокислая, и наоборот.
В зависимости от основности слабой кислоты, образующей соль, и кислотности слабого основания различают две формы гидролиза: простейший и ступенчатый.
Простейший гидролиз. Характерен для солей, образованных одноосновной слабой кислотой и (или) слабым многокислотным основанием (NH4CN, NH4Cl, NaCl, CH3COONa, KNO2 и другие).
Ступенчатый гидролиз. Характерен для солей, образованных слабой многоосновной кислотой и (или) слабым многокислотным основанием (Na2CO3,K2S, (NH4)2,FeCL3,CuSO4,CuCL2 и другие).
Гидролиз по катиону. Рассмотрим гидролиз FеС13. Катионы Fе3 ,
образующиеся при диссоциации молекул соли FеСl3=Fe3 3Cl— связывают ионы ОН— с образованием слабодиссоциирующих частиц, причем присоединение гидроксильных групп происходит постепенно,
по ступеням:
1 ступень: Fе3 НОН  FеОН2 Н
FеОН2 Н
2 ступень: FeOH2 HOH  Fe(OH)2 H
Fe(OH)2 H
3 ступень: практически не протекает.
Накапливающиеся в системе ионы Н обеспечивают кислую реакцию среды и сильно смещают процесс диссоциации воды Н2О ↔ Н ОН—
влево, что приводит к ослаблению гидролиза на ступени 2, а по
ступени 3 гидролиз практически не идет.
Таким образом, гидролиз солей, образованных слабым многокислотным основанием и сильной кислотой, протекает ступенчато с образованием основных солей. Молекулярные уравнения:
1 ступень: FeCl3 H2O  FeOH2 H
FeOH2 H
2 ступень:FeOHCl2 H2O  Fe(OH)2Cl HCl
Fe(OH)2Cl HCl
3 ступень: практически не идет.
Гидролиз по аниону. Рассмотрим гидролиз соли Na2S. Анионы S2-, образующиеся при диссоциаций соли Na2S  2Na S2-, связывают ионы Н с образованием слабо диссоциирующих частиц. Присоединение Н происходит постепенно:
2Na S2-, связывают ионы Н с образованием слабо диссоциирующих частиц. Присоединение Н происходит постепенно:
1 ступень: S2- НОН  HS— OH—
HS— OH—
2 ступень: HS— HOH  H2S OH—
H2S OH—
Накапливающиеся в системе ионы OH— обеспечивают щелочную реакцию среды и ослабляют течение гидролиза по ступени 2.
Таким образом, гидролиз солей, образованных сильным основанием
и слабой многоосновной кислотой, протекает ступенчато с образованием кислых солей. Молекулярное уравнение:
1 ступень: Na2S H2O  NaHS NaOH
NaHS NaOH
2 ступень: практически не идет.
Полный необратимый гидролиз. Некоторые соли, образованные очень слабым основанием и слабой летучей кислотой (Cr2S3, Cr2(CO3)3, Fe2(CO3)3, Al2(CO3)3 и другие), подвергаются полному необратимому гидролизу. При этом образуется слабо диссоциирующие основание и кислота. Оба продукта уходят из сферы реакции в виде осадков и газов. Аналогично гидролизируются смеси солей, одна из которых образована очень слабым основанием и сильной кислотой, а другая — сильным основанием и слабой летучей кислотой (Na2S CrCl3 Na2CO3 Al2(SO4)3 и т.п.). Например:
2AlCl3 2Na2S 6H2O = 2Al(CO)3↓ 3H2S↑ 6NaCl
Количественными характеристиками процесса гидролиза служат степень и константа гидролиза.
Таблица 5
Примеры сильных и слабых кислот и оснований
| Кислоты | Основания | |||
| Сильные | Средней силы | Слабые | Сильные | Слабые |
| HCL | H3PO4 | HCN | Гидроксиды щелочных металлов (KOH, NaOH, ZiOH), Ba(OH)2 идр. | Na4OHи нерастворимые в воле основания (Ca(OH)2, Zi(OH)2, AL(OH)3 и др. |
| HBr | H2SO3 | HNO2 | ||
| HI | HP | H2CO3 | ||
| HNO3 | H2S | |||
| H2SO4 | CH3COOH | |||
| HMnO4 | HCIO | |||
| HCLO4 |
Константа гидролиза равна отношению произведения концентраций
продуктов гидролиза к концентрации негидролизованной соли.
Пример 1. Вычислить степень гидролиза NH4Cl.
Решение: Из таблицы находим Кд(NH4ОН)=1,8∙10-3, отсюда Кγ=Кв/Кдк= =10-14/1,8∙10-3= 5,56∙10-10.
Пример 2. Вычислить степень гидролиза ZnCl2 по 1 ступени в 0,5 М растворе.
Решение: Ионное уравнение гидролиза Zn2 H2O  ZnOH H
ZnOH H
KдZnOH 1=1,5∙10-9; hγ=√(Кв/ [Кдосн∙Cм]) = 10-14/1,5∙10-9∙0,5=0,36∙10-2 (0,36%).
Пример 3.Составьте ионно-молекулярные и молекулярные уравнения гидролиза солей: a) KCN; б) Na2CO3; в) ZnSO4. Определите реакцию среды растворов этих солей.
Решение, а) Цианид калия KCN — соль слабой одноосновной кислоты (см. табл. I приложения) HCN и сильного основания КОН. При растворении в воде молекулы KCN полностью диссоциируют на катионы К и анионы CN—. Катионы К не могут связывать ионы ОН— воды, так как КОН — сильный электролит. Анионы же CN— связывают ионы Н воды, образуя молекулы слабого элекролита HCN. Соль гидролизуется по аниону. Ионно-молекулярное уравнение гидролиза
CN— Н2О  HCN ОН—
HCN ОН—
или в молекулярной форме
KCN Н2О  HCN КОН
HCN КОН
В результате гидролиза в растворе появляется некоторый избыток ионов ОН—, поэтому раствор KCN имеет щелочную реакцию (рН > 7).
б) Карбонат натрия Na2CO3 — соль слабой многоосновной кислоты и сильного основания. В этом случае анионы соли СО32-, связывая водородные ионы воды, образуют анионы кислой соли НСО—3 , а не молекулы Н2СО3, так как ионы НСО—3 диссоциируют гораздо труднее, чем молекулы Н2СО3. В обычных условиях гидролиз идет по первой ступени. Соль гидролизуется по аниону. Ионно-молекулярное уравнение гидролиза
CO2-3 H2O  HCO—3 ОН—
HCO—3 ОН—
или в молекулярной форме Na2CO3 Н2О  NaHCO3 NaOH
NaHCO3 NaOH
В растворе появляется избыток ионов ОН—, поэтому раствор Na2CO3 имеет щелочную реакцию (рН > 7).
в) Сульфат цинка ZnSO4 — соль слабого многокислотного основания Zn(OH)2 и сильной кислоты H2SO4. В этом случае катионы Zn связывают гидроксильные ионы воды, образуя катионы основной соли ZnOH .Образование молекул Zn(OH)2 не происходит, так как ионы ZnOН диссоциируют гораздо труднее, чем молекулы Zn(OH)2. В обычных условиях гидролиз идет по первой ступени. Соль гидролизуется по катиону. Ионно-молекулярное уравнение гидролиза
Zn2 Н2О  ZnOН Н
ZnOН Н
или в молекулярной форме
2ZnSO4 2Н2О  (ZnOH)2SO4 H2SO4
(ZnOH)2SO4 H2SO4
В растворе появляется избыток ионов водорода, поэтому раствор ZnSO4 имеет кислую реакцию (рН < 7).
Пример 4.Какие продукты образуются при смешивании растворов A1(NO3)3 и К2СО3? Составьте ионно-молекулярное и молекулярное уравнение реакции.
Решение. Соль A1(NO3)3 гидролизуется по катиону, а К2СО3 — по аниону:
А13 Н2О  А1ОН2 Н
А1ОН2 Н
СО2-3 Н2О  НСО— з ОН—
НСО— з ОН—
Если растворы этих солей находятся в одном сосуде, то идет взаимное усиление гидролиза каждой из них, ибо ионы Н и ОН—образуют молекулу слабого электролита Н2О. При этом гидролитическое равновесие сдвигается вправо и гидролиз каждой из взятых солей идет до конца с образованием А1(ОН)3 и СО2 (Н2СО3). Ионно-молекулярное уравнение:
2А13 ЗСО2-3 ЗН2О = 2А1(ОН)3 ЗСО2
молекулярное уравнение: ЗСО2 6KNO3
2A1(NO3)3 ЗК2СО3 ЗН2О = 2А1(ОН)3
§
Гетерогенное равновесие «осадок ↔ насыщенный раствор» подчиняется правилу произведения растворимости. Если малорастворимый
электролит диссоциирует по уравнению AmBn  [А ]m — [B—]n. Отсюда вытекают два следствия:
[А ]m — [B—]n. Отсюда вытекают два следствия:
1. Условие растворения осадка. Произведение концентраций ионов, возведенных в степень стехиометрических коэффициентов, должно быть меньше величины произведения растворимости:[А ]m[B—]n<ПР (AmBn).
2. Условие осаждения осадка. Произведение концентраций ионов,
возведенных в степень их стехиометрических коэффициентов, должно
быть больше величины произведения растворимости: [А ]m[B—]n>Пр(AmBn).
Пример 1. Определение условий выпадения осадка. Образуется ли осадок СаСО3 при смешивании равных объемов 0,02 М растворов хлористого кальция и углекислого натрия? (Пр(СаСО3) = 1,0∙10-3)
Решение: При смешении равных объемов растворов CaCI2 и Na2CO3объем смеси увеличивается в 2 раза, а концентрация каждого из ионов уменьшается в 2 раза. Следовательно,
[CaCI2]= [Ca 2] = 0,02∙0,5=1∙10-2 моль∙л-1.
[Na2CO3] = [CО32-] = 0,2∙0,5 = 1∙10-2 моль∙л-1.
Откуда [Ca 2]∙[CО32-]= 1∙10-2 ∙1∙10-2 = 1∙10-4 . Осадок образуется, так как 1,0∙10-3< 1∙10-4
Пример 2. Вычисление концентрации ионов малорастворимого электролита в его насыщенном растворе.
Произведение растворимости BaF2 при 18 º С равно 1,7∙106. Рассчитайте концентрацию ионов Ba 2 и F— в насыщенном растворе BaF2 при этой температуре.
Решение: BaF2 диссоциирует по уравнению BaF2 Ba 2 2F—. При диссоциации BaF2 ионов F-1 получается в 2 раза больше, чем ионов Ba 2. Следовательно, [F-1] = 2[Ва 2]. Произведение растворимости соли ПР (BaF2) = [Ва 2]∙[F ]. Выразим концентрацию ионов Ва 2, тогда
Ba 2 2F—. При диссоциации BaF2 ионов F-1 получается в 2 раза больше, чем ионов Ba 2. Следовательно, [F-1] = 2[Ва 2]. Произведение растворимости соли ПР (BaF2) = [Ва 2]∙[F ]. Выразим концентрацию ионов Ва 2, тогда
ПР (BaF2) = [Ва 2] ∙ 2∙ [Ва 2]2 = 4[Ва 2]3= 1,7∙10-6
Концентрация ионов [Ва 2] равна: [Ва 2]= √1,7∙10-6 / 4 = 0,75∙10-2 моль∙л-1;
Концентрация ионов F-1 равна: [F-1]=0,75∙10-2∙2=1,5∙10-2 моль∙л-1;
Пример 3. Вычисление произведения растворимости малорастворимого электролита.
Растворимость Ag3PO4в воде при 20 º С равна 0,0065 г∙л-1. Рассчитайте значение произведения растворимости.
Решение. Растворимость Ag3PO4 в моль∙л-1 равна:
Р=6,5∙10-3/418,58 = 1,6∙10-5 моль∙л-1.
При диссоциации 1 моль Ag3PO4образует 3 моль ионовAg . 1 моль ионов PO43-, поэтому концентрация ионов PO43- равна растворимости Ag3PO4, а концентрация иона Ag в 3 раза больше, т.е.
С[PO43-] =1,6∙10-5моль∙л-1. [Ag ]= 3∙1,6∙10-5. Произведение растворимости Ag3PO4равно:
ПР=[Ag ]3 [PO43-]= (4,8∙10-5)3∙1,6∙10-5= 110,6 ∙10-15∙1,6∙10-3= 1,77∙10-18.
Пример 4. Определение условий одновременного выпадения осадков солей из раствора.
При каком соотношении концентрации ионов Zn 2Cd 2 в растворе прибавление к нему раствора Na2CO3вызывает одновременное осаждение карбонатов этих ионов? ПР(ZnCOз)= 6∙10-11
Решение. Концентрацию вводимых карбонат-ионов обозначим через
[СО32- ], тогда
[Zn 2]=ПР(ZnCOз) / С(СО32-), [Cd 2] = ПР (CdСОз)/[СО32- ].
[Zn 2]/[Cd 2] = ПР(ZnCOз)/ПР (CdСОз)=6∙10-11/2,5∙10-14=2,4∙103=2400
Карбонаты цинка и кадмия будут выпадать одновременно из раствора, если [Zn 2] >[Cd 2] в 2400 раз. Если отношение [Zn 2] /[Cd 2] > 2400, то первым из раствора будет выпадать ZnCOз до тех пор, пока отношение [Zn 2] /[Cd 2] не будет равным 2400. И только после этого начнется одновременное выпадение осадков. Если же отношение концентрации ионов цинка и кадмия меньше 2400, то первым начнет осаждаться карбонат кадмия. Осаждение карбоната кадмия будет протекать до тех пор, пока отношение [Zn 2] /[Cd 2] не достигнет значения, при котором ZnCOз и CdСОз будут осаждаться одновременно.
Пример 5. Вычисление растворимости электролита по величине
произведения растворимости.
Произведение растворимости ПР оксалата бария ВаС2О4 равно
1,62∙10-1. Вычислите растворимость ВаС2О4 в воде.
Решение. В растворе труднорастворимого сильного электролита
ВаС2О4 существует равновесие: ВаС2О4= Ва 2 (С2О42-).
ПрВаС2О4= [Ва 2] ∙ [С2О42-]
в осадке в растворе
Так как оксалат бария диссоциирует на два иона, то концентрация его в растворе равна концентрации каждого из ионов, т.е.
[ВаС2О4] = [Ва 2] = [С2О42-] = √1,62∙10-7 = 0,4∙10-3моль-л-1.
т.е. растворимость оксалата бария в воде при t =20°С равна 0,4∙10-3моль-л-1.
ЖЕСТКОСТЬ ВОДЫ
В природной воде содержатся различные по растворимости соли.
Если в воде содержится большое количество солей кальция или магния, то такая вода называется жесткой в отличие от мягкой воды,
в которой таких солей мало или они отсутствуют. Суммарное содержание в воде солей кальция и магния называется общей жесткостью.
Она подразделяется на карбонатную и некарбонатную.
Карбонатная жесткость обусловлена содержанием гидрокарбонатов
кальция и магния; некарбонатная — содержанием сульфатов или хлоридов кальция и магния.
Вода, обладающая карбонатной жесткостью, при кипячении дает
осадок, состоящий в основном из карбоната кальция СаСО3
Са(НСС3)2 → СаСО3↓ СО2↑ Н2О
Карбонатная жесткость относится к временной жесткости, количественно она характеризуется содержанием гидрокарбонатов, удаляющихся при кипячении воды в течение одного часа. Жесткость, остающаяся посте такого кипячения, называется постоянной жесткостью.
Сумма миллиэквивалентов ионов магния и кальция, содержащаяся
в 1 литре воды, определяет ее жесткость. Один миллиэквивалент жесткости соответствует содержанию 20,04 мг/л [Са2 ] или 12,16 мг/л [Mg2 ].Жесткость природной воды в разных водоемах различна и колеблется в течение года. Из Европейских рек наибольшую жесткость воды имеет Волга (общая — 5,9; карбонатная — 3,5 ткь/я), наименьшую — Нева (общая0,5; карбонатная — 0,5 мэкв/л). Жест кость Москвы-реки — общая — 4,2, карбонатная 4,1 мэкв/л.
Жесткая вода непригодна для технических целей, Для уменьшения
жесткости используют методы водоумягчения:
— осаждение катионов Са2 и Mg2 кипячением или добавлением
химических реагентов ( Na2CO3) ;
— ионный обмен (воду пропускают последовательно через слой
катионита и слой анионита).
Пример 1. Вычислите жесткость воды, зная, что в 500 л ее со-
держится 202,5 г Са(НСОз)2.
Решение. В 1л воды содержится 202,5 : 500 = 0,405 г Са(НСОз)2 ,
что составляет 0,405 : 81 = 0,005 эквивалентных масс или 5 мэкв/л.
81 г/моль — эквивалентная масса Са(НСОз)2. Следовательно, жесткость воды 5 мкэв.
Пример 2. Сколько граммов CaSO4 содержится в 1 м3 воды, если
жесткость, обусловленная присутствием этой соли, равна 4 мэкв?
Решение: Мольная масса CaSO4=136,14 г/моль; эквивалентная
масса равна 136,14/2=63,07 г/моль. В в 1 м3 воды жесткостью 4 мэкв содержится 4∙1000=4000 мэкв, или 4000∙68,07= 272280 мг= 272,280 г CaSO4 .
Пример 3. Какую массу соды надо добавить к 500 л воды, чтобы
устранить ее жесткость равную 5 мквэ?
Решение. В 500 л вода содержится 530 ∙ 5 = 2500 мквэ солей, обусловливающих жесткость воды. Для устранения жесткости следует
прибавить 2500 ∙ 53 = 132 500 мг = 132,5 г соды (53 г/моль — эквивалентная масса Na2CO3).
Пример 4. Вычислите карбонатную жесткость воды, зная, что натитрование 100 см3 этой воды, содержащей гидрокарбонат кальция,
потребовалось 6,25 см3 0,08 н. раствора НС1.
Решение. Вычисляем нормальность раствора гидрокарбоната кальция. Обозначив число эквивалентов растворенного вещества в 1 л раствора, т.е. нормальность, через х, составляем пропорцию.
6,25/100=х/0,08, х= 0,005.
Таким образом, в 1 л исследуемой воды содержится 0,005∙1000 = 5 мэкв гидрокарбоната кальция или 5 мэквСа2 ионов. Карбонатная жесткость воды 5 мэкв. Приведенные примеры решают, применяя формулу Ж =m/ЭV, где m- масса вещества, обусловливающего жесткость воды или применяемого для устранения жесткости воды, мг; Э — эквивалентная масса этого вещества; V — объем воды, л.
Решение примера 1. Ж =m/ЭV=202500/81∙500=5 мэкв. 81 — эквивалентная масса Ca(HCO3)2, равная половине его мольной массы.
Решение примера 2. Из формулыЖ =m/ЭV, m = 4∙68,07∙1000=272280 мг = 272,280 г. CaSO4.
§
Окислительно-восстановительными называют реакции, сопровождающиеся изменением степени окисления атомов, входящих в состав реагирующих веществ. Под степенью окисления (п) понимают условный заряд атома, который вычисляют исходя из предположения, что молекула состоит только из ионов. Иными словами: степень окисления — это условный заряд, который приобрел бы атом элемента, если предположить, что они принял или отдал то или иное число электронов.
Окисление-восстановление — это единый, взаимосвязанный процесс. Окисление приводит к повышению степени окисления восстановителя, а восстановление — к ее понижению у окислителя.
Повышение или понижение степени окисления атомов отражается в электронных уравнениях: окислитель принимает электроны, а восстановитель их отдает. При этом не имеет значения, переходят ли электроны от одного атома к другому полностью и образуются ионные связи или электроны только оттягиваются к более электроотрицательному атому и возникает полярная связь. О способности того или иного вещества проявлять окислительные, восстановительные или двойственные (как окислительные, так и восстановительные) свойства можно судить по степени окисления атомов окислителя и восстановителя.
Атом того или иного элемента в своей высшей степени окисления не может ее повысить (отдать электроны) и проявляет только окислительные свойства, а в своей низшей степени окисления не может ее понизить (принять электроны) и проявляет только восстановительные свойства. Атом же элемента, имеющий промежуточную степень окисления, может проявлять как окислительные, так и восстановительные свойства.Например:
| N5 (HNO3) | S6 (H2SO4) | Проявляют только окислительные свойства |
| N4 (NO2) | S4 (SO2) | Проявляют окислительные и восстановительные свойства |
| N3 (NH2) | ||
| N2 (NO) | S2 (SO) | |
| N (N2O) | ||
| N0(N2) | S0(S2; S8) | |
| N—(NH2OH) | S-1(H2S2) | |
| N2-(N2H4) | ||
| N3-(NH3) | S2-(H2S) | Проявляют только восстановительные свойства |
При окислительно-восстановительных реакциях валентность атомов может и не меняться. Например, в окислительно-восстановительной реакции Н°2 С1°2= 2Н Сl— валентность атомов водорода и хлора до и после реакции равна единице. Изменилась их степень окисления. Валентность определяет число связей, образованных данным атомом, и поэтому знака заряда не имеет. Степень же окисления имеет знак плюс или минус.
Пример 1.Исходя из степени окисления (п) азота, серы и марганца в соединениях NH3, HNO2, HNO3, H2S, H2SO3, H2SO4, MnO2 и KMnO4, определите, какие из них могут быть только восстановителями, только окислителями и какие проявляют как окислительные, так и восстановительные свойства.
Решение. Степень окисления азота в указанных соединениях соответственно равна: -3 (низшая), 3 (промежуточная), 5 (высшая); n(S) соответственно равна: -2 (низшая), 4 (промежуточная), 6 (высшая); л(Мn) соответственно равна: 4 (промежуточная), 7 (высшая). Отсюда: NH3, H2S — только восстановители; HNO3, H2SO4, КМnО4 — только окислители; HNO2, H2SO3, MnO2 — окислители и восстановители.
Пример 2.Могут ли происходит окислительно-восстановительные реакции между следующими веществами: a) H2S и HI; б) H2S и H2SO3; в) H2SO3 и НС1О4?
Решение, а) Степень окисления в H2S w(S) = -2; в HI и(1) = -1. Так как и сера, и иод находятся в своей низшей степени окисления, то оба вещества проявляют только восстановительные свойства и взаимодействовать друг с другом не могут; б) в H2S n(S) = -2 (низшая), в H2SO3 n(S) = 4 (промежуточная).
Следовательно, взаимодействие этих веществ возможно, причем H2SO3 является окислителем;
в) в H2SO3 n(S) = 4 (промежуточная); в НС1О4 n(С1) = 7 (высшая). Взятые вещества могут взаимодействовать, H2SO3 в этом случае будет проявлять восстановительные свойства.
Пример 3.Составьте уравнения окислительно-восстановительной реакции, идущей по схеме:
7 3 2 5
KMnO4 H3PO3 H2SO4→MnSO4 Н3РО4 K2SO4 Н2О
Решение. Если в условии задачи даны как исходные вещества, так и продукты их взаимодействия, то написание уравнения реакции сводится, как правило, к нахождению и расстановке коэффициентов. Коэффициенты определяют методом электронного баланса с помощью электронных уравнений. Вычисляем, как изменяют степень окисления восстановитель и окислитель, и отражаем это в электронных уравнениях:
восстановитель 5 Р3 — 2е— = Р5 процесс окисления
окислитель 2 Мn7 5е—= Мn2 процесс восстановления
Общее число электронов, отданных восстановителем, должно быть равно числу электронов, которые присоединяет окислитель. Общее наименьшее кратное для отданных и принятых электронов десять. Разделив это число на 5, получаем коэффициент 2 для окислителя и продукта его восстановления, а при делении 10 на 2 получаем коэффициент 5 для восстановителя и продукта его окисления. Коэффициент перед веществами, атомы которых не меняют свою степень окисления, находят подбором. Уравнение реакции будет иметь вид
2КМnО4 5Н3РО3 3H2SO4 = 2MnSO4 5Н3РО4 K2SO4 ЗН2О
Пример 4.Составьте уравнение реакции взаимодействия цинка с концентрированной серной кислотой, учитывая максимальное восстановление последней.
Решение. Цинк, как любой металл, проявляет только восстановительные свойства. В концентрированной серной кислоте окислительная функция принадлежит сере ( 6). Максимальное восстановление серы означает, что она приобретает минимальную степень окисления. Минимальная степень окисления серы как p-элемента VIA-группы равна -2. Цинк как металл IIВ-группы имеет постоянную степень окисления 2. Отражаем сказанное в электронных уравнениях:
восстановитель Zn — 2e—= Zn2 процесс окисления
окислитель S6 8е— = S2-процесс восстановления
Составляем уравнение реакции:
4Zn 5H2SO4 = 4ZnSO4 H2S 4H2O
Перед H2SO4 стоит коэффициент 5, а не 1, ибо четыремолекулы H2SO4 идут на связывание четырех ионов Zn2 .
§
Если металлическую пластинку опустить в воду, то катионы металла на ее поверхности гидратируются полярными молекулами воды и переходят в жидкость. При этом электроны, в избытке остающиеся в металле, разряжают его поверхностный слой отрицательно. Возникает электростатическое притяжение между перешедшими в жидкость гидратированными катионами и поверхностью металла. В результате этого в системе устанавливается подвижное равновесие:
Ме m Н2О  Ме(Н2О) n m ne—
Ме(Н2О) n m ne—
в растворе на металле
где n — число электронов, принимающих участие в процессе.
На границе металл — жидкость возникает двойной электрический слой, характеризующийся определенным скачком потенциала — электродным потенциалом. Абсолютные значения электродных потенциалов измерить не удается. Электродные потенциалы зависят от ряда факторов (природы металла, концентрации, температуры и др.). Поэтому обычно определяют относительные электродные потенциалы в определенных условиях — так называемые стандартные электродные потенциалы (Е°).
Стандартным электродным потенциалом металла называют его электродный потенциал, возникающий при погружении металла в раствор собственного иона с концентрацией (или активностью), равной 1 моль/л, измеренный по сравнению со стандартным водородным электродом, потенциал которого при 25°С условно принимается равным нулю (Е°=0;∆G0= 0).
Располагая металлы в ряд по мере возрастания их стандартных электродных потенциалов (Е0), получаем ряд стандартных электродных потенциалов (ряд напряжений).
Положение того или иного металла в ряду стандартных электродных потенциалов (ряд напряжений) характеризует его восстановительную способность, а также окислительные свойства его ионов в водных растворах при стандартных условиях. Чем меньше значение Е°, тем большими восстановительными способностями обладает данный металл в виде простого вещества и тем меньшие окислительные способности проявляют его ионы, и наоборот. Электродные потенциалы измеряют приборами, которые называют гальваническими элементами. Окислительно-восстановительная реакция, которая характеризует работу гальванического элемента, протекает в направлении, в котором ЭДС элемента имеет положительное значение. В этом случае ∆G0 < 0, так как ∆G 0= — nFE0.
Пример 1. Стандартный электродный потенциал никеля больше, чем кобальта (табл. 8). Изменится ли это соотношение, если измерить потенциал никеля в растворе его ионов с концентрацией 0,001 моль/л, а потенциалы кобальта — в растворе с концентрацией 0,1 моль/л.
Решение. Электродный потенциал металла (Е) концентрации его ионов в растворе. Эта зависимость уравнением Нернста: 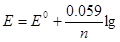 с,
с,
где Е° — стандартный электродный потенциал; и — число электронов, принимающих участие в процессе; с — концентрация (при точных вычислениях — активность) гидратированных ионов металла в растворе, моль/л; Е0— для никеля и кобальта соответственно равны -0,25 и -0,277 В. Определим электродные потенциалы этих металлов при заданных концентрациях:
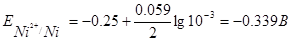
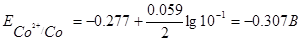
Таким образом, при изменившейся концентрации потенциал кобальта стал больше потенциала никеля.
Пример 2. Магниевую пластинку опустили в раствор его соли. При этом электродный потенциал магния оказался равен -2.41 В. Вычислите концентрацию ионов магния (в моль/л).
Решение. Подобные задачи также решаются на основании уравнения Нернста (см. пример 1): 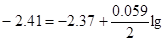 с ; -0,04=0,0295lg c?
с ; -0,04=0,0295lg c?
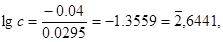
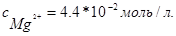
Таблица 8
Стандартные электронные потенциалы(∆Е0) некоторых металлов
| Электрод | Е0, В | Электрод | Е0, В |
| Li / Li | -3.045 | Cd2 /Cd | -0.403 |
| Rb / Rb | -2.925 | Co2 /Co | -0.277 |
| K /K | -2.924 | Ni2 /Ni | -0.25 |
| Cs /Cs | -2.923 | Sn2 / Sn | -0.136 |
| Ba2 /Ba | -2.90 | Pb2 /Pb | -0.127 |
| Ca2 /Ca | -2.87 | Fe3 /Fe | -0.037 |
| |Na /Na | -2.714 | 2H /H2 | -0.000 |
| Mg2 /Mg | -2.37 | Sb3 /Sb | 0.20 |
| Al3 /Al | -1.70 | Bi3 /Вi | 0.215 |
| Ti2 /Ti | -1.603 | Cu2 /Сu | 0.34 |
| Zr4 /Zr | -1.58 | Cu /Cu | 0.52 |
| Mn4 /Mn | -1.18 | Hg2 2/2Hg | 0.79 |
| V2 /V | -1.18 | Ag /Ag | 0.80 |
| Cr2 /Cr | -0.913 | Hg2 /Hg | 0.85 |
| Zn2 /Zn | -0.763 | Pt2 /Pt | 1.19 |
| Cr3 /Cr | -0.74 | Au3 /Au | 1.50 |
| Fe2 /Fe | -0.44 | Au /Au | 1.70 |
Пример З.Составьте схему- гальванического элемента, в котором электродами являются магниевая и цинковая пластинки, опущенные в растворы их ионов с активной концентрацией 1 моль/л. Какой металл является анодом, какой катодом? Напишите уравнение окислительно-восстановительной реакции, протекающей в этом гальваническом элементе, и вычислите его ЭДС.
Решение. Схема данного гальванического элемента
(-) Mg | Mg2 || Zn2 | Zn ( )
Вертикальная линейка обозначает поверхность раздела между металлом и раствором, а две линейки — границу раздела двух жидких фаз — пористую перегородку (или соединительную трубку, заполненную раствором электролита). Магний имеет меньший потенциал (-2,37 В) и является анодом, на котором протекает окислительный процесс:
Mg°-2e- = Mg2 (1)
Цинк, потенциал которого -0,763 В, — катод, т.е. электрод, на котором протекает восстановительный процесс:
Zn2 2е~ = Zn° (2)
Уравнение окислительно-восстановительной реакции, характеризующее работу данного гальванического элемента, можно получить, сложив электронные уравнения анодного (1) и катодного (2) процессов:
Mg Zn2 = Mg2 Zn
Для определения ЭДС гальванического элемента из потенциала катода следует вычесть потенциал анода. Так как концентрация ионов в растворе 1 моль/л, то ЭДС элемента равна разности стандартных потенциалов двух его электродов:
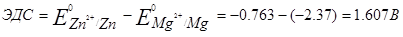
Электролиз
Пример 1.Какая масса меди выделится на катоде при электролизе раствора CuSO4 в течение 1 ч. При силе тока 4А? Решение. Согласно законам Фарадея
m = ЭIt/96500, (1)
где т — масса вещества, окисленного или восстановленного на электроде; Э — молярная масса эквивалента вещества; I — сила тока, A; t — продолжительность электролиза, с.
Молярная масса эквивалентов меди в CuSO4 равна 63,54 : 2 = =31,77 г/моль. Подставив в формулу (1) значения Э = 31,77, I = 4 А, t= 60 ∙ 60 = 3600 с, получим
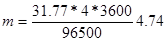
Пример 2.Вычислите молярную массу эквивалента металла, зная, что при электролизе раствора хлорида этого металла затрачено 3880 Кл электричества и на катоде выделяется 11,742 г металла.
Решение. Подставляя в формулу (1) числовые значения, получаем
Э = 11,742 ∙ 96500/3880 = 29,35 г/моль,
где m = 11,742 г; It = Q = 3880 Кл.
Пример 3.Чему равна сила тока при электролизе раствора в течение 1 ч 40 мин 25 с, если на катоде выделилось 1,4 л водорода (н.у.)?
Решение. Из формулы (1)
I = m 96500/Эt
Так как дан объем водорода, то отношение т/Э заменяем отношением VH; /VЭ(Н  ), где VH
), где VH  — объем водорода, л.; VЭ(Н
— объем водорода, л.; VЭ(Н  ) объем эквивалентной массы водорода, л. Тогда
) объем эквивалентной массы водорода, л. Тогда
I = VH  96500/ VЭ(Н
96500/ VЭ(Н  ).
).
Объем эквивалентной массы водорода при н.у. равен половине молярного объема 22,4/2 = 11,2 л. Подставив в приведенную формулу значения VН  = 1,4 л, VЭ(Н
= 1,4 л, VЭ(Н  )= 11,2 л, t = 6025 (1 ч 40 мин 25 с=6025с), находим
)= 11,2 л, t = 6025 (1 ч 40 мин 25 с=6025с), находим
I = 1,4∙96,500/(11.2*6025) = 2А
Пример 4.Какая масса гидроксида калия образовалась у катода при электролизе раствора K2SO4, если на аноде выделилось 11,2 л кислорода (н.у.)?
Решение. Объем эквивалентной массы кислорода (н.у.) 22,4/4 = = 5,6 л. Следовательно, 11,2 л содержат две молярные массы эквивалента кислорода. Столько же эквивалентных масс КОН образовалось у катода, или 56,11 ∙ 2 = 112,22 г (56,11 г/моль — молярная и эквивалентная масса КОН).
8.3Коррозия металлов
При решении задач этого раздела см. табл. 8.
Коррозия — это самопроизвольно протекающий процесс разрушения металлов в результате химического или электрохимического взаимодействия их с окружающей средой.
При электрохимической коррозии на поверхности металлаодновременно протекают два процесса: анодный — окисление металла
Ме°-пе=Меп и катодный — восстановление ионов водорода
2Н 2е = Н2
или молекул кислорода, растворенного в воде,
О2 2Н2О 4е- = 4ОН—
Ионы или молекулы, которые восстанавливаются на катоде, называют деполяризаторами. При атмосферной коррозии — коррозии во влажном воздухе при комнатной температуре — деполяризатором является кислород [1].
Пример 1.Как происходит коррозия цинка, находящегося в контакте с кадмием в нейтральном и кислом растворах. Составьте электронные уравнения анодного и катодного процессов. Каков состав продуктов коррозии?
Решение. Цинк имеет более отрицательный потенциал (-0,763 В), чем кадмий (-0,403 В), поэтому он является анодом, а кадмий катодом.
Анодный процесс:
Zn°-2e—=Zn2 катодный процесс:
в кислой среде 2Н 2е—= Н2
в нейтральной среде ½ О2 Н2О 2е—= 2ОН—
Так как ионы Zn2 с гидроксильной группой образуют нерастворимый гидроксид, то продуктом коррозии будет Zn(OH)2.
§
Основные понятия
Кристаллическое состояние веществ — одно из самых распространенных в окружающей нас природе. Кристаллическими являются очень многие синтетические материалы, используемые в современной технике: полупроводники, ферромагнетики, сверхпрочные и жаростойкие сплавы. В связи с этим изучение кристаллического состояния является делом первостепенной научной важности.
Каковы основные признаки кристаллического состояния? Твердое вещество существует в двух формах: оно может быть кристаллическим или аморфным. Одно из характерных свойств кристаллического вещества, в отличие от аморфного, — это способность самоограняться. Кристаллы образуются по-разному: они выпадают в осадок при упаривании раствора, возникают при охлаждении расплава, при достаточно низкой температуре, они растут из паров (иней или морозные узоры на стекле). И во всех этих случаях на поверхности кристаллов самопроизвольно возникают плоские грани.
Вместе с тем, огранка — хотя и характерный, но не обязательный признак кристаллического вещества. В некоторых случаях грани кристаллов бывают выражены весьма нечетко. Иногда вещество состоит из таких мелких кристалликов, что грани трудно обнаружить даже под микроскопом. Кроме того, если кристалл обточить, придав ему округлую форму, лишенную граней, вещество не перестанет быть кристаллическим и свойства его останутся прежними.
Способность самоограняться — это лишь одно из проявлений более общего, наиболее важного качества кристаллов — их анизотропии (различие свойств по разным направлениям).
Если из кристалла поваренной соли, имеющего форму куба, выточить шар, а затем погрузить его в насыщенный раствор соли и медленно упаривать раствор, то кристалл начнет расти и постепенно снова примет форму куба. Этот опыт показывает, что скорость роста кристалла в разных направлениях неодинакова. Грани кристалла возникают перпендикулярно направлениям, по которым скорость роста минимальна.
Анизотропия проявляется в очень многих физических свойствах кристаллов. В отличие от кристаллических, аморфные вещества, имеющие совершенно одинаковые свойства по всем направлениям, называют изотропными. В этом отношении они подобны жидкостям и газам.
Еще одна характерная особенность кристаллов — фиксированная температура плавления. При нагревании кристаллическое вещество до определенной температуры остается твердым, а затем начинает плавиться, переходя в жидкое состояние. Пока продолжается плавление, температура не повышается. Аморфные вещества ведут себя иначе. При нагревании куска стекла он начинает постепенно размягчаться и, наконец, растекается, принимая форму сосуда. Невозможно установить, при какой температуре это произошло. Вязкость стекла уменьшается постепенно, никакой остановки в росте температуры нет.
Но самая важная особенность кристаллического вещества заключается в упорядоченном расположении его атомов.
На рисунке 2 показано внутреннее строение кристалла (а) и аморфного вещества (б) того же состава.
Рис 2. Внутренне строение кристаллического вещества
Рисунок имеет условный характер, так как в действительности атомы вещества располагаются не на плоскости, а в пространстве. Рассмотрим атомы, обозначенные черными точками. В обоих случаях окружение каждого из таких атомов почти одинаково: ближайшие соседи располагаются по вершинам треугольника, совершенно правильного при кристаллическом и почти правильного при аморфном состоянии. Значит, и в аморфном веществе имеется так называемый «ближний порядок». Но если принять во внимание не только самых близких соседей, то выяснится, что в кристалле окружение каждого атома остается одинаковым, а в аморфном веществе оно окажется разным. Поэтому говорят, что в кристаллическом теле, в отличие от аморфного, наблюдается «дальний» порядок. Следствием этого являются все особые свойства кристаллов. Естественно, что в направлении АВ, параллельном направлению некоторых связей между атомами, свойства будут не такими, как в направлении CD, вдоль которого такие связи не проходят. В аморфном веществе подобных специфических направлений мы не найдем. Так объясняется анизотропия кристаллов, в частности различная скорость роста в различных направлениях, а следовательно, и способность самоограняться.
В приведенном примере мы рассматривали вещество, которое может существовать и в аморфном и в кристаллическом состоянии. Это действительно так. При быстром охлаждении расплавленного сахара получается аморфная масса (леденец), при медленном охлаждении в образующемся твердом сахаре можно заметить поблескивающие кристаллики.
Нетрудно понять, почему так происходит. Представим себе роту солдат, которым приказано строиться. Если им дать для этого хотя бы немного времени, они успеют занять свои места, выровнять ряды. Если же после команды «строиться» будет сразу подана команда «стой», то расположение солдат так и останется беспорядочным, хотя, может быть, и наметится какая-то тенденция к порядку. Нечто подобное происходит и при затвердевании: если процесс идет медленно, частицы успевают занять отведенные им места, быстрое затвердевание не дает им такой возможности.
Но даже в твердом аморфном веществе, хотя и очень медленно, атомы перемещаются и постепенно упорядочивают свое расположение. Леденец, пролежав несколько месяцев, начинает кристаллизоваться «засахариваться». Старинное стекло иногда мутнеет — в нем образуется множество мельчайших кристалликов и возникающая неоднородность материала приводит к потере прозрачности.
Аморфное вещество самопроизвольно переходит в кристаллическое, а вот противоположный процесс никогда не наблюдается. Отсюда следует очень важный вывод: кристаллическое состояние — это равновесное, наиболее устойчивое состояние твердого вещества.
§
 Классификация кристаллов основана на их симметрии. Тот или иной объект обладает симметрией, если после определенного изменения его положения в пространстве он совмещается со своим первоначальным положением. Так, трехлопастный пропеллер можно повернуть вокруг оси на 120° (на одну треть оборота), и тогда его положение нельзя отличить от первоначального при условии, что все лопасти совершенно одинаковы.
Классификация кристаллов основана на их симметрии. Тот или иной объект обладает симметрией, если после определенного изменения его положения в пространстве он совмещается со своим первоначальным положением. Так, трехлопастный пропеллер можно повернуть вокруг оси на 120° (на одну треть оборота), и тогда его положение нельзя отличить от первоначального при условии, что все лопасти совершенно одинаковы.

Рис. 3 Виды симметрии кристалла
Точно так же он может быть повернут на 240° (на две трети оборота), и снова невозможно будет отличить его новое положение от первоначального. Такое вращение на одну треть оборота, на две трети оборота, а также полный оборот образуют операции симметрии, характерные для оси симметрии третьего порядка. Некоторые другие примеры симметрии показаны на рисунке 3.
Кристаллы обладают лишь некоторыми элементами симметрии, к числу которых относятся: центр симметрии, оси симметрии второго порядка, третьего порядка, четвертого порядка, шестого порядка, зеркально-поворотные оси четвертого и третьего порядка, плоскость симметрии. Все эти виды симметрии показаны на рисунке 4.
Ось симметрии пятого порядка в кристаллах не встречается, поскольку угол пятиугольника равен 108°, а на такое число не делиться угол 360°.
Существует 32 сочетания элементов симметрии, свойственных кристаллам. Эти сочетания называются видами симметрии или классами кристаллов. Описание видов симметрии кристаллов можно найти в руководствах по кристаллографии. Тридцать два вида (класса) симметрии кристаллов разделяются на шесть систем или сингоний кристаллов:
1) кубическая система (иногда называемая изометрической) с осями симметрии третьего и четвертого порядка (оси четвертого порядка могут быть зеркально-поворотного типа);
2) тетрагональная система с одной осью четвертого порядка;
3) гексагональная или тригональная система (включает ромбоэдрические кристаллы) с одной осью шестого порядка или одной осью третьего порядка;
Рис. 4 Виды симметрии кристалла
4) ромбическая система с двумя или тремя плоскостями сим
метрии или осями симметрии второго порядка, образующими прямые углы между собой;
5) моноклинная система с одной плоскостью или одной осью второго порядка, или же с тем и другим элементом симметрии;
6) триклинная система с центром симметрии или без элементов симметрии.
Кристаллы и их элементарные ячейки можно описать осями симметрии, которые в одних случаях могут располагаться под прямыми углами одна к другой, в других под углами 120° (в случае гексагональной и тригональной систем), или под другими углами. Различным системам свойственны следующие типы осей:
кубической системе: три равные взаимно перпендикулярные оси длиной а;
тетрагональной системе: две равные оси длиной а и третья ось длиной с; все оси взаимно перпендикулярны;
гексагональной или тригональной системе: две равные оси длиной а образуют между собой угол 120°, третья ось длиной с расположена под прямым углом к первым двум:
ромбической системе: три оси длиной соответственно а, b, с, расположенные взаимно перпендикулярно;
моноклинной системе: две оси (а и с) образуют между собой угол β, а третья ось b расположена под прямым углом к осям а и с;
триклинной системе: три оси а, b и с образуют между собой углы α, β и γ
Между гранями кристалла и осями должны существовать рациональные отношения: отрезки осей, отсекаемых гранью, относятся к длинам осей а, b и с, как простые числа. Схематическое изображение осей кристаллов и граней показано на рисунках 5 и 6.
Рис. 5 Схематическое изображение осей кристаллов и граней
§
Зонке (1879 г.), Чермак, Шенфлис, Федоров (1891 г.) и другие показали геометрически, что все кристаллические формы можно представить как результат распределения точек (мельчайших вещественных частиц) в пространстве по законам симметрии; получающиеся конфигурации они назвали кристаллическими решетками.
Распределяя согласно элементам симметрии точки в пространстве, они получили 230 комбинаций, 230 кристаллических решеток, которые соответствуют всем встречающимся в природе кристаллическим формам.
Последующее исследование кристаллов с помощью лучей Рентгена немецким ученым Лауэ (1912 г.) подтвердило те предположения и выводы, которые были сделаны косвенным путем. Были получены прямые доказательства существования атомов, ионов и способов их расположения в пространстве.

Рис.6 Схематическое изображение осей кристаллов и граней
Кристаллические решетки, как выяснилось, делятся на следующие группы: атомные, ионные, молекулярные и металлические.
Атомные решетки. Каждое узловое место в атомной решетке занято нейтральным атомом. Примером может служить кристаллическая решетка аргона, приведенная на рисунке 7.
Рис. 7. Кристаллическая решетка аргона
Ионные решетки. Каждое узловое место в ионной решетке занято ионом. Примеры ионных решеток приведены на рисунках 8 и 9. На рис. 8, а показана кристаллическая решетка Na Cl—, на рис. 8,6 — решетка CsJ; на рис. 9 приведена кристаллическая решетка CaF2.
Кристаллическая решетка Na Cl— типична для бинарных электролитов, состоит из двух центрированных в гранях решеток, вдвинутых одна в другую на ½ длины ребра куба. Одна решетка — катиона Na , другая такая же—аниона С1—.
Рис. 8. Кристаллическая решетка NaCl и CsJ
Кристаллическая решетка Cs J— представляет собой сочетание двух простых кубических решеток: решетки иона Cs и решетки иона J—, вдвинутых одна в другую так, что в центре куба находится; ион йода, а в углах — ионы Cs . Эта решетка центрирована в пространстве так, что в центре куба находится анион, а в углах —катионы.
Рис. 9. Кристаллическая решетка CaF2
Кристаллическая решетка Ca2 F2— типична для многих тройных электролитов. Здесь ионы Са2 образуют кристаллическую, центрированную в гранях, решетку, ионы же F— расположены в серединах восьми маленьких кубов, на которые может быть разложен большой куб.
В ионных кристаллических решетках отдельные места могут занимать сложные и комплексные ионы. Примеры: решетка нитрата натрия Na NO3— (pис 9, а) и решетка гексахлороплатината калия K [PtCl6]2- (рис. 10,б). Здесь отдельные места занимают ионы: Na , К , NO3—, [PtCl6]2-.
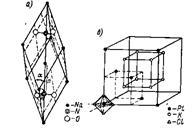
Рис. 10. Кристаллическая решетка нитрата натрия и гексахлороплатината калия.
В кристаллической решетке нитрата натрия каждый ион NO3— занимает одно место, причем в центре тетраэдра — атом азота N 5, а в углах — атомы кислорода О; атомы сближены друг с другом и составляют прочную, крепко стянутую группу.
Такую же группу представляет собой прочный комплексный ион [PtCl6]2- . Пространственно он построен так: в центре октаэдра — ион Pt4 , а в углах — ионы С1—
Ионы [PtCl6]2- занимают углы кубической, центрированной в гранях, кристаллической решетки. Ионы К составляют куб.
Молекулярные решетки. В молекулярных решетках отдельные места занимают молекулы. Примером молекулярных решеток соединений, которые рассматриваются в неорганической химии, могут служить кристаллические решетки окиси алюминия (рис. 11, а) и двуокиси углерода СО2 (рис. 11,6). В кристаллической решетке окиси алюминия Аl2Оз углы ромба с длиной ребра αo = 5,12А занимают близко расположенные друг к другу группы атомов, образующие нейтральную молекулу.
В кристаллической, центрированной в гранях, решетке двуокиси углерода отдельные места занимают нейтральные молекулы СО2, очень сближенные группы из трех атомов С и 2О, сгруппированные так, как это показано на рис. 11.
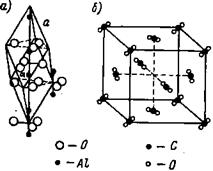
Рис. 11. Кристаллическая решетка окиси алюминия и двуокиси углерода СО2
Металлические решетки. Металлические решетки характеризуются особыми свойствами, отличающими их от других типов кристаллических решеток. В узлах металлических решеток находятся не атомы, а положительные ионы. Внешние электроны атомов металлов свободно мигрируют внутри кристаллической решетки, переходя от одного иона к другому, т. е. ведут себя подобно молекулам газа, поэтому всю совокупность электронов в кристаллической решетке металлов называют электронным газом.
Рис. 12. Кристаллическая решетка металлического натрия
Таким образом, металлическую решетку можно рассматривать как ионную решетку, находящуюся в «атмосфере» электронного газа из внешних электронов. Такова, например, решетка металлического натрия (рис. 12). Характерные свойства металлов — электропроводность и теплопроводность, в частности, зависят от передвижения электронов внутри решетки. Под воздействием внешнего электрического поля валентные электроны, число которых у атомов металлов невелико (1, 2 или 3), перемещаются в направлении поля, создавая электрическую проводимость.
СПЛАВЫ
Для изготовления оборудования в различных отраслях современной промышленности используются самые разнообразные материалы, как природные, так и созданные руками человека. Однако основа современной техники — машины и механизмы — изготовляются в основном из металлических материалов — металлов, сплавов металлов друг с другом и с некоторыми неметаллами, прежде всего с углеродом. Это связано с тем, что из всех видов материалов металлические материалы обладают наиболее ценными механическими свойствами. Кроме того, металлические материалы очень многочисленны и разнообразны по своим свойствам.

Рис. 13 Рис. 14
В жидком состоянии большинство металлов растворяются друг в друге и образуют однородный жидкий сплав. При кристаллизации из расплавленного состояния различные металлы ведут себя по-разному. Основными случаями являются при этом следующие три. . .
1. В твердом состоянии сплавляемые металлы не растворяются и химически не взаимодействуют друг с другом. При этих условиях сплав представляет собою механическую смесь и состоит из кристаллитов одного и другого компонентов, отчетливо выявляемых на микрошлифе (рис. 13)
2. Сплавляемые металлы взаимодействуют друг с другом, образуя химическое соединение.
3. При кристаллизации из расплава растворимость металлов друг в друге сохраняется. Образуются однородные кристаллы.
В этом случае твердая фаза носит название твердого раствора (рис. 14). При этом для одних металлов их взаимная растворимость в твердом состоянии неограниченна, другие же растворимы друг в друге лишь до определенных концентраций.
§
При изучении свойств сплавов очень большое значение имеют диаграммы состояния, характеризующие состояние сплавов различного состава при разных температурах. Такие диаграммы показывают термодинамически устойчивые состояния, т. е. состояния, отвечающие минимуму энергии Гиббса системы. Их называют также разновесными диаграммами, так как они показывают, какие фазы могут сосуществовать при данных условиях.
Диаграммы состояния получают экспериментально. Обычно для этого строят кривые охлаждения и по остановкам и перегибам на них, вызванным тепловыми эффектами превращений, определяют температуры этих превращений. Для получения кривых охлаждения приготовляют из двух металлов изучаемой системы ряд смесей различного состава. Каждую из приготовленных смесей расплавляют. Получающиеся жидкие сплавы (расплавы) медленно охлаждают, отмечая через определенные промежутки времени температуру остывающего сплава. По данным наблюдений строят кривые охлаждения, откладывая на оси абсцисс время, а на оси ординат — температуру (рис. 15).
На рис. 15 слева показано, какой вид имеет кривая охлаждения чистого расплавленного металла. Сначала понижение температуры плавно идет по кривой ak. В точке k происходит перелом кривой, начинается образование твердой фазы (кристаллизация), сопровождающееся выделением теплоты, вследствие чего температура некоторое время остается постоянной (кривая идет параллельно оси абсцисс). Когда вся масса расплавленного металла затвердеет, опять начинается плавное понижение температуры по кривой св.
Рис.15 Кривые охлаждения Рис. 16 Содержание компонента
Иногда остановки в падении температуры наблюдаются и на кривой охлаждения твердого металла, указывая на связанные с выделением теплоты процессы, происходящие уже в твердом веществе, например переход из одной кристаллической формы в другую.
Несколько иной вид имеет кривая охлаждения сплава двух металлов. Такая кривая изображена на рис. 15 справа. Точка к, как и на первой кривой, отвечает началу затвердевания — началу выделения из сплава кристаллов одного из входящих в него металлов. При этом состав, остающегося жидким, сплава изменяется, и температура его затвердевания непрерывно понижается во время кристаллизации. Однако выделяющаяся при кристаллизации теплота все же замедляет ход охлаждения, вследствие чего в точке k происходит перелом кривой. Выпадение кристаллов и плавное понижение температуры происходят до тех пор, пока не достигается температура, при которой сплав закристаллизовывается без изменения состава. Здесь падение температуры приостанавливается точка k1). Когда кристаллизация закончится, температура падает по кривой св.
Имея достаточный набор сплавов, различающихся содержанием компонентов и определив в каждом сплаве температуры превращений, можно построить диаграмму состояния. На диаграммах состояния по вертикальной оси откладывают температуру, а по горизонтальной — состав сплава (концентрацию одного из компонентов). Для сплавов, состоящих из двух компонентов, обозначаемых буквами X и Y, состав характеризуется точкой на отрезке прямой, принятом за 100%. Крайние точки соответствуют индивидуальным компонентам. Любая же точка отрезка, кроме крайних, характеризует состав двойного сплава. На рисунке 16 числа указывают содержание компонента Y. Например, точка К отвечает сплаву, состоящему из 20% Y и 80% X.
Рассмотрим четыре простых случая — четыре типа диаграмм, соответствующие упомянутым выше типам сплавов: механической смеси, твердому раствору с неограниченной и с ограниченной растворимостью и химическому соединению.
Диаграмма состояния для сплавов, образующих механические смеси индивидуальных компонентов. В качестве примера диаграммы этого типа на рис. 147 приведена диаграмма состояния системы Рb—Sb. Точки А и В на диаграмме — это температуры плавления компонентов системы: свинца (327°С) и сурьмы (631°С). В сплавах рассматриваемого типа добавка одного компонента к другому, согласно закону Рауля, понижает температуру начала его кристаллизации (затвердевания). Кривая АЕ показывает температуру кристаллизации свинца из расплавов, богатых свинцом, а кривая BE— температуру кристаллизации сурьмы из расплавов, богатых сурьмой. Видно, что по мере увеличения содержания второго компонента температуры кристаллизации как свинца, так и сурьмы понижаются. Точка Е принадлежит обеим кривым: из расплава, состав которого отвечает этой точке, кристаллизуются одновременно оба металла. Эта совместная кристаллизация происходит при самой низкой температуре. Отвечающий точке Е состав называется эвтектическим составом, а соответствующий сплав — эвтектическим сплавом или просто эвтектикой (от греческого «эвтектикос» — хорошо плавящийся). Для системы Pb—Sb эвтектика состоит из 13% Sb и 87% Рb; она плавится и кристаллизуется при 246°С.
Рассмотрим подробнее процесс «кристаллизации расплава. Пусть это будет расплав, содержащий 40% Sb и 60% Рb (точка k на рис. 17). При охлаждении этого расплава до 395 °С (точка l) из него начнут выпадать кристаллы. Это будут кристаллы избыточного по сравнению с эвтектикой компонента, в данном случае — сурьмы. Теперь сплав стал двухфазным. На диаграмме состояния ему отвечают две точки: точка l (расплав) и точка m(кристаллы сурьмы). Кристаллизация некоторого количества сурьмы изменит состав расплава; он станет беднее сурьмой и, следовательно, богаче свинцом. Точка на диаграмме, отвечающая расплаву, сместится немного влево. Поскольку охлаждение продолжается, эта точка вновь дойдет до кривой — из расплава снова выпадет какое-то количество кристаллов сурьмы. Таким образом, по мере охлаждения и кристаллизации точка, отвечающая расплаву, двигается вниз и влево по кривой кристаллизации сурьмы, а точка, отвечающая кристаллам сурьмы, — вниз по правой вертикальной оси. Когда расплав достигнет эвтектического состава, из него станут выпадать очень мелкие кристаллы обоих компонентов (эвтектика), пока не закристаллизуется все взятое количество вещества. Получившийся сплав будет представлять собою смесь эвтектики с кристаллами сурьмы.
Рис.17 Процесс кристаллизации расплава.
Если исходить из расплава, содержащего небольшой процент сурьмы (меньше эвтектического), то весь процесс будет происходить аналогично рассмотренному, с той разницей, что вначале будут выпадать кристаллы не сурьмы, а свинца. Полученный сплав будет иметь структуру, представляющую собой смесь эвтектики с кристаллами свинца. Наконец, если исходить из расплава эвтектического состава, то весь сплав закристаллизуется при 246 °С и будет представлять собой эвтектику.
Если верхние кривые диаграммы на рис. 18 (АЕ и BE) показывают температуру начала кристаллизации, то нижняя — горизонталь, проходящая через точку Е, — показывает температуру окончания кристаллизации сплава. Как видно, для систем имеющих диаграммы рассматриваемого типа, температура окончания кристаллизации не зависит от состава сплава.
Рис.18. Процесс кристаллизации расплава.
При плавлении твердых сплавов горизонталь, проходящая через точку Е, показывает температуру начала плавления. В рассматриваемом случае эта температура не зависит от состава сплава, потому что плавление начинается с эвтектики, входящей в состав всех сплавов системы (кроме индивидуальных компонентов). При этом температура сплава будет оставаться постоянной, пока вся имеющаяся в нем эвтектика не расплавится. Дальнейшее нагревание приведет к повышению температуры — начнут плавиться кристаллы чистого компонента, которые находились в исходном сплаве в смеси с эвтектикой. Состав расплава будет обогащаться этим компонентом, и точка, отвечающая расплаву, будет двигаться по соответствующей ветви верхней кривой. Когда плавление закончится, т. е. когда твердая фаза исчезнет, тогда состав расплава станет таким же, каким был состав исходного сплава. Таким образом, если исходить из твердого сплава, то горизонталь, проходящая через точку Е, показывает температуру начала, а кривые АЕ и BE — окончания плавления.
Из сказанного ясно, что области I на диаграмме рис. 17 отвечает расплав, областям II и III соответствует сосуществование расплава с кристаллами избыточного компонента, областям IV и V отвечает смесь эвтектики с зернами свинца (область IV) или сурьмы (область V).
Как уже говорилось, по горизонтальной оси диаграмм состояния откладывается состав взятого сплава. Однако для областей, отвечающих равновесию двух фаз, по этой оси можно также устанавливать составы этих фаз. Пусть, например, сплав 5% Sb и 95% Рb нагрет до 270 °С. Такому сплаву отвечает точка а на диаграмме состояния (рис. 17). Проведем через эту точку горизонталь до пересечения с ближайшими линиями диаграммы. Мы получим точки b и с. Они показывают, что взятому сплаву при 270 °С отвечает равновесие кристаллов свинца (точка b) с расплавом, состав которого определяется абсциссой точки с (приблизительно 10% Sb и 90% Рb).
Диаграмма состояния для сплавов с неограниченной растворимостью в твердом состоянии. На рис. 19 приведена диаграмма состояния системы Ag—Аu, представляющая собой простейший пример диаграмм этого типа, Как и в предыдущих случаях, точки А и В показывают температуры плавления компонентов. Вид кривых плавления (нижняя кривая) и затвердевания (верхняя кривая) обусловлен в этом случае — тем, что кристаллы, выделяющиеся при охлаждении расплава, всегда содержат оба компонента (кроме, конечно, кристаллизации чистых серебра или золота).
Рис.19. Диаграмма состояния системы Ag—Аu
Рассмотрим, как происходит кристаллизация расплавов в этом случае. Пусть исходный жидкий сплав соответствует точке d на диаграмме (рис. 19). При охлаждении его до температуры t1 (точка е) начинается кристаллизация. Кристаллы представляют собой твердый раствор, более богатый тугоплавким компонентом— золотом (точка р). Поэтому в ходе кристаллизации жидкая фаза обедняется тугоплавким компонентом, и точка диаграммы, отвечающая расплаву, смещается несколько влево. По мере охлаждения эта точка движется вниз, вновь доходит до кривой и процесс кристаллизации продолжается. Таким образом, охлаждение расплава сопровождается выпадением кристаллов твердого раствора, обогащенных тугоплавким компонентом — золотом, и обогащением расплава легкоплавким компонентом — серебром. Соответствующие точки на диаграмме при этом перемещаются: состав жидкой фазы изменяется по верхней линии, а состав твердого раствора — по нижней. При медленном проведении процесса кристаллизация заканчивается по достижении такой температуры 1% при которой образующиеся кристаллы имеют состав исходного сплава (точка r).
Таким образом, области I на диаграмме состояния рассматриваемой системы (рис. 19) отвечает расплав, области II— сосуществование расплава и кристаллов твердого раствора, области III твердый раствор. При равновесии точки обеих кривых на диаграмме связаны между собой: каждой температуре отвечает расплав определенного состава и кристаллы тоже определенного состава, но другого, чем состав расплава (например, точке е отвечает точка р).
В ходе процесса кристаллизации температура системы понижается и равновесие между расплавом и кристаллами, образовавшимися ранее, т. е. при более высокой температуре, нарушается. Поэтому кристаллизация сопровождается диффузией, в результат чего при медленном проведении процесса зерна всего сплава получаются однородными и имеют одинаковый состав. При быстром охлаждении процессы диффузии не успевают происходить и сплав получается неоднородным. Как и в предыдущем случае, по горизонтальной оси диаграммы можно устанавливать составы равновесных фаз, в данном случае — расплава и находящегося в равновесии с ним твердого раствора. Например, система, которой отвечает точка s, состоит из расплава, состав которого отвечает точке е, и кристаллов состава, соответствующего точке р.
Диаграмма состояния для сплавов с ограниченной взаимной растворимостью в твердом состоянии. В сплавах этого типа, образуемых компонентами X и Y, могут существовать жидкая фаза и два твердых раствора: раствор компонента X в Y и раствор компонента Y в X. В простейшем случае эти два твердых раствора образуют эвтектику; к такому типу принадлежит система Pb—Sn, диаграмма состояния которой приведена на рис. 20. Отметим прежде всего, что области I здесь отвечает расплав, области II — твердый раствор олова в свинце, области III — твердый раствор свинца в олове.
Для того чтобы понять, существованию каких фаз отвечают другие области на диаграмме и кривые на ней, рассмотрим, как протекает в системе данного типа кристаллизация расплавов.
Рис.20. Диаграмма состояния системы Pb—Sn
Сначала будем исходить из жидкого сплава, богатого свинцом (точка d на рис. 20). При охлаждении этого расплава до температуры t1 (точка е) начнется выделение кристаллов твердого раствора олова в свинце. Состав этих кристаллов отвечает точке р; они богаче свинцом, чем исходный расплав, так что при кристаллизации расплав обедняется свинцом. Как и в предыдущих случаях, точки на диаграмме, отвечающие расплаву и образующимся кристаллам, перемещаются: состав жидкой фазы изменяется по линии АЕ, а состав кристаллов — по линии AD. По достижении температуры t2(точка r) образующиеся кристаллы имеют состав исходного сплава. Если процесс проводится достаточно медленно, то при температуре t2 кристаллизация заканчивается, подобно тому, как это происходит в системах с неограниченной взаимной растворимостью (см. выше).
Кривая ADF показывает растворимость олова в твердом свинце при различных температурах. Видно, что растворимость максимальна, при 183,3 °С. Поэтому при охлаждении кристаллов до температуры t3 (точка s) твердый раствор делается насыщенным. В нем начнет протекать превращение в твердом состоянии: кристаллы твердого раствора на основе свинца, состав которых отвечает точке s, будет превращаться в кристаллы твердого раствора на основе олова, состав которых соответствует точке q. При постоянной температуре кристаллы этих двух твердых растворов будут находиться в равновесии. Однако при дальнейшем охлаждение равновесие нарушится и превращение одних кристаллов в другие будет продолжаться. При этом кристаллы твердого раствора на основе свинца будут обедняться оловом — их состав будет изменяться по кривой DF; одновременно по кривой CG будет изменяться состав кристаллов твердого раствора на основе олова.
Теперь рассмотрим охлаждение жидкого сплава, не столь богатого свинцом (точка f). По охлаждении до температуры (точка g) из расплава начнут выделяться кристаллы твердого раствора на основе свинца; их состав отвечает точке h. По мере выделения этих кристаллов, расплав обогащается оловом: его состав изменяется по линии АЕ, а состав выделяющихся кристаллов — по линии AD. Когда точка, отвечающая расплаву, достигает точки Е, — из расплава выделяются кристаллы обоих твердых растворов; при этом состав кристаллов твердого раствора на основе свинца отвечает точке D, а состав кристаллов твердого раствора на основе олова — точке С. Ясно, что точка Е представляет собой эвтектическую точку, а выделяющаяся смесь кристаллов — эвтектическую смесь.
В области температур ниже 183,3 °С растворимость свинца в олове и олова в свинце с понижением температуры уменьшается. Поэтому при дальнейшем охлаждении сплава образовавшиеся кристаллы изменяют свой состав. Состав кристаллов твердого раствора олова в свинце изменяется по кривой DF, а кристаллов твердого раствора свинца в олове — по кривой CG.
Аналогично протекает кристаллизация расплавов, богатых оловом. В этом случае кристаллизация начинается с выделения кристаллов твердого раствора на основе олова.
На основании сказанного можно заключить, что областям IV и V на диаграмме отвечает сосуществование жидкого расплава и кристаллов твердого раствора на основе свинца (область IV) или на основе олова (область V), а областям VI и VII — смеси кристаллов эвтектики с кристаллами твердого раствора на основе свинца (область VI) или твердого раствора на основе олова (область VII).
Металлы образуют друг с другом многочисленные соединения, называемые интерметаллическими. Энтальпии образования подобных соединений обычно невелики; лишь в некоторых случаях (например, при взаимодействии алюминия с расплавленной медью) их образование сопровождается значительным экзотермическим эффектом. Многие металлы образуют по несколько соединений друг с другом, например, AuZn, Au3Zn5, AuZn3; Na4Sn, NaSn, NaSn2.
На рис. 21 приведена диаграмма состояния системы Mg—Pb. Эта система служит простейшим примером систем, в которых образуются химические соединения: свинец образует с магнием только одно соединение Mg2Pb, а в твердом состоянии эти металлы взаимно нерастворимы.
Рис.21. Диаграмма состояния для сплавов, образующих химические соединения.
От рассмотренных ранее диаграмм эта диаграмма отличается наличием максимума на кривой начала кристаллизации. Этот максимум (точка С) отвечает температуре плавления соединения Mg2Pb. Абсцисса точки максимума указывает состав соединения. На диаграмме имеются две эвтектики Е1 и E2 Эвтектика Е1 представляет собой смесь кристаллов Mg и Mg2Pb, а эвтектика Е2 — кристаллов Рb и Mg2Pb.
Таким образом, диаграмма системы с химическим соединением как бы составлена из двух диаграмм первого типа. Если компоненты системы образуют между собой два или более химических соединения, то диаграмма как бы составлена из трех, четырех и более отдельных диаграмм первого типа.
Кристаллизация сплавов в этом и в подобных случаях происходит аналогично кристаллизации сплавов, образующих диаграммы первого типа. Отличие состоит в том, что, кроме выделения кристаллов индивидуальных компонентов, происходит еще образование кристаллов соединения. По линии АЕ1 из расплавов при охлаждении выделяется магний, по линии Е2В — свинец и по линии Е1СЕ2 — Mg2Pb. Так, если охлаждать жидкий сплав, содержащий 40% РЬ (60% Mg), то из него сначала будут выделяться кристаллы магния. Когда температура понизится до 460°С, вся оставшаяся еще жидкой часть сплава начнет затвердевать при этой температуре, образуя эвтектическую смесь мельчайших кристалликов магния и химического соединения Mg2Pb.
При охлаждении жидкого сплава, содержащего 75% РЬ, сначала будут выделяться кристаллы Mg2Pb. Это будет происходить до тех пор, пока температура не снизится до 460 °С — точки образования эвтектики. Аналогичные процессы с выделением эвтектики Е2 (при 250 °С) будут протекать при содержании в сплаве более 80% Рb.
Нетрудно понять, что области I на, рис. 21 отвечает жидкий сплав, областям II—V—равновесия жидкого сплава и соответствующих кристаллов (в области II — кристаллы Mg, в. областях III и IV— кристаллы Mg2Pb, в области V — кристаллы РЬ), а областям VI — IX — твердые сплавы [Mg эвтектика Е1 (VI), Mg2Pb эвтектика Е1 (VII), Mg2Pb эвтектика Е2 (VIII), Pb эвтектика E2 (IX)].
Мы рассмотрели наиболее простые, но в то же время важнейшие типы диаграмм состояния. Для многих систем диаграммы состояния носят значительно более сложный характер. Так, ряд металлов и сплавов испытывают превращения в твердом состоянии, переходя из одной модификации в другую. На диаграмме состояния появляются при этом кривые, разграничивающие области устойчивости этих модификаций.
Существуют методы построения диаграмм состояния тройных систем — систем, состоящих из трех компонентов.
Для технически важных систем диаграммы состояния изучены и приводятся в специальной литературе. Они имеют широкое применение в различных областях науки и техники, служат научной основой при подборе сплавов, обладающих заданными свойствами, при изыскании методов термической обработки сплавов, при разработке и создании новых сплавов. Примером системы, имеющей очень большое практическое значение, может служить система Fe — С.
Нахождение в природе

Накопление O
2
в
атмосфере
Земли. Зелёный график — нижняя оценка уровня кислорода, красный — верхняя оценка.
1
. (3,85—2,45 млрд лет назад) — O
2
не производился
2
. (2,45—1,85 млрд лет назад) — O
2
производился, но поглощался океаном и породами морского дна
3
. (1,85—0,85 млрд лет назад) — O
2
выходит из океана, но расходуется при окислении горных пород на суше и при образовании озонового слоя
4
. (0,85—0,54 млрд лет назад) — все горные породы на суше окислены, начинается накопление O
2
в атмосфере
5
. (0,54 млрд лет назад — по настоящее время) — современный период, содержание O
2
в атмосфере стабилизировалось
Кислород — самый распространённый в земной коре элемент, на его долю (в составе различных соединений, главным образом силикатов) приходится около 47 % массы твёрдой земной коры. Морские и пресные воды содержат огромное количество связанного кислорода — 85,82 % (по массе).
В атмосфере содержание свободного кислорода составляет 20,95 % по объёму и 23,10 % по массе (около 1015 тонн[7]). Однако до появления первых фотосинтезирующих микробов в архее 3,5 млрд лет назад в атмосфере его практически не было.
Свободный кислород в больших количествах начал появляться в палеопротерозое (3—2,3 млрд лет назад) в результате глобального изменения состава атмосферы (кислородной катастрофы). Первый миллиард лет практически весь кислород поглощался растворённым в океанах железом и формировал залежи джеспилита.
Наличие большого количества растворённого и свободного кислорода в океанах и атмосфере привело к вымиранию большинства анаэробных организмов. Тем не менее, клеточное дыхание с помощью кислорода позволило аэробным организмам производить гораздо больше АТФ, чем анаэробным, сделав их доминирующими[10].
С начала кембрия 540 млн лет назад содержание кислорода колебалось от 15 % до 30 % по объёму[11]. К концу каменноугольного периода (около 300 миллионов лет назад) его уровень достиг максимума в 35 % по объёму, который, возможно, способствовал большому размеру насекомых и земноводных в это время[12].
Основная часть кислорода на Земле выделяется фитопланктоном Мирового океана. Около 60 % кислорода от используемого живыми существами расходуется на процессы гниения и разложения, 80 % кислорода, производимого лесами, уходит на гниение и разложение растительности лесов[13].
Деятельность человека очень мало влияет на количество свободного кислорода в атмосфере[14][нет в источнике].
Кислород входит в состав многих органических веществ и присутствует во всех живых клетках. По числу атомов в живых клетках он составляет около 25 %, по массовой доле — около 65 %[6].
В 2022 году датские учёные доказали, что свободный кислород входил в состав атмосферы уже 3,8 млрд лет назад[16].
Химические свойства
Сильный окислитель, самый активный неметалл после фтора, образует бинарные соединения (оксиды) со всеми элементами, кроме гелия, неона, аргона, фтора (с фтором кислород образует фторид кислорода, так как фтор более электроотрицателен, чем кислород).
- 4Li O2⟶2Li2O{displaystyle {ce {4Li O2 -> 2Li2O}}}
- 2Sr O2⟶2SrO{displaystyle {ce {2Sr O2 -> 2SrO}}}
Окисляет соединения, которые содержат элементы с не максимальной степенью окисления:
- 2NO O2⟶2NO2↑{displaystyle {ce {2NO O2 -> 2NO2 ^}}}
Окисляет большинство органических соединений в реакциях горения:
- 2C6H6 15O2⟶12CO2 6H2O{displaystyle {ce {2C6H6 15O2 -> 12CO2 6H2O}}}
- CH3CH2OH 3O2⟶2CO2 3H2O{displaystyle {ce {CH3CH2OH 3O2 -> 2CO2 3H2O}}}
При определённых условиях можно провести мягкое окисление органического соединения:
- CH3CH2OH O2⟶CH3COOH H2O{displaystyle {ce {CH3CH2OH O2 -> CH3COOH H2O}}}
Кислород реагирует непосредственно (при нормальных условиях, при нагревании и/или в присутствии катализаторов) со всеми простыми веществами, кроме Au и инертных газов (He, Ne, Ar, Kr, Xe, Rn); реакции с галогенами происходят под воздействием электрического разряда или ультрафиолета.
Косвенным путём получены оксиды золота и тяжёлых инертных газов (Xe, Rn). Во всех двухэлементных соединениях кислорода с другими элементами кислород играет роль окислителя, кроме соединений со фтором (см. ниже #Фториды кислорода).
Кислород образует пероксиды со степенью окисления атома кислорода, формально равной −1.
- 2Na O2⟶Na2O2{displaystyle {ce {2Na O2 -> Na2O2}}}
- 2BaO O2⟶2BaO2{displaystyle {ce {2BaO O2 -> 2BaO2}}}
- H2 O2⟶H2O2{displaystyle {ce {H2 O2 -> H2O2}}}
- Na2O2 O2⟶2NaO2{displaystyle {ce {Na2O2 O2 -> 2NaO2}}}
- K O2⟶KO2{displaystyle {ce {K O2 -> KO2}}}
- 3KOH 3O3⟶2KO3 KOH⋅H2O 2O2↑{displaystyle {ce {3KOH 3O3 -> 2KO3 KOH * H2O 2O2 ^}}}
- PtF6 O2⟶O2PtF6{displaystyle {ce {PtF6 O2 -> O2PtF6}}}
В этой реакции кислород проявляет восстановительные свойства.













