- В чём разница между понятиями «масса» и «количество»
- Задача 2
- Закон объемных отношений
- Историческая справка
- Как вычислить молекулярную и молярную массы вещества?
- Нахождение химической формулы вещества по данным об исходном веществе и о продуктах его сгорания (по уравнению химической реакции)
- Нахождение химической формулы вещества по массовым долям элементов
- Нахождение химической формулы вещества по массовым долям элементов, если указана плотность или относительная плотность данного вещества в газообразном состоянии
- Относительная плотность газа по кислороду 2. вычислите молярную массу этого газа, назовите этот газ — знания.site
- Относительная плотность одного газа по другому
- Пример 2
- Решение задач на плотность и молярный объём газов
- Способы вычисления средней молярной массы газовой смеси
- Формула для вычисления массы через объем и плотность
В чём разница между понятиями «масса» и «количество»
Если мы будем производить подобные расчеты, соответствующие этому заданию, для простых веществ, образованных различными элементами, то всякий раз получим одно и то же число — 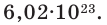
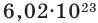
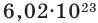
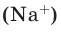
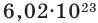
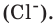
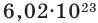 постоянной Авогадро (Na). Постоянная Авогадро отличается от числа Авогадро тем, что измеряется определенной единицей
постоянной Авогадро (Na). Постоянная Авогадро отличается от числа Авогадро тем, что измеряется определенной единицей 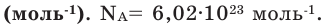
Количество вещества можно вычислить по следующей формуле:
Здесь 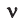
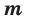 М — молярная масса, N — заданное количество молекул,
М — молярная масса, N — заданное количество молекул, 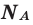
Задача 2
Какой объем займет водород в количестве 0,7 моль?
Дано:
моль.
Решение:
По формуле мы можем найти объем .
Зная, что молярный объем при обычных условиях составляет 22,4 л/моль, вычислим фактический объем водорода:
Ответ: объем водорода составляет 15,68 литров.
Закон объемных отношений
В химических реакциях соотношение объемов, вступающих в реакцию, и полученных газов равно соотношению их коэффициентов. Например:
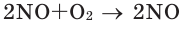
Численное соотношение объемов, молей и молекул газов равно друг другу.
Можно производить следующие вычисления по смесям:
3) Массовое соотношение двух газов: 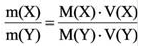
Историческая справка
В 1811 году химик Амедео Авогадро предположил, что если взять два равных объема газов в равных значимых условиях (при одинаковой температуре и давлении), то количество молекул в этих объемах тоже будет одинаковым. Опираясь на свою гипотезу, он определил атомные и молекулярные массы многих веществ, а также рассчитал количество атомов в молекулах воды, оксидов азота и т. д. Однако в научных кругах гипотеза Авогадро долго не находила понимания. Общепринятой она стала только в 1860 году.
Как вычислить молекулярную и молярную массы вещества?
Для этого нужно сложить массы всех атомов в этой молекуле.
Пример 1. В молекуле воды Н2О 2 атома водорода и 1 атом кислорода. Атомная масса водорода = 1, а кислорода = 16. Поэтому молекулярная масса воды равна 1 1 16 = 18 атомных единиц массы, а молярная масса воды =18 г/моль.
Пример 2. В молекуле серной кислоты Н2SO4 2 атома водорода, 1 атом серы и 4 атома кислорода. Поэтому молекулярная масса этого вещества составит 1 2 32 4 16 = 98 а.е.м, а молярная масса — 98 г/моль.
Пример 3. В молекуле сульфата алюминия Al2(SO4)3 2 атома алюминия, 3 атома серы и 12 атомов кислорода. Молекулярная масса этого вещества равна 27 · 2 32 · 3 16 · 12 = 342 а.е.м., а молярная масса — 342г/моль.
Нахождение химической формулы вещества по данным об исходном веществе и о продуктах его сгорания (по уравнению химической реакции)
Задача 3. Найдите молекулярную формулу углеводорода, имеющего плотность $1.97$ г/л, если при сгорании $4.4$ г его в кислороде образуется $6.72$ л оксида углерода (IV) (н. у.) и $7.2$ г воды.
Дано:
$m(C_xH_y)=4.4$ г
$ρ(C_xH_y)=1.97$ г/л
$V(CO_2)=6.72$ л
$m(H_2O)=7.2$ г
$C_xH_y-?$
Решение:
1. Напишем схему уравнения горения углеводорода
${C_xH_y}↖{4.4г} O_2→{CO_2}↖{6.72л} {H_2O}↖{7.2г}$
2. Вычисляем молярную массу $C_xH_y·M=ρ·V_m$,
$M=1.97$ г/л$·22.4$ л/моль$=44$ г/моль.
Относительная молекулярная масса $M_r=44$.
3. Определяем количество вещества:
$ν(C_xH_y)={m}/{M}$ или $ν(C_xH_y)={4.4}/{44}=0.1$ моль.
4. Используя величину молярного объема, находим:
$ν(CO_2)={m}/{M}$ или $ν(H_2O)={7.2}/{18}=0.4$ моль.
6. Следовательно: $ν(C_xH_y) : ν(CO_2) : νH_2O=0.1$ моль $: 0.3$ моль $: 0.4$ моль или $1 : 3 : 4$, что должно соответствовать коэффициентам в уравнении и позволяет установить число атомов углерода и водорода:
$C_xH_y O_2→3CO 4H_2O$.
Окончательный вид уравнения:
$C_3H_8 5O_2→3CO_2 4H_2O$.
Ответ: формула углеводорода $C_3H_8$ — пропан.
Нахождение химической формулы вещества по массовым долям элементов
Массовая доля элемента — это отношение его массы к общей массе вещества, в состав которого он входит:
$W={m(эл-та)}/{m(в-ва)}$
Массовая доля элемента ($W$) выражается в долях единицы или в процентах.
Задача 1. Элементарный состав вещества следующий: массовая доля железа $72.41%$, массовая доля кислорода $27.59%$. Выведите химическую формулу.
Дано:
$W(Fe)=72.41%=0.7241$
$W(O)=27.59%=0.2759$
$Fe_{x}O_{y}-?$
Решение:
1. Для расчетов выбираем массу оксида $m$(оксида)$=100$ г. Тогда массы железа и кислорода будут следующими:
$m(Fe)=m_{оксида}·W(Fe); m(Fe)=100·0.7241=72.41$ г.
$m(O)=m_{оксида}·W(O); m(O)=100·0.2759=27.59$ г.
2. Количества вещества железа и кислорода равны соответственно:
$ν(Fe)={m(Fe)}/{M(Fe)};ν(Fe)={72.41}/{56}=1.29.$
$ν(O)={m(O)}/{M(O)};ν(O)={27.59}/{16}=1.72.$
3. Находим соотношение количества веществ железа и кислорода:
$ν(Fe) : ν(O)=1.29 : 1.72.$
Меньшее число принимаем за $1 (1.29=1)$ и находим:
$Fe : O=1 : 1.33$.
4. Так как в формуле должно быть целое число атомов, то это отношение приводим к целым числам:
$Fe : O=1 : 1.33=2 : 2.66=3·3.99=3 : 4$.
5. Подставляем найденные числа и получаем формулу оксида:
$Fe : O=3 : 4$, т. е. формула вещества $Fe_3O_4$.
Ответ: $Fe_3O_4$.
Нахождение химической формулы вещества по массовым долям элементов, если указана плотность или относительная плотность данного вещества в газообразном состоянии
Задача 2. Массовая доля углерода в углеводороде составляет $80 %$. Относительная плотность углеводорода по водороду составляет $15$.
Дано:
$W(C)=80 %$
$D(H_2)=15%$
$C_{x}H_{y}-?$
Решение:
1. Обозначим формулу вещества $C_{x}H_{y}$.
2. Найдем число молей атомов углерода и водорода в $100$ г данного соединения:
$x=n(C); y=ν(H).$
$ν(C)={m(C)}/{M(C)}={80}/{12}=6.6;ν(H)={m(H)}/{M(H)}={20}/{1}=20.$
1 способ.
3. Отношение между атомами:
$x : y=6.6 : 20=1 : 3$, или $2 : 6$.
Простейшая формула вещества $CH_3$.
4. Определяем молекулярную массу углеводорода по относительной плотности ее паров.
$M_r$(вещества)$=2D(H_2)=32D(O_2)=29D$(воздуха).
$M_x=2D(H_2)=2·15=30$ г/моль.
5. Вычисляем относительную молекулярную массу углеводорода по простейшей формуле:
$M_r(CH_3)=A_г(C) 3A_г(H)=12 3=15$.
6. Значения $M_x$ и $M_r$ не совпадают, $M_r={1}/{2}M_x$, следовательно, формула углеводорода $C_2H_6$.
Проверяем: $M_r(C_2H_6)=2A_r(C) 6A_r(H)=2·12 6·1=30$.
Ответ: молекулярная формула углеводорода $C_2H_6$ — этан.
2 способ.
3. Отношение между атомами:
${x}/{y}={6.6}/{20};{x}/{y}={1}/{3.03};y=3.03x.$
4. $M_x=15$.
5. Молярная масса может быть представлена в виде:
$M_r(C_xH_y)=A_r(C)_x A_r(H)_y; M_r(C_xH_y)=12x y$ или $30=12x 1y$.
6. Решаем систему двух уравнений с двумя неизвестными:
${table y=3.03x; 12x y=30;$ $12x 3.03x=30;x=2;y=6.$
Ответ: формула $C_2H_6$ — этан.
Относительная плотность газа по кислороду 2. вычислите молярную массу этого газа, назовите этот газ — знания.site
Дано:
ДО2(газа)=2
Найти:
Mr(газа) — ?
Решение:
1)Вычисления будут идти по формуле: ДО2 = Mr(газа) : М(О2)
2)Найдем молекулярную массу кислорода
М(О2) = 16 х 2 = 32 г/моль
3)Подставим значения
Mr(газа) = ДО2 х М(О2)
Mr(газа) = 2 х 32 = 64 г/моль
Ответ:Mr(газа) = 64 г/моль
Относительная плотность одного газа по другому
Иногда для решения задачи нужно знать, как найти молярную массу газа, о котором сообщается лишь его плотность по воздуху или по другому газу. Это возможно, если знать формулу относительной плотности, которая обозначается буквой D.
, где и — некие газы.
Пример 2
Как посчитать молярную массу газа х, о котором известно, что он в 10 раз плотнее углекислого газа CO2?
Подсчитаем для начала молярную массу углекислого газа:
M(CO2) = Mr(CO2) = 12 2 · 16 = 44.
Ориентируясь на формулу относительной плотности, произведем расчет молярной массы искомого газа х.
М(х) = D(х/CO2) · M(CO2) = 10 · 44 = 440 г/моль.
Ответ: у данного газа молярная масса 440 г/моль.
Решение задач на плотность и молярный объём газов
Теоретический материал смотри на странице «Молярный объём газа«.
Основные формулы и понятния:
| Закон Авогадро При одинаковой температуре и давлении одинаковые объемы любых газов содержат одинаковое кол-во молекул Если V1=V2; T1=T2; P1=P2, то N1=N2 |
Из закона Авогадро, например, следует, что при одинаковых условиях в 1 литре водорода и в 1 литре кислорода содержится одинаковое кол-во молекул, хотя их размеры сильно разнятся.
Первое следствие из закона Авогадро:
| При одинаковых условиях 1 моль любого газа занимает один и тот же объём Если N1=N2; T1=T2; P1=P2, то V1=V2 |
Объём, который занимает 1 моль любого газа при нормальных условиях (н.у.), равен 22,4 литра и называется молярным объёмом газа (Vm).
Vm=V/ν (м3/моль)
Что называют нормальными условиями (н.у.):
- нормальная температура = 0°C или 273 К;
- нормальное давление = 1 атм или 760 мм рт.ст. или 101,3 кПа
Из первого следствия закона Авогадро вытекает, что, например, 1 моль водорода (2 г) и 1 моль кислорода (32 г) занимают один и тот же объем, равный 22,4 литра при н.у.
Зная Vm, можно найти объем любого кол-ва (ν) и любой массы (m) газа:
V=Vm·ν V=Vm·(m/M)
Типовая задача 1: Какой объём при н.у. занимает 10 моль газа?
V=Vm·ν=22,4·10=224 (л/моль)
Типовая задача 2: Какой объём при н.у. занимает 16 г кислорода?
V(O2)=Vm·(m/M) Mr(O2)=32; M(O2)=32 г/моль V(O2)=22,4·(16/32)=11,2 л
Второе следствие из закона Авогадро:
| Относительная плотность одного газа по другому газу равна отношению их молярных или относительных молекулярных масс DY(X) = M(X)/M(Y) = Mr(X)/MrY |
Зная пллотность газа (ρ=m/V) при н.у., можно вычислить молярную массу этого газа: M=22,4·ρ
Плотностью (D) одного газа по другому называют отношение массы определённого объёма первого газа к массе аналогичного объёма второго газа, взятого при одинаковых условиях.
Типовая задача 3: Определить относительную плотность углекислого газа по водороду и воздуху.
Dводород(CO2) = Mr(CO2)/Mr(H2) = 44/2 = 22 Dвоздух = 44/29 = 1,5
| Закон объёмных отношений при одинаковых условиях отношение объёмов газов (а также объёмы газообразных продуктов), которые вступают в реакцию, соотносятся, как небольшие целые числа, коэффициенты в уравнениях реакций показывают числа объёмов реагировавших и образовавшихся газов |
- один объём водорода и один объём хлора дают два объёма хлористого водорода: H2 Cl2=2HCl
- два объёма водорода и один объём кислорода дают два объёма водяного пара: 2H2 O2=2H2O
Задача 1. Сколько молей и молекул содержится в 44 г углекислого газа.
Решение:
M(CO2)=12 16·2=44 г/моль ν = m/M = 44/44 = 1 моль N(CO2) = ν·NA = 1·6,02·1023 = 6,02·1023
Задача 2. Вычислить массу одной молекулы озона и атома аргона.
Решение:
M(O3) = 16·3 = 48 г m(O3) = M(O3)/NA = 48/(6,02·1023) = 7,97·10-23г M(Ar) = 40 г m(Ar) = M(Ar)/NA = 40/(6,02·1023) = 6,65·10-23г
Задача 3. Какой объём при н.у. занимает 2 моля метана.
Решение:
ν = V/22,4 V(CH4) = ν·22,4 = 2·22,4 = 44,8 л
Задача 4. Определить плотность и относительную плотность оксида углерода (IV) по водороду, метану и воздуху.
Решение:
Mr(CO2)=12 16·2=44; M(CO2)=44 г/моль Mr(CH4)=12 1·4=16; M(CH4)=16 г/моль Mr(H2)=1·2=2; M(H2)=2 г/моль Mr(воздуха)=29; М(воздуха)=29 г/моль ρ=m/V ρ(CO2)=44/22,4=1,96 г/моль D(CH4)=M(CO2)/M(CH4)=44/16=2,75 D(H2)=M(CO2)/M(H2)=44/2=22 D(воздуха)=M(CO2)/M(воздуха)=44/24=1,52
Задача 5. Определить массу газовой смеси, в которую входят 2,8 кубометров метана и 1,12 кубометров оксида углерода.
Решение:
Mr(CO2)=12 16·2=44; M(CO2)=44 г/моль Mr(CH4)=12 1·4=16; M(CH4)=16 г/моль 22,4 кубометра CH4 = 16 кг 2,8 кубометра CH4 = x m(CH4)=x=2,8·16/22,4=2 кг 22,4 кубометра CO2 = 28 кг 1,12 кубометра CO2 = x m(CO2)=x=1,12·28/22,4=1,4 кг m(CH4) m(CO2)=2 1,4=3,4 кг
Задача 6. Определить объёмы кислорода и воздуха требуемые для сжигания 112 кубометров двухвалентного оксида углерода при содержании в нем негорючих примесей в объёмных долях 0,50.
Решение:
- определяем объём чистого CO в смеси:
V(CO)=112·0,5=66 кубометров
- определяем объём кислорода, необходимый для сжигания 66 кубов CO:
2CO O2=2CO2 2моль 1моль 66м3 X м3 V(CO)=2·22,4 = 44,8 м3 V(O2)=22,4 м3 66/44,8 = X/22,4 X = 66·22,4/44,8 = 33 м3 или 2V(CO)/V(O2) = V0(CO)/V0(O2) V - молярные объемы V0 - вычисляемые объемы V0(O2) = V(O2)·(V0(CO)/2V(CO))
Задача 7. Как изменится давление в сосуде, заполненном газами водорода и хлора после того, как они вступят в реакцию? Аналогично для водорода и кислорода?
Решение:
- H2 Cl2=2HCl — в результате взаимодействия 1 моля водорода и 1 моля хлора получается 2 моля хлороводорода: 1(моль) 1(моль)=2(моль), следовательно, давление не изменится, поскольку получившийся объм газовой смеси равен сумме объемов компонентов, вступивших в реакцию.
- 2H2 O2=2H2O — 2(моль) 1(моль)=2(моль) — давление в сосуде уменьшится в полтора раза, поскольку из 3 объёмов компонентов, вступивших в реакцию, получилось 2 объёма газовой смеси.
Задача 8. 12 литров газовой смеси из аммиака и четырехвалентного оксида углерода при н.у. имеют массу 18 г. Сколько в смеси каждого из газов?
Решение:
V(NH3)=x л V(CO2)=y л M(NH3)=14 1·3=17 г/моль M(CO2)=12 16·2=44 г/моль m(NH3)=x/(22,4·17) г m(CO2)=y/(22,4·44) г Система уравнений объем смеси: x y=12 масса смеси: x/(22,4·17) y/(22,4·44)=18 После решения получим: x=4,62 л y=7,38 л
Задача 9. Какое кол-во воды получится в результате реакции 2 г водорода и 24 г кислорода.
Решение:
2H2 O2=2H2O
Из уравнения реакции видно, что кол-ва реагирующих веществ не соответствуют отношению стехиометрических коэффициентов в уравнении. В таких случаях вычисления проводят по веществу, которого меньше, т.е., это вещество закончится первым в ходе реакции. Чтобы определить какой из компонентов находится в недостатке, надо обратить внимание на коэффициенте в уравнении реакции.
Количества исходных компонентов ν(H2)=4/2=2 (моль) ν(O2)=48/32=1,5 (моль)
Однако, торопиться не надо. В нашем случае для реакции с 1,5 моль кислорода необходимо 3 моль водорода (1,5·2), а у нас его только 2 моль, т.е., не хватает 1 моль водорода, чтобы прореагировали все полтора моля кислорода. Поэтому, расчёт кол-ва воды будем вести по водороду:
ν(H2O)=ν(H2)=2 моль m(H2O) = 2·18=36 г
Задача 10. При температуре 400 К и давлении 3 атмосферы газ занимает объём 1 литр. Какой объем будет занимать этот газ при н.у.?
Решение:
Из уравнения Клапейрона:
P·V/T = Pн·Vн/Tн Vн = (PVTн)/(PнT) Vн = (3·1·273)/(1·400) = 2,05 л
Способы вычисления средней молярной массы газовой смеси
Здесь: 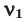
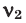
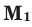
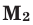

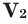
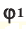
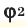
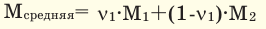 При смешивании газов с одинаковыми молярными массами, которые при одинаковом давлении не вступают друг с другом в реакцию, плотность газовой смеси (при н.у.), а также их средняя молярная масса остаются неизменными. Например, при смешивании
При смешивании газов с одинаковыми молярными массами, которые при одинаковом давлении не вступают друг с другом в реакцию, плотность газовой смеси (при н.у.), а также их средняя молярная масса остаются неизменными. Например, при смешивании 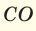 и
и 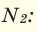 При смешивании газов с различными молярными массами, при одинаковом давлении, средняя молярная масса (при н.у.) и плотность полученной газовой смеси приобретают значение между молярными массами и плотностями смешиваемых газов. Например, при смешивании
При смешивании газов с различными молярными массами, при одинаковом давлении, средняя молярная масса (при н.у.) и плотность полученной газовой смеси приобретают значение между молярными массами и плотностями смешиваемых газов. Например, при смешивании 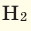 и
и 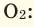
При добавлении газа с большей молярной массой в тот или иной газ при постоянном давлении плотность газовой смеси увеличивается, а при добавлении газа с меньшей молярной массой — уменьшается.
Формула для вычисления массы через объем и плотность
Это количество можно определять по-разному. Если речь идет о числе частиц, то говорят о плотности частиц. Эту величину обозначают буквой n. В СИ она измеряется в м-3. Если имеется ввиду масса вещества, то вводят плотность массы.
= m×n,
где m – масса одной частицы.
Плотность массы можно вычислить по формуле:
= m / V.
Данное выражение можно преобразовать так, чтобы получилась формула массы через объем и плотность:
m = ×V.
Таблица 1. Плотности некоторых веществ.
Вещество | Плотность, кг/м3 | Вещество | Плотность, кг/м3 |
Вещества атомного ядра | 1017 | Вода | 1,00×103 |
Сжатые газы в центре самых плотных звезд | 108 | Жидкий водород | 0,07×103 |
Золото | 1,93×104 | Воздух у поверхности Земли | 1,2 |
Ртуть | 1,36×104 | Воздух на высоте 20 км | 9×10-2 |
Сжатое железо в ядре Земли | 1,2×104 | Наивысший искусственный вакуум | 10-13 |
Сталь | (7,6 – 7,8)×103 | Газы межзвездного пространства | 10-20 |
Алмаз | 3,53×103 | Газы межгалактического пространства | 10-26 |
Алюминий | 2,7 ×103 | ||
Человеческое тело | 1,07 ×103 |
Независимо от степени сжатия плотности жидких и твердых тел лежат в весьма узком интервале значений (табл. 1). Плотности же газов варьируются в весьма широких пределах. Причина заключается в том, что как в твердых телах, так и в жидкостях частицы вплотную примыкают друг к другу.
В этих средах расстояние между соседними частицами составляет величину порядка 1 А и сравнимо с размерами атомов и молекул. По этой причине твердые и жидкие тела обладают очень малой сжимаемостью, чем обусловлено малое различие в их плотности. В газах положение иное.
Среднее расстояние между частицами значительно превышает их размеры. Например, для воздуха у поверхности Земли оно составляет 102 А. Вследствие этого газы обладают большой сжимаемостью, а их плотность может изменяться в очень широких пределах.

