- Введение
- Вычисление относительной плотности газа по другому газу
- Газовые законы
- Идеальный газ
- Как вычислять относительную плотность вещества
- Комбинированный закон
- Математическая модель определения плотности газа
- Плотность газов
- Приведение плотности газа к нормальным, стандартным условиям
- Пример использования калькулятора
- Примеры задач на уравнение менделеева-клапейрона
- Программа python для фильтрации по каналам температуры и давления, и получение результатов
- Реализация измерительного канала давления и температуры
- Решение задач на плотность и молярный объём газов
- Таблица. относительные плотности газов по воздуху по возрастанию в т.ч. горючих и опасных плотности газов, химические формулы газов и молекулярные веса. — инженерный справочник / технический справочник дпва / таблицы для инженеров (ex dpva-info)
- Уравнение клапейрона-менделеева. связь между числом молей газа, его температурой, объемом и давлением.
- Заключение
- Выводы
Введение
Задача измерения параметров газовой смеси широко распространена в промышленности и торговле. Проблема получения достоверной информации при измерении параметров состояния газовой среды и её характеристик с помощью технических средств разрешается принятыми в стандартах методиками выполнения измерений (МВИ), например, при измерении расхода и количества газов с помощью стандартных сужающих устройств [1], или с помощью турбинных, ротационных и вихревых расходомеров и счётчиков [2].
Периодический газовый анализ позволяет установить соответствие между реальной анализируемой смесью и её моделью, по которой в МВИ учитываются физико-химические параметры газа: состав газовой смеси и плотность газа при стандартных условиях. Также в МВИ учитываются теплофизические характеристики газа: плотность при рабочих условиях (давление и температура газа, при которых выполняют измерение его расхода или объёма), вязкость, фактор и коэффициент сжимаемости.
К измеряемым в реальном режиме времени параметрам состояния газа относятся: давление (перепад давлений), температура, плотность. Для измерения этих параметров применяются соответственно средства измерительной техники: манометры (дифманометры), термометры, плотномеры.
Измерение плотности газовой среды допускается измерять прямым или косвенным методами измерения. Результаты как прямых, так и косвенных методов измерения зависят от погрешности средств измерения и методической погрешности. В рабочих условиях, сигналы измерительной информации могут быть подвержены влиянию значительного шума, среднее квадратичное отклонение которого может превышать инструментальную погрешность. В этом случае, актуальной задачей является эффективная фильтрация сигналов измерительной информации.
В данной статье рассматривается методика косвенного измерения плотности газа при рабочих и стандартных условиях c применением фильтра Калмана.
Вычисление относительной плотности газа по другому газу
Решение
1. Найдем относительные молекулярные массы газов, о которых говорится в условии задачи и запишем их в дано.
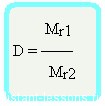
2. Относительная плотность газа X по газу Y равна отношению относительной молекулярной массы X к относительной молекулярной массе Y.
Вычислим это отношение:
DH2(О2) = 32 / 2 = 16
Dвозд(О2) = 32 / 29 = 1,103
3. Запишем ответ
Ответ: DH2(О2) = 16;
Dвозд(О2) = 1,103
Газовые законы
Любое газообразное вещество характеризуется тремя простыми параметрами: объемом, давлением и температурой. Газ тем и хорош, что он заполняет весь предоставленный объем или может сжиматься до минимальных объемов, иногда переходя в состояние жидкости. Сжимать газ можно двумя способами:
- при постоянном давлении уменьшить температуру;
- при постоянной температуре увеличить давление.
Эти две простые формулировки отражают в себе два известных газовых закона: изобару и изотерму. В изобарном процессе изменение температуры приводит к прямо пропорциональному изменению объема. Вспомните жидкий азот: он занимает минимум места, при этом его температура составляет 63,29 К, что соответствует –209 градусам Цельсия.
Если температуру азота поднять до 20 градусов Цельсия, то 1 литр жидкого азота превратится в 700 литров газа. Увеличивается температура, увеличивается объем и наоборот. Эти изменения обусловлены тем, что соотношение объема к температуре газа остается статичным.
В изотермическом процессе температура не изменяется и для сжатия газа придется увеличить давление. Это процесс проще для понимания, так как сдавливая газ мы уменьшаем его объем подобно тому, как утрамбовывание грунта или снега позволяет уложить их более плотно и с меньшим объемом.
Если же объем газа не изменяется, то процесс называется изохорным и в этом процессе отображается взаимосвязь давления и температуры. Согласно закону, изменение одного параметра вызывает прямо пропорциональное изменение другого. Это означает, что увеличение давления в сосуде вызывает рост температуры находящегося там газа. Верно и обратное утверждение.
Идеальный газ
Идеальный газ — это математическая модель с определенными допущениями, которая позволяет исследовать свойства газообразных веществ с достаточной точностью. К допущениям, которые используются в модели идеального газа, относятся:
- пренебрежение размерами молекул;
- силы молекулярного взаимодействия не учитываются;
- соударение атомов и молекул абсолютно упруго;
- газ находится в термодинамическом равновесии.
Благодаря этим допущениям ученые изучили основные свойства газообразных веществ и вывели основные законы, которым подчиняются любые газы. Комбинированный закон объединяет все перечисленные ниже зависимости.
Как вычислять относительную плотность вещества
Такая характеристика, как относительная плотность вещества, показывает, во сколько раз оно тяжелее или легче другого соединения. Этот параметр можно определять по отношению к любому газообразному веществу. В большинстве случаев проводятся расчеты относительно воздуха или водорода. Однако могут попадаться задания, в которых необходимо вычислить относительную плотность и по другим газам, таким как кислород, аммиак или сероводород. В любом случае принцип решения задания един.
Инструкция
Комбинированный закон
Все перечисленные законы подчиняются общей формулировке: при постоянстве одного параметра, отношение двух других также постоянно. Обобщая эти законы в динамике получаем комбинированный газовый закон, который описывается формулой:
где P1, V1 и T1 — соответственно начальные давление, объем и температура, а P2, V2 и T2 — конечные.
Используя данную формулу легко определить динамику параметров во время нагрева газа или его сжатия.
Наша программа позволяет рассчитать соотношение параметров идеального газа при их изменении. Для использования калькулятора требуется задать пять известных величин, после чего программа определит последнее неизвестное. Рассмотрим небольшой пример.
Математическая модель определения плотности газа
Обратимся к классике и вспомним уравнение состояния идеального газа [3]. Имеем:
1. Уравнение Менделеева-Клапейрона:
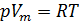


R — универсальная газовая постоянная,
T — абсолютная температура, T=273.16 К.
2. Два измеряемых параметра:
p – давление газа, Па t – температура газа, °С.
Известно, что молярный объём  V и количества молей газа
V и количества молей газа 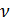
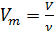
Также известно, что
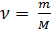
где: m – масса газа, M – молярная масса газа.
Учитывая (2) и (3) перепишем (1) в виде:
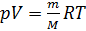
Как известно, плотность вещества

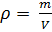
Из (4) и (5) выведем уравнение для плотности газа
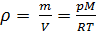
и введём обозначение параметра
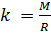
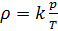
Если состав газовой смеси не меняется, то параметр k является константой. Итак, для расчёта плотности газа необходимо рассчитать молярную массу газовой смеси.
Молярную массу смеси веществ определяем, как среднее арифметическое взвешенное молярной массы массовых долей, входящих в смесь индивидуальных веществ.
Примем известным состав веществ в газовой смеси – в воздухе, который состоит из:
Молярные массы этих веществ воздуха будут соответственно равны:
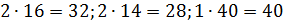
Вычисляем молярную массу воздуха, как среднее арифметическое взвешенное:
Теперь, зная значение константы
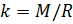
 t:
t:
Плотность газов
Газы в отличие от жидкостей характеризуются малой плотностью. Нормальной плотностью газа называется масса одного его литра при 0°С и давлении 1 кгс/см2. Масса одной молекулы любого газа пропорциональна его плотности.
Плотность газа с изменяется пропорционально давлению и измеряется отношением массы газа m к занимаемому им объему V:

Для практических целей различные газы удобно характеризовать по их плотности относительно воздуха при одинаковых условиях давления и температуры. Поскольку молекулы разных газов имеют различную массу, их плотности при одинаковом давлении пропорциональны молярным массам.
Плотность газов и отношение их плотности к плотности воздуха:
Газ | Химический символ | Молярная масса М, г/моль | Плотность с, кг/м3 | Плотность по отношению к воздуху |
Азот | N2 | 28,016 | l,251 | 0,967 |
Аммиак | NH3 | 17,032 | 0,711 | 0,597 |
Аргон | Аr | 39,944 | 1,784 | 1,380 |
Водород | Н2 | 2,016 | 0,090 | 0,070 |
Воздух | — | 28,98 | 1,293 | 1,000 |
Гелий | Не | 4,003 | 0,178 | 0,138 |
Кислород | 32,00 | 1,429 | 1,105 | |
Криптон | Кr | 83,7 | 3,739 | 2,868 |
Неон | Ne | 20,183 | 0,900 | 0,696 |
Окись углерода | СО | 28,010 | 1,250 | 0,967 |
Углекислый газ | СО2 | 44,010 | 1,977 | 1,529 |
Приведение плотности газа к нормальным, стандартным условиям
Практически, измерения свойств газов проводят в различных физических условиях, и для обеспечения сопоставления между различными наборами данных должны быть установлены стандартные наборы условий [4].
Стандартные условия для температуры и давления – это установленные стандартом физические условия, с которыми соотносят свойства веществ, зависящие от этих условий.
Различные организации устанавливают свои стандартные условия, например: Международный союз чистой и прикладной химии (IUPAC), установил в области химии определение стандартной температуры и давления (STP): температура 0 °C (273.15 K), абсолютное давление 1 бар ( Па);
Национальный институт стандартов и технологий (NIST) устанавливает температуру 20 °C (293,15 K) и абсолютное давление 1 атм (101.325 кПа), и этот стандарт называют нормальной температурой и давлением (NTP); Международная организация по стандартизации (ISO) устанавливает стандартные условия для природного газа (ISO 13443: 1996, подтверждённый в 2022 году): температура 15.00 °С и абсолютное давление 101.325 кПа.
Поэтому, в промышленности и торговле необходимо указывать стандартные условия для температуры и давления, относительно которых и проводить необходимые расчёты.
Плотность воздуха мы рассчитываем по уравнению (8) в рабочих условиях температуры и давления. В соответствии с (6) запишем уравнение для плотности воздуха в стандартных условиях: температура 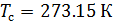
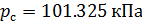
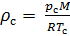
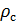
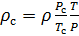
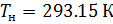

 T и P из уравнения (8), полученные в рабочих условиях.
T и P из уравнения (8), полученные в рабочих условиях.
Пример использования калькулятора
Представим баллон газа объемом 15 л под давлением 120 кПа и при температуре –20 градусов Цельсия. Определим температуру газа, если баллон будет заменен на емкость объемом 10 л и давлением 150 кПа. На первый взгляд у нас есть все параметры, однако в газовых законах температура обязательно указывается в кельвинах, а не градусах.
Для перевода температуры в систему Си достаточно прибавить к значению величину 273. Получаем, что температура газа составляет 253 К. Теперь вводим данные в соответствующие ячейки и смотрим на результат: конечная температура теперь равна 210 К или –63 градуса Цельсия. Очевидно, что газ подчинился приведенным выше законам и при уменьшении объема его температура также уменьшилась.
Примеры задач на уравнение менделеева-клапейрона
В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия . Вопрос: сколько молей кислорода содержится в колбе?
Вопрос: Каков объем этого газа при нормальных условиях? (Напомню, что нормальными условиями для газов считается давление в 1 атмосферу и температура 0 градусов Цельсия)
В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.
Программа python для фильтрации по каналам температуры и давления, и получение результатов
Программа Python методики определения плотности газа по результатам измерений давления и температуры представлена на листинге 2. Информация из измерительной системы выводится в реальном режиме времени.
Результаты расчёта представлены листингом и рис. 4, 5, 6.
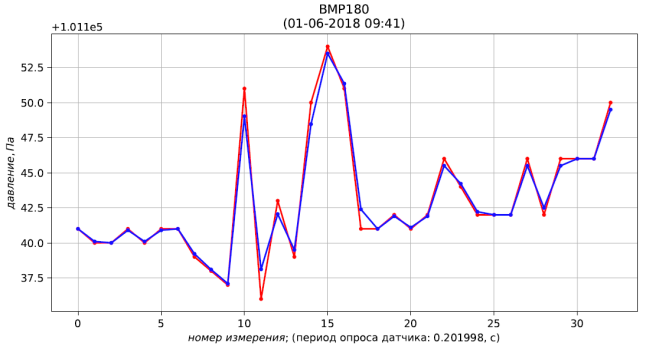
Рис. 4 – результаты измерения (красный) и фильтрации (синий) давления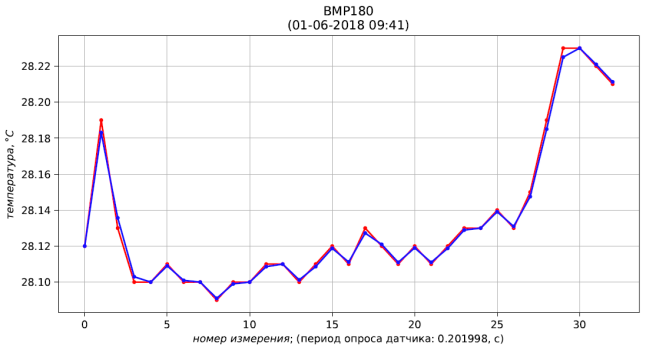
Рис. 5 – результаты измерения (красный) и фильтрации (синий) температуры 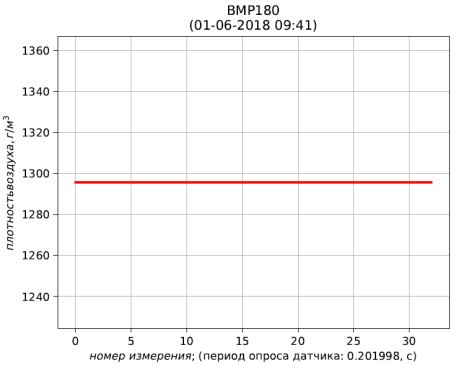
Рис. 6 – результаты расчёта плотности воздуха, приведенной к стандартным условиям (температура 273.15 К; абсолютное давление 101.325 кПа)
Реализация измерительного канала давления и температуры
Для решения многих задач получения информации, в зависимости от их сложности, удобно создавать прототип будущей системы на базе одной из микроконтроллерных платформ типа Arduino, Nucleo, Teensy, и др.
Что может быть проще? Давайте сделаем микроконтроллерную платформу для решения конкретной задачи – создание системы измерения давления и температуры, затрачивая меньше, возможно, средств, и используя все преимущества разработки программного обеспечения в среде Arduino Software (IDE).
Для этого, на аппаратном уровне, нам понадобятся компоненты:
- Arduino (Uno, …) – используем как программатор;
- микроконтроллер ATmega328P-PU – микроконтроллер будущей платформы;
- кварцевый резонатор на 16 МГц и пара керамических конденсаторов на 12-22 пФ каждый (по рекомендациям фирмы-изготовителя);
- тактовая кнопка на перезагрузку микроконтроллера и подтягивающий плюс питания к выводу RESET микроконтроллера резистор на 1 кОм;
- BMP180 — измерительный преобразователь температуры и давления с интерфейсом I2C;
- преобразователь интерфейсов TTL/USB;
- расходные материалы – провода, припой, монтажная плата, и др.
Принципиальная схема платформы, с учетом необходимых интерфейсов: стандартного последовательного интерфейса, I2C, и ничего более, представлена на рис. 1.
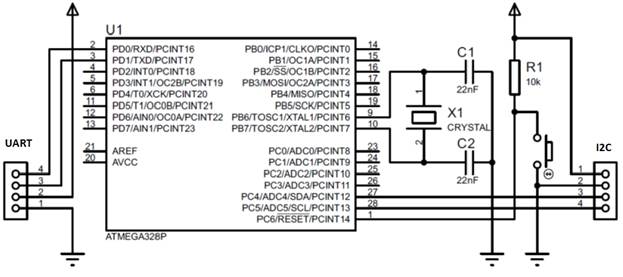
Рис. 1 — Принципиальная схема микроконтроллерной платформы для реализации системы измерения давления и температуры
Теперь рассмотрим этапы осуществления нашей задачи.
1. Прежде, нам нужен программатор. Подключаем Arduino (Uno, …) к компьютеру. В среде Arduno Software из меню по пути Файл->Примеры->11. ArdunoISP добираемся до программы программатора ArduinoISP, которую зашиваем в Arduino. Предварительно из меню Инструменты выбираем соответственно Плату, Процессор, Загрузчик, Порт.
После Загрузки программы ArduinoISP в плату, наша Arduino превращается в программатор и готова к использованию по назначению. Для этого в среде Arduno Software в меню Инструменты выбираем пункт Программатор: “Arduino as ISP”.
2. Подключаем по интерфейсу SPI ведомый микроконтроллер ATmega328P к ведущему программатору Arduino (Uno, …), рис. 2. Следует заметить, что предварительно биты регистра Low Fuse Byte микроконтроллера ATmega328P были установлены в незапрограммированное состояние.
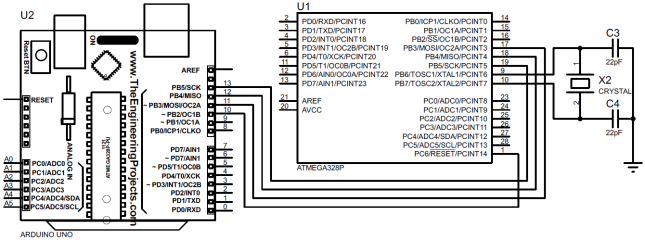
Рис. 2 – Схема подключения микроконтроллера к программатору
3. После успешной прошивки, микроконтроллер ATmega328P готов к установке на разработанную микроконтроллерную платформу (рис. 3), которую программируем также, как и полноценную Arduino (Uno, …). Программа опроса измерительного преобразователя давления и температуры представлена на листинге 1.

Рис. 3 Система измерения давления и температуры
Решение задач на плотность и молярный объём газов
Теоретический материал смотри на странице «Молярный объём газа«.
Основные формулы и понятния:
| Закон Авогадро При одинаковой температуре и давлении одинаковые объемы любых газов содержат одинаковое кол-во молекул Если V1=V2; T1=T2; P1=P2, то N1=N2 |
Из закона Авогадро, например, следует, что при одинаковых условиях в 1 литре водорода и в 1 литре кислорода содержится одинаковое кол-во молекул, хотя их размеры сильно разнятся.
Первое следствие из закона Авогадро:
| При одинаковых условиях 1 моль любого газа занимает один и тот же объём Если N1=N2; T1=T2; P1=P2, то V1=V2 |
Объём, который занимает 1 моль любого газа при нормальных условиях (н.у.), равен 22,4 литра и называется молярным объёмом газа (Vm).
Vm=V/ν (м3/моль)
Что называют нормальными условиями (н.у.):
- нормальная температура = 0°C или 273 К;
- нормальное давление = 1 атм или 760 мм рт.ст. или 101,3 кПа
Из первого следствия закона Авогадро вытекает, что, например, 1 моль водорода (2 г) и 1 моль кислорода (32 г) занимают один и тот же объем, равный 22,4 литра при н.у.
Зная Vm, можно найти объем любого кол-ва (ν) и любой массы (m) газа:
V=Vm·ν V=Vm·(m/M)
Типовая задача 1: Какой объём при н.у. занимает 10 моль газа?
V=Vm·ν=22,4·10=224 (л/моль)
Типовая задача 2: Какой объём при н.у. занимает 16 г кислорода?
V(O2)=Vm·(m/M) Mr(O2)=32; M(O2)=32 г/моль V(O2)=22,4·(16/32)=11,2 л
Второе следствие из закона Авогадро:
| Относительная плотность одного газа по другому газу равна отношению их молярных или относительных молекулярных масс DY(X) = M(X)/M(Y) = Mr(X)/MrY |
Зная пллотность газа (ρ=m/V) при н.у., можно вычислить молярную массу этого газа: M=22,4·ρ
Плотностью (D) одного газа по другому называют отношение массы определённого объёма первого газа к массе аналогичного объёма второго газа, взятого при одинаковых условиях.
Типовая задача 3: Определить относительную плотность углекислого газа по водороду и воздуху.
Dводород(CO2) = Mr(CO2)/Mr(H2) = 44/2 = 22 Dвоздух = 44/29 = 1,5
| Закон объёмных отношений при одинаковых условиях отношение объёмов газов (а также объёмы газообразных продуктов), которые вступают в реакцию, соотносятся, как небольшие целые числа, коэффициенты в уравнениях реакций показывают числа объёмов реагировавших и образовавшихся газов |
- один объём водорода и один объём хлора дают два объёма хлористого водорода: H2 Cl2=2HCl
- два объёма водорода и один объём кислорода дают два объёма водяного пара: 2H2 O2=2H2O
Задача 1. Сколько молей и молекул содержится в 44 г углекислого газа.
Решение:
M(CO2)=12 16·2=44 г/моль ν = m/M = 44/44 = 1 моль N(CO2) = ν·NA = 1·6,02·1023 = 6,02·1023
Задача 2. Вычислить массу одной молекулы озона и атома аргона.
Решение:
M(O3) = 16·3 = 48 г m(O3) = M(O3)/NA = 48/(6,02·1023) = 7,97·10-23г M(Ar) = 40 г m(Ar) = M(Ar)/NA = 40/(6,02·1023) = 6,65·10-23г
Задача 3. Какой объём при н.у. занимает 2 моля метана.
Решение:
ν = V/22,4 V(CH4) = ν·22,4 = 2·22,4 = 44,8 л
Задача 4. Определить плотность и относительную плотность оксида углерода (IV) по водороду, метану и воздуху.
Решение:
Mr(CO2)=12 16·2=44; M(CO2)=44 г/моль Mr(CH4)=12 1·4=16; M(CH4)=16 г/моль Mr(H2)=1·2=2; M(H2)=2 г/моль Mr(воздуха)=29; М(воздуха)=29 г/моль ρ=m/V ρ(CO2)=44/22,4=1,96 г/моль D(CH4)=M(CO2)/M(CH4)=44/16=2,75 D(H2)=M(CO2)/M(H2)=44/2=22 D(воздуха)=M(CO2)/M(воздуха)=44/24=1,52
Задача 5. Определить массу газовой смеси, в которую входят 2,8 кубометров метана и 1,12 кубометров оксида углерода.
Решение:
Mr(CO2)=12 16·2=44; M(CO2)=44 г/моль Mr(CH4)=12 1·4=16; M(CH4)=16 г/моль 22,4 кубометра CH4 = 16 кг 2,8 кубометра CH4 = x m(CH4)=x=2,8·16/22,4=2 кг 22,4 кубометра CO2 = 28 кг 1,12 кубометра CO2 = x m(CO2)=x=1,12·28/22,4=1,4 кг m(CH4) m(CO2)=2 1,4=3,4 кг
Задача 6. Определить объёмы кислорода и воздуха требуемые для сжигания 112 кубометров двухвалентного оксида углерода при содержании в нем негорючих примесей в объёмных долях 0,50.
Решение:
- определяем объём чистого CO в смеси:
V(CO)=112·0,5=66 кубометров
- определяем объём кислорода, необходимый для сжигания 66 кубов CO:
2CO O2=2CO2 2моль 1моль 66м3 X м3 V(CO)=2·22,4 = 44,8 м3 V(O2)=22,4 м3 66/44,8 = X/22,4 X = 66·22,4/44,8 = 33 м3 или 2V(CO)/V(O2) = V0(CO)/V0(O2) V - молярные объемы V0 - вычисляемые объемы V0(O2) = V(O2)·(V0(CO)/2V(CO))
Задача 7. Как изменится давление в сосуде, заполненном газами водорода и хлора после того, как они вступят в реакцию? Аналогично для водорода и кислорода?
Решение:
- H2 Cl2=2HCl — в результате взаимодействия 1 моля водорода и 1 моля хлора получается 2 моля хлороводорода: 1(моль) 1(моль)=2(моль), следовательно, давление не изменится, поскольку получившийся объм газовой смеси равен сумме объемов компонентов, вступивших в реакцию.
- 2H2 O2=2H2O — 2(моль) 1(моль)=2(моль) — давление в сосуде уменьшится в полтора раза, поскольку из 3 объёмов компонентов, вступивших в реакцию, получилось 2 объёма газовой смеси.
Задача 8. 12 литров газовой смеси из аммиака и четырехвалентного оксида углерода при н.у. имеют массу 18 г. Сколько в смеси каждого из газов?
Решение:
V(NH3)=x л V(CO2)=y л M(NH3)=14 1·3=17 г/моль M(CO2)=12 16·2=44 г/моль m(NH3)=x/(22,4·17) г m(CO2)=y/(22,4·44) г Система уравнений объем смеси: x y=12 масса смеси: x/(22,4·17) y/(22,4·44)=18 После решения получим: x=4,62 л y=7,38 л
Задача 9. Какое кол-во воды получится в результате реакции 2 г водорода и 24 г кислорода.
Решение:
2H2 O2=2H2O
Из уравнения реакции видно, что кол-ва реагирующих веществ не соответствуют отношению стехиометрических коэффициентов в уравнении. В таких случаях вычисления проводят по веществу, которого меньше, т.е., это вещество закончится первым в ходе реакции. Чтобы определить какой из компонентов находится в недостатке, надо обратить внимание на коэффициенте в уравнении реакции.
Количества исходных компонентов ν(H2)=4/2=2 (моль) ν(O2)=48/32=1,5 (моль)
Однако, торопиться не надо. В нашем случае для реакции с 1,5 моль кислорода необходимо 3 моль водорода (1,5·2), а у нас его только 2 моль, т.е., не хватает 1 моль водорода, чтобы прореагировали все полтора моля кислорода. Поэтому, расчёт кол-ва воды будем вести по водороду:
ν(H2O)=ν(H2)=2 моль m(H2O) = 2·18=36 г
Задача 10. При температуре 400 К и давлении 3 атмосферы газ занимает объём 1 литр. Какой объем будет занимать этот газ при н.у.?
Решение:
Из уравнения Клапейрона:
P·V/T = Pн·Vн/Tн Vн = (PVTн)/(PнT) Vн = (3·1·273)/(1·400) = 2,05 л
Таблица. относительные плотности газов по воздуху по возрастанию в т.ч. горючих и опасных плотности газов, химические формулы газов и молекулярные веса. — инженерный справочник / технический справочник дпва / таблицы для инженеров (ex dpva-info)
1)NTP — Нормальная температура и давление (Normal Temperature and Pressure) — 20oC (293.15 K, 68oF) при 1 атм ( 101.325 кН/м2, 101.325 кПа, 14.7 psia, 0 psig, 30 in Hg, 760 мм.рт.ст)
2)STP — Стандартная температура и давление (Standard Temperature and Pressure) — 0oC (273.15 K, 32oF) при 1 атм (101.325 кН/м2, 101.325 кПа, 14.7 psia, 0 psig, 30 in Hg, 760 torr=мм.рт.ст)
Уравнение клапейрона-менделеева. связь между числом молей газа, его температурой, объемом и давлением.
Теперь немного формул.
где P — давление газа (например, в атмосферах) V — объем газа (в литрах); T — температура газа (в кельвинах); R — газовая постоянная (0,0821 л·атм/моль·K). Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль
Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также
где n — число молей газа
И как нетрудно заметить, соотношение
есть величина постоянная для одного и того же количества моль газа.
И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.
Так, закон Бойля-Мариотта гласит (это два человека): Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.
Закон Гей-Люссака (а вот это один человек): Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры
Закон Шарля: Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры
Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.
Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Заключение
Газовые законы — серьезная тема школьного курса физики, которую более подробно разбирают на первом году обучения в вузах. Комбинированный закон газа прост на первый взгляд, но обилие параметров может запутать школьника, а выведение пропорций и вовсе способно превратить задачу в ад. Для упрощения расчетов используйте наш онлайн-калькулятор, не забывая переводить все заданные параметры в систему СИ.
Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:
Выводы
Разработана методика определения плотности газа по результатам измерения давления и температуры с применением датчиков Arduino и программных средств Python.