Основное уравнение молекулярно-кинетической теории газов. внутренняя энергия идеального газа
1. Основное уравнение молекулярно-кинетической теории идеальных газов
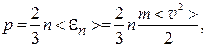
где n – концентрация молекул газа; <en> – средняя энергия поступательного движения одной молекулы; m – масса молекулы; <v2> – среднее значение квадрата скорости.
2. Средняя кинетическая энергия, приходящаяся на одну степень свободы
< e1 >= 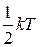 .
.
3. Средняя кинетическая энергия молекулы
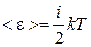 ,
,
где k = R/NА = 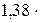 10-23 Дж/К – постоянная Больцмана; i – число степеней свободы молекулы.
10-23 Дж/К – постоянная Больцмана; i – число степеней свободы молекулы.
Для одноатомного газа i = 3; для двухатомного газа i = 5; для трёх и более атомных газов i = 6.
4. Внутренняя энергия произвольной массы идеального газа:
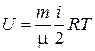 .
.
5. Зависимость давления газа от концентрации молекул и абсолютной температуры
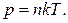
Примеры решения задач
Задача 1
Давление в сосуде с водородом равно 0,266 МПа. При этом средняя квадратичная скорость молекул равна 1400 м/с. Определить число молекул водорода в 1 см3.
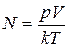 . (2)
. (2)
Неизвестную температуру Т определим, используя выражение для средней кинетической энергии поступательного движения молекулы
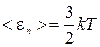 . (3)
. (3)
Приравняем 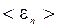 выражению для кинетической энергии молекулы
выражению для кинетической энергии молекулы
 , (4)
, (4)
где масса молекулы водорода 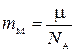 .
.
Из формулы (4) выразим Т:
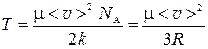 , (5)
, (5)
Подставив выражение (5) в формулу (2) и учитывая, что 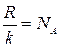 , получим:
, получим:
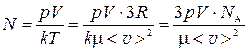 .
.
Проведем вычисления:
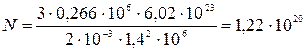 молекул.
молекул.
Задача 2
Кислород массой 1 кг находится при температуре 320 К. Определить 1) внутреннюю энергию газа; 2) среднюю кинетическую энергию вращательного движения молекул кислорода. Газ считать идеальным.
Кислород – двухатомный газ, для него полное число степеней свободы его молекул i = 5, из них 3 степени свободы приходятся на поступательное, а две – на вращательное движение
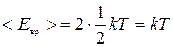 , (2)
, (2)
в данной массе газа содержится N молекул,
где
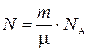 . (3)
. (3)
Средняя кинетическая энергия вращательного движения всех N молекул
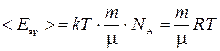 . (4)
. (4)
Проведем вычисления внутренней энергии по формуле (1), подставив в неё исходные данные:
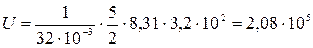 Дж = 208 кДж.
Дж = 208 кДж.
Проведем вычисление <Eвр> по формуле (4):
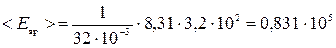 Дж = 83,1 кДж.
Дж = 83,1 кДж.
Элементы классической статистики
1. Скорости молекул:
— cредняя квадратичная
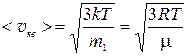 ,
,
— cредняя
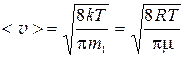 ,
,
— наиболее вероятная
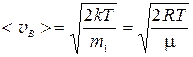 ,
,
где m1– масса молекулы, равная
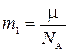 .
.
2. Средняя длина свободного пробега молекул газа
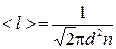 ,
,
где d – эффективный диаметр молекулы.
3. Среднее число соударений, испытываемых одной молекулой газа в единицу времени,
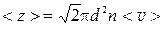 ,
,
где 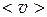 – средняя скорость молекул.
– средняя скорость молекул.
4. Барометрическая формула, выражающая зависимость давления идеального газа от высоты h над поверхностью Земли,
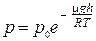
где p – давление газа на высоте h, p0– давление газа на высоте h = 0, Т – абсолютная температура воздуха на высоте h = 0.
Примеры решения задач
Задача 1
При температуре 300 К и некотором давлении средняя длина свободного пробега молекул кислорода равна 0,1 мкм. Чему равно среднее число столкновений, испытываемых молекулами в 1 с, если сосуд откачать до 0,1 первоначального давления? Температуру газа считать постоянной.
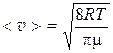 , (2)
, (2)
<l> – средняя длина свободного пробега.
Так как 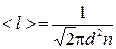 , а давление р = nkT, то длина свободного пробега молекул пропорциональна давлению.
, а давление р = nkT, то длина свободного пробега молекул пропорциональна давлению.
Тогда 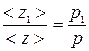 , т.е.
, т.е.
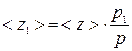 . (3)
. (3)
Подставив в формулу (3) выражение для <z>, получим:
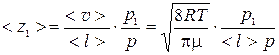 . (4)
. (4)
Проведем вычисления, подставив в формулу (4) числовые значения
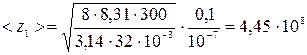 с-1.
с-1.
Задача 2
На сколько отличается атмосферное давление на вершине горы высотой 830 м от давления у подножия горы, если у подножия оно равно 100 кПа, а температура воздуха равна 290 К и не изменяется с высотой.
где р – атмосферное давление на вершине горы; р0 – давление у ее подножия; h – высота горы; Т – термодинамическая температура.
Находим искомое изменение давления
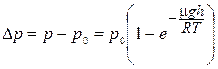 .
.
Воспользуемся разложением функции еxв ряд Тейлора и ограничимся первыми членами разложения, так как показатель экспоненты 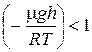 .
.
Получим:
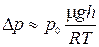 .
.
Произведем расчет, используя табличные данные:
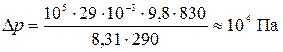 .
.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
1. Первое начало термодинамики
Q = DU A,
где Q – количество теплоты, сообщенное системе; DU – изменение внутренней энергии системы; A – работа.
2. Молярная теплоемкость газа при постоянном объёме
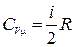 .
.
3. Молярная теплоёмкость газа при постоянном давлении
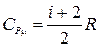 ,
,
где i – число степеней свободы молекулы газа.
4. Связь между удельной (c) и молярной Cm теплоемкостями
Cm= cm.
5. Внутренняя энергия идеального газа
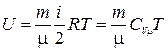 .
.
6. Работа расширения газа в изотермическом процессе
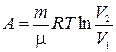 ,
,
7. Работа расширения газа в изобарном процессе
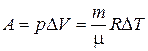 .
.
8. Работа расширения в адиабатном процессе
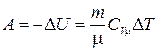 или
или 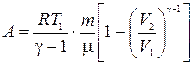 ,
,
где  – показатель адиабаты.
– показатель адиабаты.
9. Уравнение состояния адиабатного процесса (уравнение Пуассона).
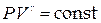 .
.
Примеры решения задач
Задача 1
Кислород массой 2 кг занимает объем 1 м3 и находится под давлением 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема 3 м3, а затем при постоянном объеме до давления 0,5 МПа. Найти изменение внутренней энергии газа, совершенную им работу и теплоту, переданную газу. Построить график процесса.
Начальную и конечную температуру газа найдем из уравнения Менделеева-Клапейрона
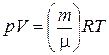 ,
,
откуда
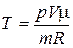 .
.
Работа расширения газа при постоянном давлении выражается формулой
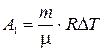 .
.
Работа газа, нагреваемого при постоянном объеме, равна нулю
A2 = 0.
Следовательно, полная работа, совершаемая газом,
A = A1 A2= A1.
Согласно первому началу термодинамики, теплота Q1, переданная газу, равна сумме изменения внутренней энергии DU и работы A
Q = DU A.
Произведем вычисления, учитывая, что для кислорода m = 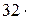 10-3 кг/моль
10-3 кг/моль
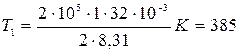 K;
K;
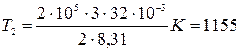 K;
K;
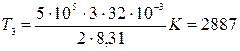 K;
K;
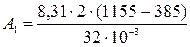 Дж = 0,4 . 106 Дж = 0,4 МДж;
Дж = 0,4 . 106 Дж = 0,4 МДж;
A = A1= 0,4 МДж;
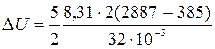 Дж = 3,24 . 106 Дж = 3,24 МДж;
Дж = 3,24 . 106 Дж = 3,24 МДж;
Q = (3,24 0,4) МДж = 3,64 МДж.
График процесса приведен на рис 1.
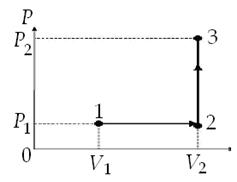
Рис.1
Задача 2
Чему равны удельные теплоемкости cV и сp некоторого двухатомного газа, если плотность этого газа при нормальных условиях равна 1,43 кг/м3?
так как плотность газа r = m / V.
Подставляя молярную массу в формулы для теплоемкости, имеем
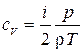 и
и 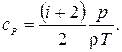
Произведем вычисления, учитывая, что для двухатомного газа число степеней свободы i = 5. Так как при нормальных условиях давление p = 1,01 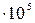 Па и T = 273 K, находим
Па и T = 273 K, находим
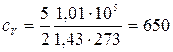 Дж/(кг
Дж/(кг 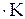 ),
), 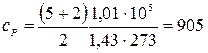 Дж/(кг
Дж/(кг 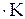 ).
).
Круговые процессы. КПД цикла. Цикл Карно
1. Коэффициент полезного действия тепловой машины
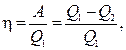
где А – работа, совершенная в цикле, А = Q1 – Q2; Q1 – количество теплоты, полученное рабочим телом от теплоотдатчика; Q2 – количество теплоты, отданное рабочим телом теплоприемнику.
2. КПД цикла Карно
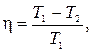
где T1– температура теплоотдачика; T2 – температура теплоприемника.
3. Так как 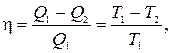 то
то 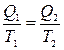 , то есть приведенная теплота
, то есть приведенная теплота 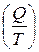 для любых изотермических переходов между двумя адиабатами есть величина постоянная.
для любых изотермических переходов между двумя адиабатами есть величина постоянная.
Примеры решения задач
Задача 1
Идеальный газ совершает цикл Карно. Газ получил от теплоотдатчика количество теплоты 5,5 кДж и совершил за цикл работу 1,1 кДж. Определить: 1) термический КПД цикла; 2) отношение температур теплоотдатчика и теплоприёмника.
КПД цикла Карно
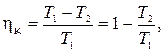
так как газ совершает цикл Карно, то
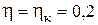 ;
; 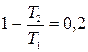 , тогда
, тогда 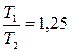 ,
,
то есть температура теплоотдатчика в 1,25 раз выше температуры теплоприёмника.
Энтропия
1. Изменение энтропии системы при переходе из состояния 1 в состоя- ние 2
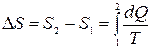 ,
, 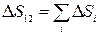 ,
,
где 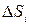 – изменение энтропии в промежуточных процессах.
– изменение энтропии в промежуточных процессах.
Примеры решения задач
Задача 1
Найти изменение энтропии при превращении 10 г льда при –20 оС в пар при 100 оС.
В данном случае общее изменение энтропии DS складывается из изменений ее в отдельных процессах:
а) Нагревание массы m льда от температуры T1 до температуры T2, при этом
dQ = mc1dT,
где c1 – удельная теплоемкость льда.
Тогда изменение энтропии в этом процессе
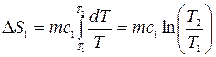 ,
,
здесь Т2 = 273 К – температура таяния льда.
в) Плавление массы m льда при температуре T2
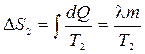 ,
,
где l – удельная теплота плавления.
с) Нагревание массы m воды от T2 до T3. Аналогично пункту а) получаем
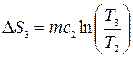 ,
,
где с2 – удельная теплоемкость воды.
d) Испарение массы m воды при температуре T3

где r – удельная теплота парообразования.
Общее изменение энтропии
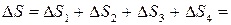
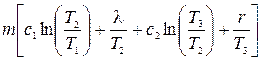 .
.
Произведем вычисления, используя табличные данные
c1 = 2,1 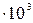 Дж/кг
Дж/кг 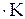 , T1 = 253 K, T2= 273 K, T3 = 373 K, l = 3,35
, T1 = 253 K, T2= 273 K, T3 = 373 K, l = 3,35 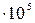 Дж / кг, с2 = 4,19
Дж / кг, с2 = 4,19 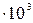 Дж/(кг.К), r = 2,26
Дж/(кг.К), r = 2,26 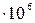 Дж /кг и получим DS = 88 Дж /К.
Дж /кг и получим DS = 88 Дж /К.
Задание на контрольную работу №2
201. Какова плотность воздуха в цилиндре дизельного двигателя в конце такта сжатия, если температура 677 оС, а давление 5,05 МПа? Молярную массу воздуха считать равной 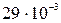 кг/моль.
кг/моль.
202. Определить концентрацию молекул кислорода, находящегося в сосуде объемом 2 л. Количество вещества равно 0,2 моль.
203. На сколько изменится давление воздуха в шине автомобиля при повышении температуры до 30 оС, если при температуре 10 оС давление равно допустимому значению 238 кПа?
204. Сосуд объемом 10 л содержит гелий под давлением 1 МПа и при температуре 300 К.После того, как из баллона выпущено 10 г гелия, температура в баллоне понизилась до 290 К.Определить давление гелия, оставшегося в баллоне.
205. В сосуде ёмкостью 5 л при нормальных условиях находится азот. Определить: 1) количество вещества; 2) массу азота; 3) концентрацию его молекул в сосуде.
206. В дизеле в начале такта сжатия температура воздуха 40 оС, а давление 78,4 кПа. Во время сжатия объем уменьшается в 15 раз, а давление возрастает до 3,5 Мпа. Определить температуру воздуха в конце такта сжатия.
207. Автомобильная шина накачана воздухом до давления 0,3 МПа при температуре 7 оС. Какое количество воздуха необходимо выпустить из камеры, чтобы давление не изменилось при повышении температуры до 37 оС? Объем камеры 50 л.
208. Альпинист при каждом вдохе поглощает 5 г воздуха, находящегося при нормальных условиях. Найти объем воздуха, который должен вдыхать за то же время альпинист в горах, где давление равно 79,8 кПа, а температура – 13 оС.
209. Какое число баллонов водорода емкостью 50 л при температуре 27 оС и давлении 4 МПа потребуется для заполнения аэростата объемом 103 м3, если при температуре 7 оС давление в нём должно быть 100 кПа?
210. Кислород массой 10 г находится под давлением 0,3 МПа при температуре 10 оС. После расширения вследствие нагревания при постоянном давлении кислород занял объем 10 л. Определить: 1) объём газа до расширения; 2) температуру газа после расширения; 3) плотность газа до расширения; 4) плотность газа после расширения.
211. Баллон, содержащий 1 кг азота, при испытании взорвался при температуре 350 оС. Какое количество водорода можно хранить в этом баллоне при 20 оС, имея пятикратный запас прочности?
212. Два сосуда, содержащие одинаковые массы одного газа, соединены трубкой с краном. В первом сосуде давление 5 кПа, во втором 8 кПа. Какое давление установится после открытия крана, если температура останется неизменной?
213. Баллон ёмкостью 0,3 л содержит смесь водорода и гелия при температуре 300 К и давлении 0,82 МПа. Масса смеси 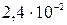 кг. Определить массы водорода и гелия.
кг. Определить массы водорода и гелия.
214. Определить плотность смеси, состоящей из 4 г гелия и 28 г азота при температуре 27 оС и давлении 1 МПа.
215. До какого давления накачан футбольный мяч ёмкостью 3 л, если при этом сделано 40 качаний поршневого насоса. За каждое качание насос захватывает из атмосферы 150 см3 воздуха. Мяч вначале был пустой. Атмосферное давление 0,1 МПа.
216. Определить молярную массу газа, свойства которого соответствуют свойствам смеси 160 г кислорода и 120 г азота.
217. В сосуде объемом 20 л при температуре 27 оС находится смесь кислорода массой 6 г и углекислого газа массой 66 г. Определить давление смеси.
218. Определить плотность смеси 4 г водорода и 32 г кислорода при температуре 7 оС и давлении 100 кПа.
219. Какой объем занимает смесь азота массой 1 кг и гелия массой 1 кг при нормальных условиях?
220. Газовая смесь, состоящая из кислорода и азота, находится в баллоне под давлением 1 МПа. Считая, что масса кислорода составляет 20 % от массы смеси, определить парциальные давления отдельных газов.
221. Определить среднюю кинетическую энергию поступательного движения молекул газа, находящегося под давлением 0,2 Па. Концентрация молекул газа равна 1013 см-3.
222. Сколько молекул кислорода содержится в сосуде объемом 10 см3, если при тепловом хаотическом движении со средней квадратичной скоростью 400 м/с они производят на стенке сосуда давление 1 кПа?
223. Газ занимает объем 1 л под давлением 2 кПа. Определить кинетическую энергию поступательного движения всех молекул, находящихся в данном объеме.
224. 1 кг двухатомного газа находится под давлением 80 кПа и имеет плотность 4 кг/м3. Найти энергию теплового движения молекул газа в этих условиях.
225. Определить энергию теплового движения молекул аммиака NH3, находящихся в баллоне объёмом 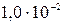 м3 при давлении 2,57 кПа. Какую часть от этой энергии составляет средняя энергия вращательного движения молекул? Молекулы считать жесткими.
м3 при давлении 2,57 кПа. Какую часть от этой энергии составляет средняя энергия вращательного движения молекул? Молекулы считать жесткими.
226. Определить среднюю энергию вращательного движения одной молекулы двухатомного газа, если суммарная кинетическая энергия молекул одного киломоля этого газа равна 3,01 МДж.
227. Баллон с водородом двигался со скоростью 50 м/с и внезапно остановился. На сколько градусов нагреется при этом газ?
228. Определить внутреннюю энергию 1 кг воздуха в шине автомобиля при допустимом давлении 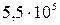 Па и плотности воздуха в шине 4 кг/м3. Воздух считать двухатомным газом.
Па и плотности воздуха в шине 4 кг/м3. Воздух считать двухатомным газом.
229. Средняя энергия поступательного движения молекул азота, находящегося в баллоне объёмом 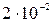 м3 равна
м3 равна 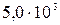 Дж, а средняя квадратичная скорость его молекул
Дж, а средняя квадратичная скорость его молекул 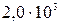 м/с. Определить: 1) количество молекул в баллоне; 2) давление, под которым находится азот.
м/с. Определить: 1) количество молекул в баллоне; 2) давление, под которым находится азот.
230. Какое число молекул двухатомного газа занимает объем 10 см3 при давлении 5,32 кПа и температуре 27 оС? Какой энергией теплового движения обладают эти молекулы?
231. Определить давление в камере сгорания дизельного двигателя объёмом 0,08 л в конце сжатия, если средняя квадратичная скорость молекул воздуха в это время 1 км/с, а масса воздуха в камере сгорания 1,2 г.
232. Определить среднюю скорость молекул газа, если известно, что их средняя квадратичная скорость равна 1 км/с.
233. Определить наиболее вероятную скорость молекул газа, плотность которого при давлении 40 кПа составляет 0,35 кг/м3.
234. Средняя квадратичная скорость некоторого газа при нормальных условиях равна 500 м/с. Сколько молекул содержит 1 г этого газа?
235. Определить среднюю длину свободного пробега молекул водорода при температуре 27 оС и давлении 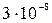 Па (эффективный диаметр молекулы водорода принять равным
Па (эффективный диаметр молекулы водорода принять равным 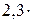 10-10 м).
10-10 м).
236. Баллон емкостью 10 л содержит азот массой 1 г. Определить среднюю длину свободного пробега молекул (эффективный диаметр молекулы азота принять равным 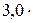 10-10 м).
10-10 м).
237. Определить среднюю длину свободного пробега молекул кислорода, находящегося при температуре 0 оС, если среднее число столкновений, испытываемых молекулой в 1 с, равно 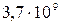 .
.
238. На сколько изменится атмосферное давление при подъеме на высоту 100 м над уровнем моря, если давление на уровне моря равно 100 кПа. Считать, что температура равна 290 К и не изменяется с высотой.
239. Найти время свободного пробега молекул водорода при давлении 0,1 Па и температуре 100 К (эффективный диаметр молекулы водорода принять равным 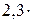 10-10 м).
10-10 м).
240. На какой высоте давление воздуха составляет 60 % от давления на уровне моря? Считать, что температура воздуха не изменяется с высотой и равна 10 оС.
241. При адиабатическом расширении азот массой 10 г совершает работу, равную 321 Дж. На сколько уменьшилась внутренняя энергия и понизилась температура азота, если его удельная теплоемкость при постоянном объеме 742 Дж/( 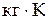 ).
).
242. В закрытом сосуде объемом 2 л находится азот, плотность которого 1,4 кг/м3. Какое количество теплоты надо сообщить азоту, чтобы нагреть его на 100 К? На сколько увеличится внутренняя энергия азота?
243. Азот массой 1 кг занимает при температуре 300 К объем 0,5 м3. В результате адиабатического сжатия давление газа увеличилось в 3 раза. Определить: 1) конечный объем газа; 2) его конечную температуру; 3) изменение внутренней энергии газа.
244. Во сколько раз увеличится объем 0,4 моля водорода при изотермическом расширении, если при этом газ получил количество теплоты 800 Дж? Температура водорода 27 оС. Чему равна работа расширения?
245. Водород массой 6,5 г, находящийся при температуре 27 оС, расширяется вдвое при постоянном давлении за счет притока извне тепла. Найти работу расширения газа, изменение внутренней энергии газа и количество теплоты, сообщенное газу.
246. Определить количество тепла, выделяющегося при изотермическом сжатии 7 г азота от нормального давления 0,1 МПа до 0,5 МПа. Температура азота 25 оС.
247. Определить работу изотермического расширения при сгорании одного моля смеси в цилиндре двигателя автомашины. Степень сжатия 6,5; температура сгорания смеси 2000 К. Смесь считать идеальным газом.
248. Кислород массой 10 г находится под давлением 0,3 МПа при температуре 10 оС. После нагревания при постоянном давлении объем газа равен 10 л. Найти количество теплоты, полученное газом, изменение его внутренней энергии и работу, совершенную газом.
249. Закрытый баллон емкостью 10 л, содержащий кислород при давлении 2 МПа и температуре 7 оС, нагревается до температуры 27 оС. Какое количество теплоты передано газу? На сколько увеличилась внутренняя энергия газа?
250. Воздух адиабатно сжимается от давления 0,1 МПа до 3,5 МПа. Начальная температура воздуха 40 оС. Найти температуру в конце такта сжатия.
251. Вычислить удельные теплоемкости при постоянном давлении и постоянном объеме неона и водорода, принимая эти газы за идеальные. Молярная масса неона  кг/моль, водорода
кг/моль, водорода 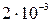 кг/моль.
кг/моль.
252. Определить удельную теплоёмкость некоторого одноатомного газа при постоянном объёме, если плотность этого газа при нормальных условиях 0,795 кг/м3.
253. Трехатомный газ под давлением 240 кПа и при температуре 20 оС занимает объем 10 л. Определить теплоемкость этого газа при постоянном давлении.
254. При температуре 207 оС масса 2,5 кг некоторого газа занимает объем 0,3 м3. Определить давление газа, если удельная теплоемкость при постоянном давлении равна 519 Дж/( 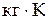 ) и g = Ср/CV= 1,67.
) и g = Ср/CV= 1,67.
255. Вычислить удельные теплоемкости газа, зная, что его молярная масса 44.10-3 кг/моль и отношение теплоемкостей g = Ср/CV= 1,33.
256. Известны удельные теплоемкости газа: сV= 649 Дж/( 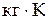 ) и сp = 912 Дж/(
) и сp = 912 Дж/( 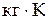 ). Найти молярную массу газа и число степеней свободы его молекул.
). Найти молярную массу газа и число степеней свободы его молекул.
257. Молярная масса газа равна 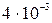 кг/моль. Отношение теплоемкостей Ср/CV= 1,67. Вычислить удельные теплоемкости газа.
кг/моль. Отношение теплоемкостей Ср/CV= 1,67. Вычислить удельные теплоемкости газа.
258. Определить удельные теплоёмкости для смеси газов, содержащих гелий массой 1 г и водород массой 4 г.
259. Некоторый газ находится при температуре 350 оК в баллоне емкостью 100 л под давлением 200 кПа. Теплоемкость этого газа при постоянном объеме 140 Дж/К. Определить отношение теплоемкостей Ср/CV.
260. Вычислить теплоемкость (при постоянном объеме) газа, заключенного в сосуд емкостью 20 л при нормальных условиях. Газ одноатомный.
261. В топке паровой турбины расходуется 0,35 кг дизельного топлива на 1 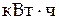 энергии. Температура поступающего в турбину пара 250 оС, температура теплоприемника 30 оС. Вычислить КПД турбины. Найти КПД идеальной тепловой машины, работающей при тех же температурных условиях. Удельная теплота сгорания топлива 42 Мдж/кг.
энергии. Температура поступающего в турбину пара 250 оС, температура теплоприемника 30 оС. Вычислить КПД турбины. Найти КПД идеальной тепловой машины, работающей при тех же температурных условиях. Удельная теплота сгорания топлива 42 Мдж/кг.
262. В ходе цикла Карно рабочее вещество получает от теплоотдатчика количество теплоты 300 кДж. Температуры теплоотдатчика и теплоприемника равны соответственно 480 К и 280 К. Определить термический КПД цикла и работу, совершаемую рабочим веществом за цикл.
263. Идеальная тепловая машина работает по циклу Карно, термический КПД которого 40 %. Температура теплоприемника 0 оС. Найти температуру теплоотдатчика и работу изотермического сжатия, если работа изотермического расширения 8 Дж.
264. Идеальной тепловой машиной за счет каждого килоджоуля теплоты, полученной от теплоотдатчика, за цикл совершается работа 300 Дж. Определить термический КПД машины и температуру теплоотдатчика, если температура теплоприемника 280 К.
265. У тепловой машины, работающей по циклу Карно, температура теплоотдатчика в 1,6 раза больше температуры теплоприемника. За цикл машина совершает работу 12 кДж. Найти термический КПД цикла и работу изотермического сжатия рабочего вещества за цикл.
266. Идеальный газ, совершающий цикл Карно, 70 % количества теплоты, полученного от теплоотдатчика, отдаёт теплоприёмнику. Количество теплоты, полученное от теплоотдатчика, равно 5 кДж. Определить: 1) термический КПД цикла; 2) работу цикла.
267. Идеальный газ совершает цикл Карно, термический КПД которого равен 0,4. Определить работу изотермического сжатия, если работа изотермического расширения составляет 400 Дж.
268. Температура теплоотдатчика идеальной тепловой машины 480 К, а ее КПД составляет 40 %. Чему равна температура теплоприемника? Какую долю количества теплоты, полученного от теплоотдатчика, газ отдает теплоприемнику?
269. Идеальная тепловая машина за цикл совершает работу 4 кДж, отдавая при этом теплоприёмнику 6,4 кДж теплоты. Определить КПД цикла, а также температуру теплоотдатчика, если температура теплоприемника 280 К.
270. Идеальный газ совершает цикл Карно. Газ получил от теплоотдатчика количество теплоты 5,5 кДж и совершил работу 1,1 кДж. Определить: 1) термический КПД цикла; 2) отношение температур теплоотдатчика и теплоприёмника.
271. Воду массой 1 г нагрели от температуры 10 оС до температуры 100 оС, при которой она вся превратилась в пар. Найти приращение энтропии системы.
272. Кусок льда массой 200 г, взятый при температуре -10 оС, был нагрет до 0 оС и расплавлен, после чего образовавшаяся вода была нагрета до температуры 10 оС. Определить изменение энтропии в ходе указанных процессов.
273. Кислород массой 10 г нагревается от температуры 50 оС до температуры 150 оС. Найти приращение энтропии, если нагревание происходит: а) изохорически; б) изобарически.
274. Во сколько раз при изотермическом процессе надо увеличить объем газа, чтобы его энтропия увеличилась на 23 Дж/К? Количество газа равно 4 моль.
275. В результате изохорического нагревания воздуха массой 1 г давление газа увеличилось в 2 раза. Определить изменение энтропии газа.
276. Смешано 5 кг воды при температуре 280 К и 8 кг воды при температуре 350 К. Найти: 1) температуру смеси; 2) изменение энтропии, происходящее при смешивании.
277. Объем кислорода массой 2 кг увеличился в 5 раз один раз в изотермическом процессе, другой раз – в адиабатическом процессе. Найти изменение энтропии в каждом из указанных процессов.
278. Идеальный газ количеством 1 моль сначала изобарно нагрели так, что его объем увеличился в 2 раза, а затем изохорно охладили так, что его давление уменьшилось в 2 раза. Определить приращение энтропии в ходе данных процессов.
279. Какова ёмкость системы охлаждения двигателя автомобиля, если при повышении температуры воды от 27 оС до 97 оС её энтропия увеличивается на 8,3 кДж/К.
280. При изотермическом процессе объем некоторого идеального газа увеличился в 2 раза, а энтропия возросла на 4,6 Дж/К. Какое количество газа участвовало в указанном процессе?
4. КОНТРОЛЬНАЯ РАБОТА № 3 “ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ”
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
В контрольную работу № 3 включены задачи по темам: электростатика, постоянный электрический ток, магнитостатика, электромагнитная индукция.
Перед выполнением контрольной работы необходимо проработать материал соответствующих разделов рекомендованной литературы, внимательно ознакомиться с основными законами и формулами, а также справочными материалами, приведенными в приложениях данной учебно-методической разработки. После этого надо разобрать примеры решения типовых задач из данной учебно-методической разработки и решить ряд задач из задачников по физике [4].
Задачи 301 … 330 относятся к теме “Электростатика”. Для решения этих задач необходимо изучить тему “Электростатика” по учебному пособию [1], с. 148…180.
Тема “Электростатика” представлена задачами по расчету простейших электрических полей с помощью принципа суперпозиции, на определение напряженности и разности потенциалов, электроемкости и энергии поля конденсаторов и задачами, в которых рассматривается движение заряженных частиц в электрическом поле.
Если электростатическое поле создано несколькими зарядами, то для нахождения напряженности 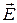 и потенциала
и потенциала 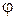 результирующего поля используют принцип суперпозиции. Напряженность поля системы зарядов равна векторной сумме напряженностей полей
результирующего поля используют принцип суперпозиции. Напряженность поля системы зарядов равна векторной сумме напряженностей полей 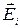 , созданным каждым зарядом в отдельности. При решении задачи делают чертёж и для данной точки поля указывают направление векторов
, созданным каждым зарядом в отдельности. При решении задачи делают чертёж и для данной точки поля указывают направление векторов 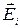 , векторы складывают по правилу сложения векторов. При расчёте напряженности знак заряда не учитывают.
, векторы складывают по правилу сложения векторов. При расчёте напряженности знак заряда не учитывают.
Потенциал результирующего поля системы зарядов равен алгебраической сумме потенциалов полей 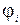 , созданных отдельными зарядами. Потенциал – скалярная величина, поэтому при расчёте потенциала знак заряда учитывается.
, созданных отдельными зарядами. Потенциал – скалярная величина, поэтому при расчёте потенциала знак заряда учитывается.
Если заряженное тело не является точечным зарядом, сферой, бесконечно длинным цилиндром, бесконечной плоскостью, то тело разбивается на бесконечно малые элементы (в случае нити или стержня элемент dr), которые можно считать точечными зарядами и по формуле для точечного заряда найти 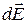 и
и 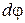 . Напряженность и потенциал находят интегрированием (интегрирование проводится по всей длине нити)
. Напряженность и потенциал находят интегрированием (интегрирование проводится по всей длине нити)
 и
и 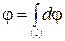 .
.
Силы взаимодействия точечных зарядов можно найти либо по закону Кулона и затем сложить силы по правилу сложения векторов, либо, используя соотношение 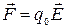 . Один из зарядов
. Один из зарядов  можно рассматривать как заряд, находящийся в электрическом поле, созданном другими зарядами.
можно рассматривать как заряд, находящийся в электрическом поле, созданном другими зарядами.
Если в условии задачи не указывается среда, в которой находятся заряды, то подразумевается вакуум 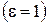 или воздух, диэлектрическая проницаемость которого близка к единице.
или воздух, диэлектрическая проницаемость которого близка к единице.
Для расчётов электрических полей при наличии диэлектрика вводят вспомогательный вектор – вектор электрической индукции (электрического смещения), который определяется по формуле 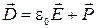 , где
, где 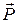 – поляризованность (вектор поляризации). Для однородных изотропных диэлектриков
– поляризованность (вектор поляризации). Для однородных изотропных диэлектриков 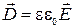 . В этом случае, если диэлектрики заполняют всё пространство или объем, ограниченный эквипотенциальными поверхностями (сюда относятся диэлектрики в плоских, цилиндрических и сферических конденсаторах), вектор
. В этом случае, если диэлектрики заполняют всё пространство или объем, ограниченный эквипотенциальными поверхностями (сюда относятся диэлектрики в плоских, цилиндрических и сферических конденсаторах), вектор 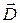 во всех точках поля как внутри, так и вне диэлектрика останется без изменения. Вектор напряженности
во всех точках поля как внутри, так и вне диэлектрика останется без изменения. Вектор напряженности 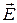 электрического поля внутри диэлектрика уменьшится в
электрического поля внутри диэлектрика уменьшится в 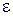 раз.
раз.
Задачи 331 … 340 относятся к теме “Постоянный электрический ток”. Приступая к решению этих задач, необходимо ознакомиться с данной темой по учебникам [1], с. 180…194. Следует учитывать, что на участке цепи, не содержащей ЭДС, напряжение U и разность потенциалов 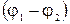 совпадают. Если в цепи имеется батарея из n одинаковых источников тока, то в законе Ома для замкнутой цепи надо использовать ЭДС батареи и внутреннее сопротивление батареи.
совпадают. Если в цепи имеется батарея из n одинаковых источников тока, то в законе Ома для замкнутой цепи надо использовать ЭДС батареи и внутреннее сопротивление батареи.
В задачах на определение работы и мощности тока следует иметь в виду, что полезная мощность выделяется во внешней цепи (на сопротивлении нагрузки), а полная мощность во всей цепи (на сопротивлении нагрузки и внутреннем сопротивлении источника); закон Джоуля-Ленца в форме 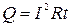 справедлив только для постоянного тока
справедлив только для постоянного тока
Задачи 341 … 370 относятся к теме “Магнитостатика”. Для решения этих задач необходимо ознакомиться с конкретными физическими понятиями, законами и формулами данной темы по учебному пособию [1], с. 204…212, 217…223, 212…216.
По теме “Магнитостатика” в контрольную работу включены задачи по расчету магнитной индукции и напряженности простейших магнитных полей с помощью принципа суперпозиции, задачи по расчету индукции магнитного поля с применением закона Био-Савара-Лапласа, задачи, в которых рассматривается действие магнитного поля на движущиеся заряды и токи (определение силы Ампера, силы Лоренца, вращающего момента, вычисление работы сил поля при перемещении проводника и контура с током).
Магнитное поле, созданное несколькими проводниками с током, рассчитывается с помощью принципа суперпозиции полей. Для решения задачи необходимо сделать чертёж, изобразить силовые линии магнитного поля для каждого проводника так, чтобы они проходили через точку, в которой надо определить индукцию. Векторы 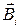 направлены по касательным к силовым линиям. Затем необходимо сложить векторы
направлены по касательным к силовым линиям. Затем необходимо сложить векторы 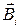 по правилу сложения векторов.
по правилу сложения векторов.
Задачи 371 … 380 относятся к теме “Электромагнитная индукция”. Приступая к решению этих задач, необходимо ознакомиться с данной темой по учебному пособию [1], с. 223…235.
В явлении электромагнитной индукции магнитный поток и потокосцепление через контур могут изменяться при движении контура в неоднородном магнитном поле, при вращении контура, при изменении площади контура, а также при изменении во времени магнитного поля.
Если в задаче требуется найти разность потенциалов на концах проводника, движущегося в магнитном поле, то надо иметь в виду, что искомая разность потенциалов численно равна ЭДС, индуцируемой в проводнике.
Табл. 3
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
4.2.1.Электростатика
1. Закон Кулона
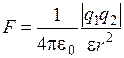 ,
,
где F – модуль силы взаимодействия точечных зарядов q1 и q2; r – расстояние между зарядами; e – относительная диэлектрическая проницаемость среды; e0 – электрическая постоянная (e0 = 8,85 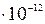 Ф/м).
Ф/м).
2. Напряженность и потенциал электростатического поля
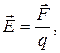
 ,
,
где 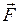 – сила, действующая на точечный положительный (пробный) заряд q, помещенный в данную точку поля; W – потенциальная энергия этого заряда.
– сила, действующая на точечный положительный (пробный) заряд q, помещенный в данную точку поля; W – потенциальная энергия этого заряда.
3. Напряженность и потенциал поля, создаваемого системой зарядов (принцип суперпозиции электрических полей),
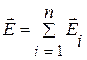 ;
;  ,
,
где 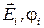 – напряженность и потенциал в данной точке поля, создаваемого i-м зарядом.
– напряженность и потенциал в данной точке поля, создаваемого i-м зарядом.
4. Напряженность и потенциал поля, создаваемого точечным зарядом,
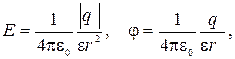
где r – расстояние от заряда q до точки, в которой определяются напряженность и потенциал.
5. Напряженность поля, создаваемого бесконечной равномерно заряжен-ной плоскостью
Е = 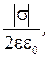
где s – поверхностная плотность заряда (заряд единицы площади).
6. Напряженность поля, создаваемого бесконечной равномерно заряжен-ной нитью или бесконечно длинным цилиндром (вне цилиндра),
Е = 
где t – линейная плотность заряда, r – расстояние от нити или от оси цилиндра до точки, в которой вычисляется напряженность. Внутри цилиндра Е = 0.
7. Напряженность и потенциал поля, создаваемого металлической заряженной сферой радиусом R на расстоянии r от центра сферы:
а) внутри сферы (r<R)
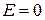 ;
; 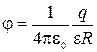 ;
;
б) вне сферы (r 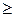 R)
R)
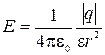 ;
; 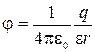 ,
,
где q – заряд сферы.
8. Связь потенциала с напряженностью в случае однородного поля
E = (j1 – j2)/d,
где d – расстояние между точками с потенциалами j1 и j2.
9. Работа сил поля по перемещению точечного заряда q из точки поля с потенциалом j1 в точку поля с потенциалом j2
A= q (j1 – j2).
10. Поток напряженности 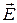 и электрического смещения (индукции)
и электрического смещения (индукции) 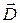 :
:
а) через произвольную поверхность S, помещенную в неоднородное поле,
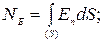
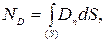
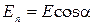 и
и 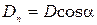 – проекции векторов
– проекции векторов 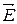 и
и 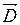 на направление нормали
на направление нормали  ;
; 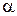 – угол между векторами
– угол между векторами 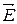 или
или 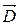 и нормалью
и нормалью  .
.
б) через плоскую поверхность, помещенную в однородное поле,
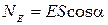 ,
, 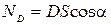 .
.
Поток векторов 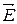 и
и 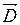 через любую замкнутую поверхность (теорема Гаусса):
через любую замкнутую поверхность (теорема Гаусса):
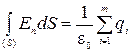 ;
; 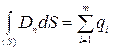 ,
,
где 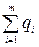 – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности S; m – число зарядов.
– алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности S; m – число зарядов.
Электрическое поле рассматривается в вакууме.
11. Связь электрического смещения (индукции) 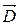 с напряженностью
с напряженностью 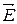 в случае изотропных диэлектриков
в случае изотропных диэлектриков
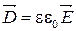 .
.
12. Электроемкость
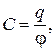
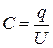 ,
,
где j – потенциал уединённого проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю); U = (j1 – j2) – разность потенциалов между обкладками конденсатора.
13. Электроемкость плоского конденсатора
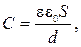
где S – площадь одной пластины конденсатора; d – расстояние между пластинами; e – диэлектрическая проницаемость среды, заполняющей пространство между пластинами.
15. Электроемкость сферического конденсатора
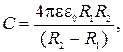
где  и
и 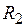 – радиусы двух концентрических сфер;
– радиусы двух концентрических сфер; 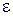 – диэлектрическая проницаемость среды, заполняющей пространство между сферами.
– диэлектрическая проницаемость среды, заполняющей пространство между сферами.
16. Электроемкость цилиндрического конденсатора
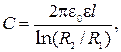
где  и
и 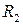 – радиусы двух коаксиальных цилиндров; l — высота цилиндров;
– радиусы двух коаксиальных цилиндров; l — высота цилиндров; 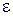 – диэлектрическая проницаемость среды, заполняющей пространство между цилиндрами.
– диэлектрическая проницаемость среды, заполняющей пространство между цилиндрами.
17. Электроемкость параллельно и последовательно соединенных конденсаторов
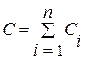 ;
; 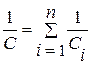 ,
,
где n – число конденсаторов в батарее.
18. Энергия заряженного конденсатора
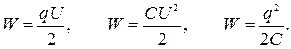
19. Объемная плотность энергии электрического поля
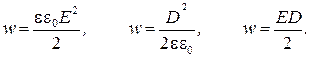
Для однородного электрического поля w = W/V, где V – объем.
Примеры решения задач
Задача 1
Два точечных заряда 2 нКл и –1 нКл находятся в воздухе на расстоянии 5 см друг от друга. Определить напряженность и потенциал электростатического поля в точке, удаленной от первого заряда на расстояние 6 см и от второго заряда на 4 см.
Согласно принципу суперпозиции электрических полей, каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Напряженность результирующего поля 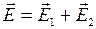 . Напряженности полей, создаваемых в воздухе (e = 1)зарядами q1 и q2:
. Напряженности полей, создаваемых в воздухе (e = 1)зарядами q1 и q2:
E1 = 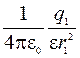 , ( 1 )
, ( 1 )
E2= 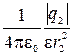 . ( 2 )
. ( 2 )
Направления векторов 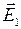 и
и 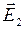 указаны на рис.1. Модуль вектора
указаны на рис.1. Модуль вектора 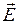 найдем по теореме косинусов:
найдем по теореме косинусов:
E = ( 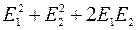 cosa)1/2,
cosa)1/2,
где a – угол между векторами 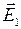 и
и 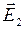 . Из рис. 1 видно, что b=p — a.Тогда cosb = — cosa.
. Из рис. 1 видно, что b=p — a.Тогда cosb = — cosa.
Следовательно,
E = ( 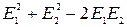 cosb)1/2 . ( 3 )
cosb)1/2 . ( 3 )
Из треугольника со сторонами r1, r2 и d по теореме косинусов находим
cos b = ( r12 r22 — d2)/(2r1r2). ( 4 )
Произведя вычисления по формулам (1), (2), (4), получим:
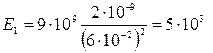 В/м,
В/м,
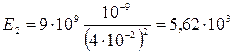 В/м, cosb =
В/м, cosb = 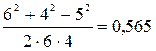 .
.
При вычислении Е2 знак заряда q2 опущен, так как знак минус определяет направление вектора 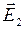 , а направление
, а направление 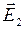 было учтено при его графическом изображении (cм. рис.1).
было учтено при его графическом изображении (cм. рис.1).
Напряженность результирующего поля будет равна
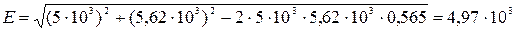 В/м.
В/м.
По принципу суперпозиции потенциал результирующего поля, создаваемого зарядами q1 и q2, равен алгебраической сумме потенциалов j1 и j2, т. е. j = j1 j2 или
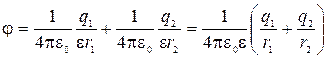 . ( 5 )
. ( 5 )
Произведя вычисления, получим:
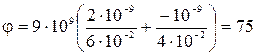 В.
В.
Задача 2
Тонкий прямой стержень длиной 10 см равномерно заряжен с линейной плотностью заряда 1 нКл/см. На продолжении оси стержня, на расстоянии 20 см от ближайшего конца, находится точечный заряд 20 нКл. Определить силу взаимодействия стержня и точечного заряда.
Так как заряженный стержень не является точечным зарядом, то закон Кулона непосредственно применить нельзя. Разобьём стержень на малые элементы и выделим на стержне (рис. 2) элемент 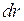 с зарядом
с зарядом 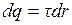 . Этот заряд можно рассматривать как точечный. Тогда по закону Кулона
. Этот заряд можно рассматривать как точечный. Тогда по закону Кулона
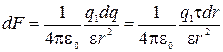 ,
,
Так как силы 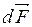 взаимодействия заряда
взаимодействия заряда 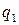 и зарядов
и зарядов 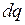 на разных элементах стержня направлены в одну сторону, то геометрическую сумму сил можно заменить алгебраической. Силу взаимодействия точечного заряда и стержня найдём интегрированием выражения (1):
на разных элементах стержня направлены в одну сторону, то геометрическую сумму сил можно заменить алгебраической. Силу взаимодействия точечного заряда и стержня найдём интегрированием выражения (1):
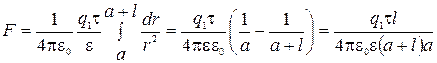 .
.
Проверим, даёт ли расчётная формула единицу силы. Для этого в правую часть формулы вместо символов величин подставим их единицы измерений
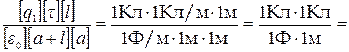
 .
.
Произведем вычисления с учётом того, что 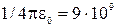 м/Ф:
м/Ф:
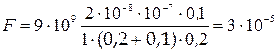 Н.
Н.
Задача 3
Электрическое поле создано длинным цилиндром радиусом 1 см, равномерно заряженным с линейной плотностью заряда 20 нКл/м. Определить работу сил поля по перемещению точечного заряда 25 нКл из точки, находящейся на расстоянии 1 см, в точку, находящуюся на расстоянии 3 см от поверхности цилиндра в средней его части.
Интегрируя это выражение, найдем разность потенциалов между двумя точками, отстоящими на расстояниях r1 и r2 от оси цилиндра,
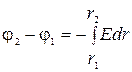 , ( 1 )
, ( 1 )
где r1 = a1 R, r2 = a2 R.
Так как цилиндр длинный и точки взяты вблизи его средней части, то можно воспользоваться формулой напряженности поля, создаваемого бесконечно длинным цилиндром,
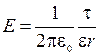 . ( 2 )
. ( 2 )
Подставив (2) в (1), получим:
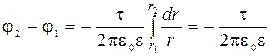 ln
ln 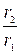
или
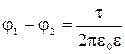 ln
ln 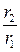 . ( 3 )
. ( 3 )
Таким образом,
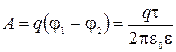 ln
ln 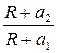 .
.
Проверим, дает ли расчетная формула единицу работы. Для этого в правую часть вместо символов величин подставим их единицы
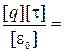
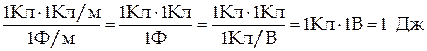
Произведем вычисления с учетом того, что 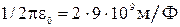 . Так как величины r2 и r1 входят в формулу (3) в виде отношения, их можно выразить в сантиметрах.
. Так как величины r2 и r1 входят в формулу (3) в виде отношения, их можно выразить в сантиметрах.
Таким образом,
А = 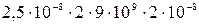 ln
ln =
= 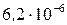 Дж.
Дж.
Задача 4
Электрическое поле создано тонкой бесконечно длинной нитью, равномерно заряженной с линейной плотностью заряда 20 нКл/м. На расстоянии 40 см от нити находится плоская круглая площадка радиусом 1 см. Определить поток вектора напряженности через площадку, если её плоскость составляет угол 30о с линией напряженности, проходящей через середину площадки.
Поле, создаваемое нитью (очень тонким цилиндром), является неоднородным, так как модуль напряженности изменяется от точки к точке:
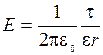 . (1)
. (1)
Поэтому поток вектора 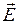 равен
равен
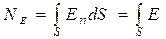 cosadS,
cosadS,
где a – угол между векторами 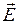 и
и 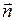 (рис. 3). Так как линейные размеры площадки малы по сравнению с расстоянием до нити (а>>R), то Е в пределах площадки меняется незначительно. Тогда
(рис. 3). Так как линейные размеры площадки малы по сравнению с расстоянием до нити (а>>R), то Е в пределах площадки меняется незначительно. Тогда
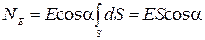 ,
,
где S = pR2 .
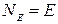 Scosa = EpR2cosa. (2)
Scosa = EpR2cosa. (2)
Из рис. 3 следует, что cosa = cos(p/2— b) = sinb.С учетом этого фор-мула (2) примет вид
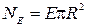 sinb
sinb 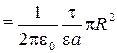 sinb.
sinb.
Произведя вычисления с учетом того, что 1/2pe0= 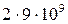 м/Ф, получим:
м/Ф, получим:
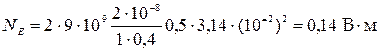
Задача 5
Между пластинами плоского конденсатора, заряженного до разности потенциалов 600 В, находятся два слоя диэлектриков: стекла толщиной 5 мм и эбонита толщиной 3 мм. Площадь каждой пластины 200 см2. Определить: а) напряженность поля, индукцию и падение потенциала в каждом слое; б) электроемкость конденсатора.
Учитывая, что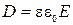 , и сокращая на e0, из равенства (1) получим:
, и сокращая на e0, из равенства (1) получим:
e1E1 = e2Е2, ( 2 )
где Е1и E2 – напряженности поля в первом и во втором слоях диэлектриков; e1 и e2 – диэлектрические проницаемости слоев.
Разность потенциалов между пластинами конденсатора, очевидно, равна сумме напряжений на слоях диэлектриков:
U = U1 U2 . ( 3 )
В пределах каждого слоя поле однородное, поэтому U1= E1d1 и U2= Е2d2. С учетом этого равенство (3) примет вид
U = Е1 d1 E2d2. ( 4 )
Решая совместно уравнения (2) и (4), получим:
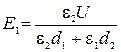 ,
,  .
.
Произведя вычисления, получим:
 ;
;
 ;
;
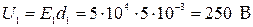 ;
; 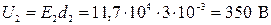 ;
;
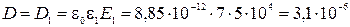 Кл/м2.
Кл/м2.
Определим электроемкость конденсатора
С = q / U, ( 5 )
где q = sS – заряд каждой пластины конденсатора. Учитывая, что поверхностная плотность зарядов s на пластинах конденсатора численно равна модулю электрического смещения, т. е. s = D, получим:
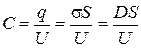 .
.
Проверим, дает ли расчетная формула единицу электроемкости. Для этого в правую часть формулы вместо символов величин подставим их единицы измерений
 .
.
Произведя вычисления, получим:
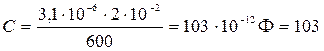 пФ.
пФ.
4.2.2. Постоянный электрический ток
1. Сила и плотность постоянного тока
I=q/t, j=I/S,
где q – заряд, прошедший через поперечное сечение проводника за время t; S – площадь поперечного сечения.
2. Закон Ома
а) 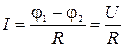 (для участка цепи, не содержащего ЭДС),
(для участка цепи, не содержащего ЭДС),
где I – сила постоянного тока; j1–j2 = U – разность потенциалов на концах участка цепи; R – сопротивление участка цепи;
б)  (для замкнутой цепи),
(для замкнутой цепи),
где 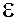 – ЭДС источника тока; R – сопротивление внешней цепи; R0 – внутреннее сопротивление источника тока.
– ЭДС источника тока; R – сопротивление внешней цепи; R0 – внутреннее сопротивление источника тока.
3. Сопротивление R и проводимость G однородного цилиндрического проводника постоянного диаметра
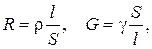
где r – удельное сопротивление проводника; g = 1/r – удельная электропроводность; l – длина проводника; S – площадь поперечного сечения проводника.
4. Работа и мощность тока
A= IUt, P = IU.
5. Закон Джоуля-Ленца
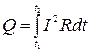 ,
,
для постоянного тока
Q = I2Rt,
где Q – количество теплоты, выделяющейся на участке цепи сопротивлением R за время t, когда по проводнику течет ток силой I.
7. Закон Ома в дифференциальной форме
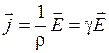 ,
,
где  I/S – плотность тока в проводнике;
I/S – плотность тока в проводнике;  – напряженность электрического поля в проводнике.
– напряженность электрического поля в проводнике.
8. Закон Джоуля-Ленца в дифференциальной форме
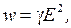
где w= 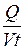 – удельная тепловая мощность тока (количество теплоты, выделяю-щейся в единице объема проводника за единицу времени).
– удельная тепловая мощность тока (количество теплоты, выделяю-щейся в единице объема проводника за единицу времени).
Примеры решения задач
Задача 1
ЭДС батареи аккумуляторов 12 В. Наибольшая сила тока, которую может дать батарея, 5 А. Определить максимальную мощность, которая может выделиться во внешней цепи.
где R0 – внутреннее сопротивление аккумулятора; R – сопротивление внешней цепи (сопротивление нагрузки).
Максимальная сила тока будет при коротком замыкании (R = 0)
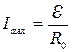 . (2)
. (2)
Из формулы (2) находим внутреннее сопротивление:
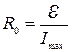 . (3)
. (3)
Мощность, которая выделяется во внешней цепи (полезная мощность),
P=I2R. (4)
C учетом закона Ома (1) получим:
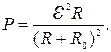 (5)
(5)
Исследуя функцию (5) на максимум, найдем сопротивление нагрузки, при котором мощность максимальна:
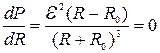 . (6)
. (6)
Из равенства (6) следует, что
R=R0. (7)
Подставив (7) в формулу (5), найдем выражение для максимальной мощности:
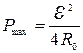 . (8)
. (8)
C учетом формулы (3) получим:
 .
.
Произведя вычисления, получим:
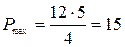 Вт.
Вт.
Задача 2
Сила тока в проводнике сопротивлением 20 Ом равномерно нарастает от 0 до 4 А в течение 2 с. Определить количество теплоты, выделившейся в проводнике за первые полторы секунды.
| Дано: | Решение: |
| R = 20 Ом I1= 0 А, I2= 4А t1 = 0, t2 = 2 c, t3= 1,5 c | Согласно закону Джоуля-Ленца, тепловая мощность, выделяющаяся на сопротивлении R, равна Р = I2R . Количество тепла dQ, выделяющегося за время dt на сопротивлении R, равно |
| Q — ? |
dQ = Pdt = I2Rdt . (1)
По условию задачи сила тока равномерно нарастает, т. е. является линейной функцией времени
I = at b . (2)
В начальный момент t1 = 0 ток I1 равен нулю, поэтому в уравнении (2) имеем b = 0. Таким образом,
I = at . (3)
Коэффициент «а» найдем из условия, что I2 = 4 А при t2= 2 с:
I2 = at2.
Откуда получаем
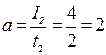 A/c.
A/c.
Подставляя в формулу (1) выражение (3) и интегрируя по времени от 0 до t3, найдем количество выделившегося тепла:
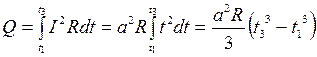 . (4)
. (4)
Подставляя в формулу (4) значения входящих в нее параметров, получим:
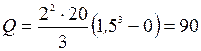 Дж.
Дж.
Магнитостатика
1. Связь магнитной индукции 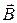 с напряженностью
с напряженностью 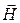 магнитного поля
магнитного поля
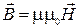 ,
,
где m – относительная магнитная проницаемость изотропной среды (в вакуумеm = 1); m0 – магнитная постоянная (m0 = 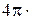 10-7 Гн/м).
10-7 Гн/м).
2. Магнитная индукция в центре кругового витка с током
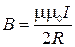 ,
,
где R – радиус кругового витка; I – сила тока.
3. Магнитная индукция поля длинного прямого проводника с током
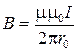 ,
,
где r0 – расстояние от оси проводника до точки, в которой определяется магнитная индукция.
Магнитная индукция поля, создаваемого отрезком провода с током, (рис. 4)
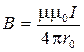 (cosa1— cosa2).
(cosa1— cosa2).
Рис. 4
Обозначения ясны из рисунка. Направление вектора 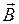 обозначено точкой – это значит, что вектор
обозначено точкой – это значит, что вектор 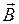 направлен перпендикулярно плоскости рисунка «к нам».
направлен перпендикулярно плоскости рисунка «к нам».
При симметричном расположении концов провода относительно точки, в которой определяется индукция: cosa1= —cosa2 = cosa. Тогда
B = 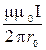 cosa.
cosa.
4. Магнитная индукция поля внутри длинного соленоида с током:
а) в центре соленоида В = mm0In,
б) на краю соленоида В = mm0In/2,
где n = N/l – число витков, приходящееся на единицу длины (N – число витков соленоида, l – длина соленоида).
5. Закон Ампера
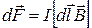 или
или 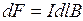 sina,
sina,
где a – угол между направлением тока в элементе проводника и вектором магнитной индукции 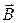 .
.
В случае однородного магнитного поля и прямого отрезка проводника длиной l модуль силы Ампера
F=IBl sina.
6. Сила взаимодействия, приходящаяся на единицу длины каждого из двух длинных прямолинейных параллельных проводов с токами I1 и I2,
F= 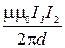 ,
,
где d – расстояние между проводами.
7. Магнитный момент плоского контура с током
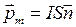 ,
,
где  – единичный вектор нормали к плоскости контура; I – сила тока, протекающего по контуру; S – площадь контура.
– единичный вектор нормали к плоскости контура; I – сила тока, протекающего по контуру; S – площадь контура.
8. Вращающий момент, действующий на контур с током в однородном магнитном поле,
 или
или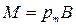 sina,
sina,
где a – угол между векторами 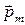 и
и 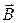 .
.
9. Сила (сила Лоренца), действующая на движущийся заряд в магнитном поле,
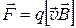 или
или 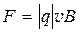 sina,
sina,
где 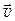 – скорость заряженной частицы; a – угол между векторами
– скорость заряженной частицы; a – угол между векторами 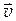 и
и 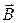 .
.
10. Магнитный поток:
а) через произвольную поверхность S, помещенную в неоднородное поле,
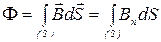 ,
,
где 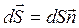 ;
; 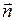 – единичный вектор нормали к элементу поверхности dS;
– единичный вектор нормали к элементу поверхности dS; 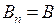 cosa – проекция вектора
cosa – проекция вектора 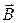 на направление нормали
на направление нормали 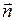 ; a – угол между вектором
; a – угол между вектором 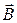 и нормалью
и нормалью 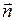 ;
;
б) через плоскую поверхность, помещенную в однородное магнитное поле,
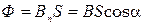 .
.
11. Потокосцепление катушки индуктивности (полный магнитный поток)
 ,
,
где N – число витков катушки; Ф – магнитный поток через один виток.
Формула верна для соленоида и тороида, когда N витков плотно прилегают друг к другу.
12. Работа по перемещению замкнутого контура с током в магнитном поле
А = IDФ = I(Ф2 — Ф1),
где Ф1 и Ф2 – магнитные потоки через контур в начальном и конечном положениях.
Примеры решения задач
Задача 1
По двум бесконечно длинным параллельным проводам текут в одинаковом направлении токи силой 15 и 10 A. Расстояние между проводами 10 см. Определить магнитную индукцию в точке А (рис.5), удаленной от первого провода на расстояние r1 = 10 см и от второго провода на расстояние r2 = 15 см.
Согласно принципу суперпозиции магнитных полей магнитная индукция 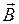 в точке А равна сумме векторов магнитных индукций полей
в точке А равна сумме векторов магнитных индукций полей 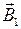 и
и 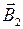 , созданных каждым током в отдельности
, созданных каждым током в отдельности
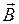 =
= 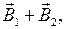 (1)
(1)
где B1=µµ0I1/(2pr1) и B2=µµ0I2/(2pr2). На рис. 5 проводники с токами I1 и I2 перпендикулярны плоскости чертежа (токи направлены от наблюдателя). Векторы 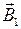 и
и 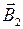 изображены на рисунке так, что их направление связано с направлением соответствующих токов правилом правого винта. Векторы
изображены на рисунке так, что их направление связано с направлением соответствующих токов правилом правого винта. Векторы 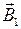 и
и 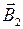 в точке А направлены по касательной к силовым линиям.
в точке А направлены по касательной к силовым линиям.
Модуль вектора 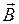 на основании теоремы косинусов равен
на основании теоремы косинусов равен
B= ( 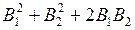 cosa )1/2, (2 )
cosa )1/2, (2 )
где a – угол между векторами 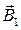 и
и  . Из рис. 5 видно, что углы a и b равны как углы с соответственно перпендикулярными сторонами. Из треугольника со сторонами r1, r2и d по теореме косинусов находим cosa:
. Из рис. 5 видно, что углы a и b равны как углы с соответственно перпендикулярными сторонами. Из треугольника со сторонами r1, r2и d по теореме косинусов находим cosa:
cosa = 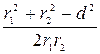 .
.
Вычислим отдельно
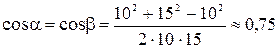
Подставляя выражения для B1 и B2 в формулу (2) и вынося mm0/(2p) за знак корня, получаем
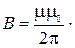
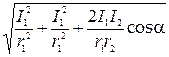 .
.
Произведем вычисления

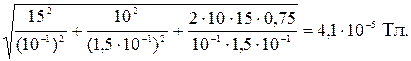
Задача 2
Попроводнику, согнутому в виде прямоугольника со сторонами 8 см и 12 см, течет ток силой 5 А. Определить магнитную индукцию в точке пересечения диагоналей прямоугольника.
Согласно принципу суперпозиции магнитных полей
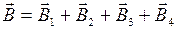 , (1)
, (1)
где B1,B2, B3, B4 – магнитные индукции полей, создаваемых токами, протекающими по каждой стороне прямоугольника (рис. 6).
В точке 0 пересечения диагоналей все векторы индукции 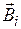 направлены перпендикулярно плоскости прямоугольника. Кроме того, из соображений симметрии следует, что B1 = B3 и B2 = B4 . Поэтому векторное равенство (1) заменим скалярным
направлены перпендикулярно плоскости прямоугольника. Кроме того, из соображений симметрии следует, что B1 = B3 и B2 = B4 . Поэтому векторное равенство (1) заменим скалярным
B = 2B1 2B2, (2)
где B1 и B2 – индукции магнитных полей, создаваемых соответственно токами, текущими по проводникам со сторонами длиной b и а.
Используя формулу для магнитной индукции поля, создаваемого отрезком прямого проводника с током,
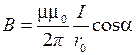 ,
,
получим:
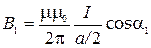 ,
, 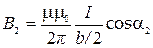 . (3)
. (3)
Из рис. 6 следует, что
 и
и 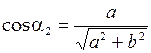 . (4)
. (4)
Подставив формулы (3) и (4) в равенство (2), после алгебраических преобразований получим:
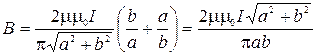 .
.
Проверим, дает ли расчетная формула единицу магнитной индукции. Для этого в правую часть формулы вместо символов величин подставим их единицы измерений:
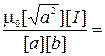
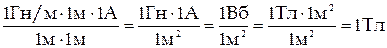 ;
;
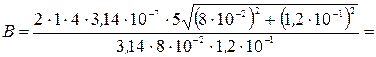
 Тл
Тл 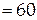 мкТл.
мкТл.
Задача 3
Виток радиусом 3 см, по которому течёт ток силой 5 А, свободно установился в однородном магнитном поле с индукцией 20 мТл. Определить работу, совершаемую внешними силами при повороте витка на угол 90о вокруг оси, совпадающей с диаметром витка. Считать, что при повороте витка сила тока в нем поддерживается постоянной.
В начальном положении согласно условию задачи виток свободно установился в магнитном поле, следовательно, 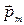 и
и 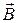 совпадают по направлению, т. е.
совпадают по направлению, т. е. 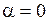 и
и 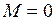 . Чтобы повернуть виток на некоторый угол
. Чтобы повернуть виток на некоторый угол 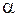 , внешние силы должны совершить работу против момента сил Ампера, так как он стремится возвратить виток в исходное положение. Так как момент сил переменный и зависит от угла поворота
, внешние силы должны совершить работу против момента сил Ампера, так как он стремится возвратить виток в исходное положение. Так как момент сил переменный и зависит от угла поворота 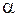 , то
, то
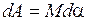 или
или 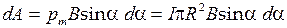 .
.
Взяв интеграл от этого выражения, найдём работу, совершаемую при повороте витка на конечный угол:
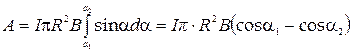 . (1)
. (1)
Так как 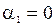 и
и 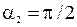 , то
, то
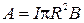 . (2)
. (2)
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
eimax = N2BSw.
Учитывая формулу (2), получим:
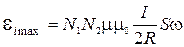 .
.
Произведя вычисления, получим:
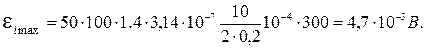
Задача 2
Контур в виде квадрата со стороной 10 см находится в однородном магнитном поле с индукцией 0,5 мТл, причем его плоскость составляет угол 60о c силовыми линиями поля. Какой заряд протечет по контуру при выключении магнитного поля? Сопротивление контура 1 мОм.
При выключении магнитного поля магнитный поток Ф, пронизывающий контур, меняется. В контуре возникает ЭДС индукции, мгновенное значение которой по закону Фарадея равно
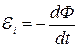 .
.
Мгновенное значение силы индукционного тока определяется по закону Ома
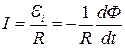 .
.
За время dt по контуру протечет заряд
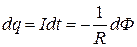 .
.
Проинтегрировав это выражение, найдем полный заряд:
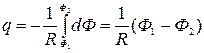 .
.
Для однородного магнитного поля начальный магнитный поток равен
Ф1 = BS cosa,
где a – угол между вектором 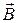 и нормалью к плоскости контура (рис. 8); S = а2 – площадь контура.
и нормалью к плоскости контура (рис. 8); S = а2 – площадь контура.
Из рис. 8 видно, что a = 90о–b. Следовательно, cosa = sinb. Конечный магнитный поток Ф2 = 0.
Таким образом,
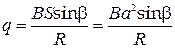 .
.
Произведя вычисления, получим:
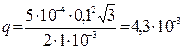 Кл .
Кл .
Проверим, дает ли расчетная формула единицу заряда. Для этого в правую часть формулы вместо символов величин подставим их единицы измерений:
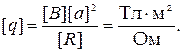 Но из закона Ампера
Но из закона Ампера 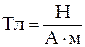 , а из закона Ома
, а из закона Ома 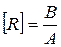 . Таким образом,
. Таким образом, 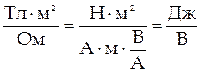 .
.
Из определения потенциала 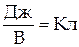 .
.
Задача 3
Соленоид с сердечником из немагнитного материала содержит 1200 витков провода, плотно прилегающих друг к другу. При силе тока 4 А магнитный поток равен 4 мкВб. Определить индуктивность соленоида и энергию его магнитного поля.
В свою очередь, потокосцепление можно найти через поток Ф и число витков N (когда витки плотно прилегают друг к другу):
Y = NФ . ( 2 )
Из формул (1) и (2) находим индуктивность соленоида
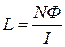 . ( 3 )
. ( 3 )
Энергия магнитного поля соленоида
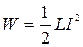 .
.
Выразив L согласно (3), получим:
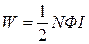 .
.
Подставим в формулы значения физических величин и произведем вычисления
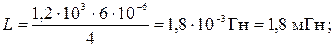
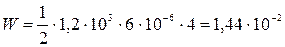 Дж = 14,4 мДж.
Дж = 14,4 мДж.
Проверим размерность для энергии магнитного поля
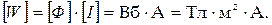
Из выражения для силы Ампера F = 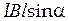 получим:
получим:
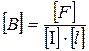 , т. е. Тл =
, т. е. Тл = 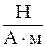 .
.
Таким образом, 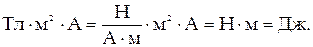
Задание на контрольную работу № 3
301. Три одинаковых точечных заряда 50 нКл находятся в вершинах равностороннего треугольника со стороной 6 см. Найти силу, действующую на один из зарядов со стороны двух остальных.
302. На продолжении оси тонкого прямого стержня, равномерно заряженного с линейной плотностью заряда 400 нКл/см, на расстоянии 30 см от конца стержня, находится точечный заряд 20 мкКл. Второй конец стержня уходит в бесконечность. Определить силу взаимодействия стержня и точечного заряда.
303. Четыре одинаковых точечных заряда 20 нКл закреплены в вершинах квадрата со стороной 10 см. Найти силу, действующую на один из этих зарядов со стороны трех остальных.
304. На продолжении оси тонкого прямого равномерно заряженного стержня длиной 20 см на расстоянии 10 см от его ближайшего конца находится точечный заряд 10 нКл. Определить линейную плотность заряда на стержне, если сила взаимодействия стержня и точечного заряда 6 мкН.
305. Поверхностная плотность заряда бесконечно протяженной верти-кальной плоскости 200 мкКл/м2. К плоскости на нити подвешен заряженный шарик массой 15 г. Определить заряд шарика, если нить образует с плоскостью угол 30о.
306. Две длинные прямые параллельные нити находятся на расстоянии 10 cм друг от друга. На нитях равномерно распределены заряды с линейными плотностями 0,4 и –0,3 нКл/см. Определить напряженность электрического поля в точке, удаленной от первой нити на расстояние 6 см и от второй – на расстояние 8 см.
307. В вершинах правильного шестиугольника со стороной 10 см на-ходятся одинаковые точечные заряды величиной 5 нКл. Найти напряженность и потенциал электростатического поля в центре шестиугольника.
308. Определить напряженность и потенциал электростатического поля, создаваемого зарядом – 3 нКл, равномерно распределенным по тонкому прямому стержню длиной 10 см, в точке, лежащей на продолжении оси стержня на расстоянии 10 см от его конца.
309. Две концентрические металлические заряженные сферы радиусами 5 и 10 см несут соответственно заряды 3 и –1нКл. Найти напряженность и потенциал электростатического поля в точках, лежащих от центра сфер на расстояниях 3, 6 и 12 см. Построить график зависимости напряженности и потенциала от расстояния.
310. Два точечных заряда величиной 1 и –1 нКл находятся на расстоянии 2 см друг от друга. Определить напряженность и потенциал электростатичес-кого поля в точке, удаленной от первого и второго заряда на расстояние 3 см.
311. Электростатическое поле создается двумя бесконечными парал-лельными плоскостями, равномерно заряженными с поверхностными плотностями заряда 0,3 и 0,7 мкКл/м2. Определить напряженность поля между пластинами и вне пластин. Найти разность потенциалов между пластинами, если расстояние между ними 4 см. Построить график изменения напряженности вдоль линии, перпендикулярной пластинам.
312. Решить предыдущую задачу при условии, что заряд второй пластины отрицательный.
313. На расстоянии 2 см от бесконечно длинной равномерно заряженной нити находится точечный заряд 0,4 нКл. Под действием сил поля заряд переместился до расстояния 4 см; при этом совершается работа 0,5 мкДж. Найти линейную плотность заряда нити.
314. Определить работу сил электростатического поля при перемещении точечного заряда –20 нКл из бесконечности в точку, находящуюся на расстоянии 4 см от поверхности сферы радиусом 1 см, равномерно заряженной с поверхностной плотностью заряда 3 нКл/см2.
315. Под действием сил электростатического поля точечный заряд переместился из точки, находящейся на расстоянии 8 см от бесконечно длинной равномерно заряженной нити в точку, находящуюся на расстоянии 2 см; при этом совершается работа 52 мкДж. Найти величину заряда, если линейная плотность заряда нити 50 нКл/см.
316. Протон влетел в однородное электрическое поле с напряженностью 300 В/см в направлении силовых линий со скоростью 100 км/с. Какой путь должен пройти протон, чтобы его скорость удвоилась?
317. В центре сферы радиусом 30 см находится точечный заряд 10 нКл. Определить поток напряженности через часть сферической поверхности площадью 20 см2.
318. Прямоугольная плоская площадка со сторонами 3 и 2 см находится на расстоянии 1 м от точечного заряда 2 мкКл. Площадка ориентирована так, что линии напряженности составляют угол 30о с ее поверхностью. Найти поток напряженности через эту площадку.
319. На некотором расстоянии от бесконечной равномерно заряженной плоскости с поверхностной плотностью заряда 0,5 нКл /см2 расположена круглая пластинка так, что её плоскость составляет угол 30о с силовыми линиями электрического поля. Определить поток напряженности и электрического смещения (индукции) через пластинку, если её радиус 10 см.
320. Бесконечная плоскость, равномерно заряженная с поверхностной плотностью заряда 5 нКл/см2, пересекает сферу по диаметру. Найти поток электрического смещения через сферическую поверхность, если диаметр сферы 4 см.
321. Конденсатор электроёмкостью 0,5 мкФ был заряжен до напряжения 350 В. После того как его соединили параллельно со вторым конденсатором, заряженным до напряжения 500 В, напряжение на нем изменилось до 400 В. Вычислить электроемкость второго конденсатора.
322. Коаксиальный электрический кабель состоит из центральной жилы радиусом 1 см и цилиндрической оболочки радиусом 1,5 см, между которыми находится изоляция. Вывести формулу для емкости такого кабеля и вычислить электроемкость кабеля длиной 10 м, если изоляционным материалом служит резина.
323. Сферический конденсатор состоит из двух тонких концентрических сферических оболочек радиусом 1,5 и 3 см. В пространстве между оболочками находится диэлектрик с диэлектрической проницаемостью 3,2. Вывести формулу для электроёмкости такого конденсатора и вычислить его электроемкость.
324. Определить поверхностную плотность зарядов на пластинах плоского слюдяного конденсатора, заряженного до разности потенциалов 100 В, если расстояние между его пластинами 0,3 мм.
325. Плоский воздушный конденсатор с площадью пластин 100 см2 заряжен до разности потенциалов 300 В. Определить поверхностную плотность заряда на пластинах, электроёмкость и энергию поля конденсатора, если напряженность поля в зазоре между пластинами 60 кВ/м.
326. Плоский слюдяной конденсатор, заряженный до разности потенциалов 600 В, обладает энергией 40 мкДж. Площадь пластин составляет 100 см2. Определить расстояние между пластинами, напряженность и объёмную плотность энергии электрического поля конденсатора.
327. Плоский конденсатор заряжен до разности потенциалов 300 В. Расстояние между пластинами 5 мм, диэлектрик – стекло. Определить напряженность поля в стекле, поверхностную плотность заряда на пластинах и поверхностную плотность связанных поляризационных зарядов на стекле.
328. Пространство между пластинами плоского конденсатора заполнено трансформаторным маслом. Расстояние между пластинами 3 мм. Какое напряжение надо подать на пластины этого конденсатора, чтобы поверхностная плотность связанных поляризационных зарядов на масле была 0,62 нКл/см2?
329. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика: слоем слюды толщиной 0,2 мм и слоем парафинированной бумаги толщиной 0,1 мм. Определить напряженность поля и падение потенциала в каждом из слоев, если разность потенциалов между обкладками конденсатора 220 В.
330. Плоский конденсатор, площадь каждой пластины которого 400 см2, заполнен двумя слоями диэлектрика: слоем парафинированной бумаги толщиной 0,2 см и слоем стекла толщиной 0,3 см. Определить разность потенциалов для каждого слоя и электроёмкость конденсатора, если разность потенциалов между его обкладками 600 В.
331. При каком внешнем сопротивлении потребляемая мощность будет максимальна, если два одинаковых источника с ЭДС 6 В и внутренним сопротивлением 1 Ом каждый соединены последовательно? Чему равна эта мощность?
332. Решить предыдущую задачу для случая, когда источники тока соединены параллельно.
333. ЭДС аккумулятора автомобиля 12 В. При силе тока 3 А его КПД 0,8. Определить внутреннее сопротивление аккумулятора.
334. Два одинаковых источника тока соединены в одном случае последовательно, в другом – параллельно и замкнуты на внешнее сопротивление 1 Ом. При каком внутреннем сопротивлении источника тока сила тока во внешней цепи будет в обоих случаях одинакова?
335. В проводнике за время 10 с при равномерном возрастании силы тока от 0 до 2 А выделилось количество теплоты 6 кДж. Найти сопротивление проводника.
336. При замыкании аккумуляторной батареи на резистор сопротив-лением 9 Ом в цепи идет ток силой 1 А. Сила тока короткого замыкания равна 10 А. Какую наибольшую полезную мощность может дать батарея?
337. Сила тока в проводнике равномерно увеличивается от нуля до некоторого максимального значения за 20 с. За это время в проводнике выделилось количество теплоты 4 кДж. Определить скорость нарастания тока в проводнике, если его сопротивление 6 Ом.
338. По алюминиевому проводу сечением 0,2 мм2 течет ток силой 0,3 А. Определить силу, действующую на отдельные свободные электроны со стороны электрического поля.
339. В медном проводнике площадью поперечного сечения 4 мм2 и длиной 6 м ежеминутно выделяется количество теплоты 18 Дж. Вычислить напряженность электрического поля, плотность и силу электрического тока в проводнике.
340. Сила тока в проводнике сопротивлением 8 Ом за время 10 секунд равномерно возрастает от нуля до 12 А. Определить количество теплоты, выделившейся за это время в проводнике.
341. Бесконечно длинный провод образует круговой виток, касательный к проводу, по проводу идет ток силой 3 А. Найти радиус витка, если напряженность магнитного поля в центре витка 20 А/м.
342. По двум одинаковым круговым виткам радиусом 6 см, плоскости которых взаимно перпендикулярны, а центры совпадают, текут одинаковые токи силой 3 А. Найти напряженность и индукцию магнитного поля в центре витков.
343. По двум бесконечно длинным параллельным проводам, находя-щимся на расстоянии 10 см друг от друга в воздухе, текут в одном направлении токи силой 20 и 30 А. Определить индукцию магнитного поля в точке, лежащей на прямой, соединяющей оба провода, и находящейся на расстоянии 2 см от первого провода.
344. Решить предыдущую задачу при условии, что токи в проводниках текут в противоположных направлениях.
345. По двум длинным параллельным проводам, находящимся на расстоянии 4 см в воздухе, текут в одном направлении одинаковые токи силой 5 А. Определить индукцию и напряженность магнитного поля в точке, удаленной от каждого провода на расстояние 4 см.
346. Определить индукцию и напряженность магнитного поля в центре проволочной квадратной рамки со стороной 8 см, если по рамке проходит ток силой 3 А.
347. По двум тонким длинным параллельным проводам, расстояние между которыми 10 см, текут в одном направлении токи силой 3 и 2 А. Определить индукцию и напряженность магнитного поля в точке, удаленной на расстояние 6 см от первого провода и на расстояние 8 см от второго провода, если провода находятся в воздухе.
348. Бесконечно длинный прямой проводник согнут под прямым углом. По проводнику течет ток силой 2 А. Найти напряженность и магнитную индукцию в точке, расположенной на биссектрисе угла на расстоянии 5 см от сторон проводника.
349. По проводу, согнутому в виде правильного шестиугольника с длиной стороны 10 см, течет ток силой 5 А. Найти напряженность и магнитную индукцию в центре шестиугольника.
350. Два бесконечно длинных провода скрещены под прямым углом. Расстояние между проводами равно 10 см. По проводам текут одинаковые токи силой 10 А. Найти индукцию и напряженность магнитного поля в точке, находящейся на середине расстояния между проводами.
351. Прямой провод согнут в виде квадрата со стороной 8 см. Какой силы ток надо пропустить по проводнику, чтобы напряженность магнитного поля в точке пересечения диагоналей была 20 А/м?
352. Сила взаимодействия двух параллельных проводов, по которым текут одинаковые токи, равна 1 мН. Найти силу тока в проводах, если расстояние между ними 1 см, а длина каждого провода 1 м.
353. В однородном магнитном поле с индукцией 20 мТл находится прямоугольная рамка длиной 6 см и шириной 2 см, содержащая 100 витков проволоки. Сила тока в рамке 1 А, а плоскость рамки параллельна линиям магнитной индукции. Определить магнитный момент рамки и механический вращающий момент, действующий на рамку.
354. Каким образом надо расположить прямой алюминиевый проводник в однородном горизонтальном магнитном поле с индукцией 50 мТл и какой силы ток надо пропустить по нему, чтобы он находился в равновесии? Плотность алюминия 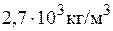 , а радиус проводника 1 мм.
, а радиус проводника 1 мм.
355. Контур из провода, изогнутый в виде квадрата со стороной 5 см, расположен в одной плоскости с бесконечным прямолинейным проводом с силой тока 4 А так, что его две стороны параллельны проводу. Сила тока в контуре 0,2 А. Определить силу, действующую на контур, если ближайшая к проводу сторона контура находится на расстоянии 5 см.
356. Незакрепленный прямой проводник массой 1 г и длиной 8 см, по которому течет ток, находится в равновесии в горизонтальном однородном магнитном поле с напряженностью 100 кА/м. Определить силу тока в проводнике, если он перпендикулярен линиям индукции поля.
357. Проволочный виток радиусом 10 см, по которому течет ток силой 2 А, величина которого поддерживается неизменной, свободно установился в однородном магнитном поле. При повороте витка относительно оси, совпадающей с диаметром, на угол 600 была совершена работа 20 мкДж. Найти напряженность магнитного поля.
358. Проводник, согнутый в виде квадрата со стороной 8 см, лежит на столе. Квадрат, потянув за противоположные вершины, вытянули в линию. Определить совершенную при этом работу. Сила тока 0,5 А в проводнике поддерживается неизменной. Вертикальная составляющая напряженности магнитного поля Земли 40 А/м.
359. Проволочное кольцо радиусом 10 см, по которому течет ток силой 1 А, свободно установилось в однородном магнитном поле с индукцией 0,04 Тл. При повороте контура относительно оси, лежащей в плоскости кольца, на некоторый угол была совершена работа 0,157 мДж. Найти угол поворота контура. Считать, что сила тока в контуре поддерживается неизменной.
360. Проволочное кольцо радиусом 5 см лежит на столе. По кольцу течет ток силой 0,2 А. Поддерживая силу тока неизменной, кольцо перевернули с одной стороны на другую. Какая работа была совершена при этом? Вертикальную составляющую напряженности магнитного поля Земли принять равной 40 А/м.
361. В однородном магнитном поле с индукцией 20 мТл равномерно движется прямой проводник длиной 25 см, по которому течет ток силой 0,3 А. Скорость проводника 15 см/с и направлена перпендикулярно силовым линиям поля. Найти работу перемещения проводника за 5 с и мощность, затраченную на перемещение.
362. Протон и электрон, ускоренные одинаковой разностью потенциалов, влетают в однородное магнитное поле. Во сколько раз радиус кривизны траектории протона больше радиуса кривизны траектории электрона?
363. Протон и электрон, двигаясь с одинаковыми скоростями, влетают в однородное магнитное поле перпендикулярно линиям индукции. Во сколько раз радиус кривизны траектории протона больше радиуса кривизны траектории электрона?
364. Электрон, ускоренный электрическим полем с разностью потенциалов 300 В, влетает перпендикулярно силовым линиям в однородное магнитное поле и движется по окружности радиусом 10 см. Определить индукцию магнитного поля и период обращения электрона по окружности.
365. Электрон, двигаясь со скоростью 4 Мм/с, влетает под углом 60о к силовым линиям однородного магнитного поля с индукцией 1 мТл. Определить радиус и шаг винтовой линии, по которой будет двигаться электрон в магнитном поле.
366. В однородное магнитное поле с индукцией 0,1Тл влетает перпен-дикулярно силовым линиям 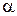 — частица с кинетической энергией 400 эВ. Найти силу, действующую на
— частица с кинетической энергией 400 эВ. Найти силу, действующую на 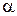 — частицу, радиус окружности, по которой движется
— частицу, радиус окружности, по которой движется 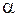 — частица, и период обращения
— частица, и период обращения 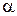 — частицы.
— частицы.
367. Протон влетает в однородное магнитное поле под углом 60о к силовым линиям и движется по винтовой линии, радиус которой 1,5 см, индукция магнитного поля 10 мТл. Найти кинетическую энергию протона.
368. Перпендикулярно магнитному полю с индукцией 0,02 Тл возбуждено электрическое поле с напряженностью 20 кВ/м. Перпендикулярно обоим полям прямолинейно движется заряженная частица. Определить скорость частицы.
369. В однородном магнитном поле с индукцией 0,2 Тл движется протон. Траектория его движения представляет винтовую линию с радиусом 10 см и шагом 60 см. Определить скорость протона.
370. В однородном магнитном поле перпендикулярно линиям магнитной индукции движется прямой проводник длиной 60 см. Определить силу Лоренца, действующую на свободный электрон в проводнике, если на его концах возникает разность потенциалов 20 мкВ.
371. Индукция магнитного поля между полюсами двухполюсного генератора 0,8 Тл. Ротор имеет 100 витков площадью 400 см2. Определить частоту вращения ротора, если максимальное значение ЭДС индукции 200 B .
372. В однородном магнитном поле с индукцией 10 мТл равномерно с частотой 5 оборотов в секунду вращается стержень длиной 40 см так, что плоскость его вращения перпендикулярна линиям индукции магнитного поля, а ось вращения проходит через один из его концов. Определить индуцируемую на концах стержня разность потенциалов.
373. Какой силы ток течет через гальванометр, присоединенный к железнодорожным рельсам, расстояние между которыми 152 см, когда к нему со скоростью 72 км/ч приближается поезд? Вертикальную составляющую индукции магнитного поля Земли принять равной 50 мкТл; сопротивление гальванометра 50 Ом.
374. Катушка из 100 витков площадью 15 см2 вращается в однородном магнитном поле с частотой 5 оборотов в секунду. Ось вращения перпендикулярна оси катушки и силовым линиям поля. Определить индукцию магнитного поля, если максимальное значение ЭДС индукции, возникающей в катушке, равно 0,25 В.
375. В проволочное кольцо, присоединенное к баллистическому галь-ванометру, вставили прямой магнит. При этом по цепи прошел заряд 50 мкКл. Определить изменение магнитного потока через кольцо, если сопротивление цепи гальванометра 10 Ом.
376. Тонкий провод сопротивлением 0,2 Ом согнут в виде квадрата со стороной 10 см и концы его замкнуты. Квадрат помещен в однородное магнитное поле с индукцией 4 мТл так, что его плоскость перпендикулярна силовым линиям поля. Определить заряд, который протечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию.
377. Рамка из провода сопротивлением 0,06 Ом равномерно вращается в однородном магнитном поле с индукцией 4 мТл. Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Площадь рамки 100 см2. Определить заряд, который потечет по рамке при изменении угла между нормалью к рамке и линиями индукции: 1) от 0 до 45о; 2) от 45о до 90о.
378. Сила тока в соленоиде равномерно возрастает от 0 до 5 А за 10 с, при этом в соленоиде возникает магнитное поле с энергией 100 мДж. Определить среднюю ЭДС самоиндукции, возникающую в соленоиде.
379. Соленоид длиной 30 см и площадью поперечного сечения 10 см2 с сердечником из немагнитного материала (m = 1) содержит 600 витков. Определить индуктивность соленоида и среднее значение ЭДС самоиндукции, возникающей при выключении тока в соленоиде, если сила тока уменьшается от 0,8 А до 0 за время 150 мкс.
380. Соленоид сечением 20 см2 и длиной 40 см с сердечником из немагнитного материала (m = 1) содержит 800 витков. Найти индуктивность соленоида, полный магнитный поток, сцепленный с соленоидом, и энергию магнитного поля, если по виткам течет ток силой 2 А.
5. КОНТРОЛЬНАЯ РАБОТА № 4 “КОЛЕБАНИЯ И ВОЛНЫ”
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
В контрольную работу 4 включены задачи по темам: механические колебания, электромагнитные колебания, упругие и электромагнитные волны, интерференция, дифракция, поляризация света.
При решении задач следует выполнить общие методические рекомендации.
Задачи 401…410 относятся к теме «Механические гармонические колебания». Для решения этих задач необходимо изучить тему «Механические колебания» по учебному пособию [1], с. 255…261.
Рекомендуется учитывать, что колебания различной физической природы описываются математически одинаково. Различные характеристики колебаний можно получить из уравнений колебаний, применяя дифференцирование или интегрирование. Обращать внимание на фазовые сдвиги между различными характеристиками, например, между смещением и скоростью, ускорением; или между током и напряжением.
Задачи 411…420 относятся к теме “Затухающие механические колебания”. Приступая к решению этих задач, необходимо ознакомиться с данной темой по учебному пособию [1], с. 267…276.
Следует обращать внимание на физический смысл коэффициента затухания, логарифмического декремента затухания, на связь между частотой затухающих колебаний и собственной частотой.
Задачи 421…430 относятся к теме «Электромагнитные колебания». Приступая к решению этих задач, необходимо ознакомиться с данной темой по учебному пособию [1], с. 261…263, 267…283. Решение этих задач предполагает, что закономерности механических и электрических колебаний математически выражаются одинаково.
Задачи 431…440 относятся к теме “Сложение колебаний”.
Для решения этих задач необходимо ознакомиться с конкретными физическими понятиями, законами или формулами данной темы по учебному пособию [1], с. 261…263, 267…283.
При решении задач на сложение колебаний обращать внимание на разность фаз складываемых колебаний.
Задачи 441…450 относятся к теме “Упругие и электромагнитные волны”. Приступая к решению этих задач, необходимо ознакомиться с данной темой по учебному пособию [1], с. 284…289, 297…305.
Иметь в виду, что уравнения упругих и электромагнитных волн математически одинаковы, их можно использовать так же, как уравнения колебаний.
Задачи 451…460 относятся к теме «Интерференция света”. Теоретический материал по этой теме изложен в [1], с. 316…331.
Задачи 461…470 относятся к теме “Дифракция света”. Для решения этих задач следует ознакомиться с конкретными физическими понятиями, законами или формулами данной темы по учебному пособию [1], с. 332…347.
Задачи 471…480 относятся к теме “Поляризация света”. Приступая к решению этих задач, необходимо ознакомиться с данной темой по учебному пособию [1], с. 355…366 и 351…353.
При решении задач на волновые свойства света (интерференция, дифракция, поляризация, поглощение) помнить, что за световой вектор принимается вектор напряжённости электрического поля; все энергетические характеристики света аналогичны таковым для электромагнитных волн.
Табл. 4
5.2. Основные законы и формулы. Примеры решения задач
Гармонические механические колебания
1) Кинематическое уравнение гармонических колебаний материальной точки
x = Acos(wt j),
где x – смещение от положения равновесия; A – амплитуда колебаний; (wt j) – фаза; j – начальная фаза; w – круговая частота.
2) Скорость и ускорение материальной точки, совершающей гармонические колебания
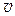 = — A wsin(wt j),
= — A wsin(wt j),
a = — A w2cos(wt j).
3) Период колебаний
а) тела, подвешенного на пружине,
T = 2p 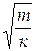 ,
,
где m – масса тела; к – жесткость пружины;
b) математического маятника
T = 2p 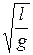 ,
,
где l – длина маятника; g – ускорение свободного падения;
c) физического маятника
T = 2p 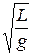 = 2p
= 2p 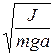 ,
,
где J – момент инерции колеблющегося тела относительно оси колебаний; а – расстояние от центра тяжести маятника до оси колебаний; L = J/ma – приведенная длина физического маятника.
Примеры решения задач
Задача 1
К невесомой пружине, коэффициент упругости которой 200 Н/м, прикреплен груз массой 1 кг. Груз смещен на 10 см от положения равновесия, после чего предоставлен себе. Определить наибольшее и наименьшее ускорения груза. Трением пренебречь.
где 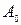 – амплитуда колебания; w – циклическая частота.
– амплитуда колебания; w – циклическая частота.
Продифференцировав выражение (1) по времени, определим скорость груза:
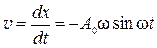 , (2) а после дифференцирования скорости по времени – ускорение
, (2) а после дифференцирования скорости по времени – ускорение
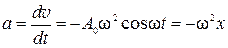 . (3)
. (3)
Так как 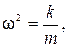 то ускорение а можно записать в виде
то ускорение а можно записать в виде
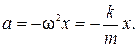 (4)
(4)
Ускорение имеет максимальное значение при 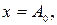 то есть при наибольшем отклонении от положения равновесия
то есть при наибольшем отклонении от положения равновесия
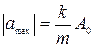 . (5)
. (5)
В положении равновесия, при x = 0, ускорение a = 0. Подставляя числовые значения в выражение (5), получим:
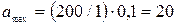 м/с2.
м/с2.
5.2.2. Затухающие колебания
1) Уравнение затухающих колебаний
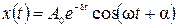 ,
,
где 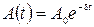 – амплитуда затухающих колебаний;
– амплитуда затухающих колебаний; 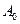 – начальная амплитуда (при t = 0);
– начальная амплитуда (при t = 0); 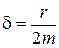 – коэффициент затухания;
– коэффициент затухания; 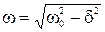 – круговая частота.
– круговая частота.
2) Логарифмический декремент затухания
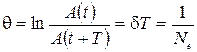 ,
,
где T – период колебаний;  количество колебаний, совершаемых за время уменьшения амплитуды в e раз.
количество колебаний, совершаемых за время уменьшения амплитуды в e раз.
3) Добротность колебательной системы при  :
:
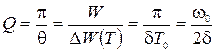 ,
,
где  – полная энергия системы;
– полная энергия системы;  – потери энергии за период.
– потери энергии за период.
Примеры решения задач
Задача 1
Прибор для измерения плотности жидкостей – ареометр массой 0,8 кг с цилиндрической трубкой диаметром 0,3 см опущен в жидкость плотностью 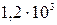 кг/м3. Ареометр получил небольшой импульс в вертикальном направлении и опустился на глубину
кг/м3. Ареометр получил небольшой импульс в вертикальном направлении и опустился на глубину 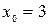 см. Коэффициент сопротивления
см. Коэффициент сопротивления 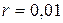 кг/с. Определить: циклическую частоту колебаний; количество колебаний, через которое амплитуда уменьшится в 3 раза.
кг/с. Определить: циклическую частоту колебаний; количество колебаний, через которое амплитуда уменьшится в 3 раза.
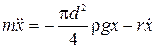
преобразуется в уравнение колебаний
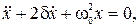
где 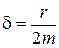 – коэффициент затухания;
– коэффициент затухания; 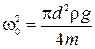 – собственная частота колебаний.
– собственная частота колебаний.
Частота затухающих колебаний

Подставляя числовые значения, получим: 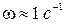
Амплитуда затухающих колебаний
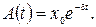
При уменьшении амплитуды в 3 раза
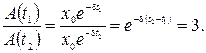
Отсюда 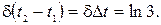
Учитывая, что 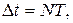 а
а 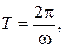 получим:
получим:
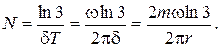
Подставляя числовые значения, получим: 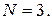
5.2.3. Электромагнтные колебания
1) Эффективные (действующие) значения напряжения и силы переменного тока
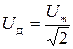 ,
, 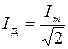 ,
,
где Um и Im – амплитудные значения напряжения и силы тока.
2) Закон Ома для цепи переменного тока, содержащей последовательно соединенные резистор сопротивлением R, катушку индуктивностью L и конденсатор электроемкостью С
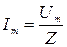 или
или 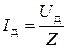 ,
,
где Z = 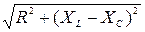 – полное сопротивление цепи;
– полное сопротивление цепи; – индуктивное сопротивление;
– индуктивное сопротивление; 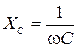 – емкостное сопротивление;
– емкостное сопротивление;  – круговая частота переменного тока.
– круговая частота переменного тока.
При этом сдвиг фаз между напряжением и силой тока определяется из условия
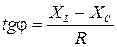 или
или 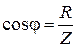 .
.
3) Средняя мощность, выделяемая в цепи переменного тока,
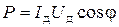 ,
,
где j – сдвиг фаз между напряжением и силой тока.
4) Период собственных электромагнитных колебаний в контуре без активного сопротивления (формула Томсона)
T = 2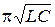 ,
,
где L – индуктивность контура; С – электроемкость.
Примеры решения задач
Задача 1.
Разность потенциалов между обкладками конденсатора электроемкостью 0,5 мкФ в колебательном контуре изменяется со временем по закону U = 100sin1000pt B. Определить период собственных колебаний, индуктивность, полную энергию контура и максимальную силу тока, текущего по катушке индуктивности. Активным сопротивлением контура пренебречь.
напряжения на обкладках конденсатора; w – собственная круговая частота колебаний, которая связана с периодом соотношением T=2p/w. Отсюда находим
Т = 2π/1000π = 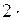 10-3 с.
10-3 с.
Период собственных колебаний в контуре определяется по формуле Томсона T = 2p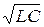 , откуда
, откуда
L = 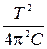 ; L =
; L = 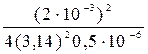 = 0,2 Гн.
= 0,2 Гн.
Полная энергия контура складывается из энергии электрического поля WC конденсатора и энергии магнитного поля WL катушки:
W = WC WL = 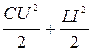 .
.
Полная энергия электрического контура равна максимальной энергии поля конденсатора WCmax = 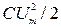 или максимальной энергии поля катушки WLmax =
или максимальной энергии поля катушки WLmax = 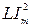 /2.
/2.
Таким образом,
W = 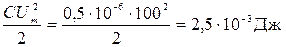 .
.
Зная полную энергию, можно определить максимальную силу тока, протекающего по катушке индуктивности:
Im =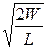 ; Im =
; Im =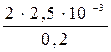 = 0,16 A.
= 0,16 A.
5.2.4. Сложение гармонических колебаний
1) Сложение гармонических колебаний одного направления и одинаковой частоты:
— амплитуда результирующего колебания
A = 
— начальная фаза результирующего колебания
j = arctg .
.
2) Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях (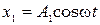 , y =
, y = 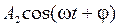 ):
):
а) 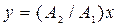
 (если разность фаз
(если разность фаз 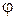 = 0);
= 0);
б) 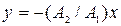 (если разность фаз
(если разность фаз  =
= 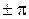 );
);
в) 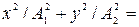 1(если разность фаз
1(если разность фаз 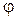 =
= 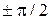 ).
).
Примеры решения задач
Задача 1
Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых:
x= A1cos 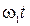 ,(1)
,(1)
y = A2cos 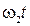 , (2)
, (2)
где А1 = 1 см; 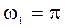 с—1; А2 = 2 см;
с—1; А2 = 2 см;  с-1.
с-1.
Найти уравнение траектории точки. Построить траекторию с соблюдением масштаба и указать направление движения точки.
Используя это соотношение и отбросив размерности x и y,можно написать:
y = 2 cos 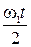 = 2
= 2 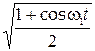 ; х = cos
; х = cos 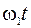 ,
,
откуда
y = 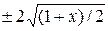 или y =
или y = 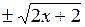 . (3)
. (3)
Выражение (3) есть уравнение параболы, ось которой совпадает с осью ОХ. Как показывают уравнения (1) и (2), амплитуда колебаний точки по оси OX равна 1, а по оси ОУ –2. Следовательно, абсциссы всех точек траектории заключены в пределах от –1 до 1, а ординаты – от –2 до 2.
Для построения траектории найдем из уравнения (3) значения y, соответствующие ряду значений x, удовлетворяющих условию 
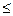 1:
1:
x y = 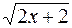 х y =
х y = 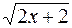
— 1 0 0 ± 1,41
— 0,75 ± 0,71 0,5 ± 1,73
— 0,5 ± 1  1 ± 2
1 ± 2
1 x
-1
Рис. 1
Начертив координатные оси и выбрав единицу длины (сантиметр), построим точки. Соединив их плавной кривой, получим траекторию результирующего колебания точки, которая представляет собой часть параболы, заключенной внутри прямоугольника амплитуд.
Далее определим направление движения точки. Из уравнений (1) и (2) находим, что период колебаний точки по горизонтальной оси Тх = 2с, а по вертикальной оси Ту = 4 с.
Следовательно, когда точка совершает одно полное колебание по оси ОХ, она совершает только половину полного колебания по оси OУ. В начальный момент (t = 0) имеем: х = 1, у = 2 (точка находится в положении 1) при t = 1 с получим: х = –1 и у = 0 (точка находится в вершине параболы); При t = 2 с получим: х = 1 и у = –2 (точка находится в положении 2). После этого она будет двигаться в обратном направлении.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
1) Уравнение плоской бегущей волны
y = A cos (t – x/
(t – x/  ),
),
где y – смещение любой из точек среды с координатой x в момент t; 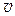 – скорость распространения колебаний в среде.
– скорость распространения колебаний в среде.
2) Связь разности фаз Dj колебаний с расстоянием между точками среды, отсчитанным в направлении распространения колебаний,
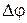 = (2
= (2  /
/ 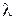 )
) 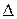 x,
x,
где l – длина волны.
3) Фазовая скорость распространения электромагнитных волн в среде
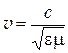 ,
,
где с – скорость электромагнитных волн в вакууме, с = 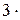 108 м/c.
108 м/c.
4) Связь длины электромагнитной волны с периодом Т и частотой  колебаний
колебаний
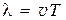 или
или 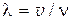 .
.
5) В плоской электромагнитной волне
E 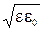 =
=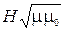 .
.
6) Вектор Пойнтинга
П = [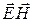 ].
].
Модуль вектора Пойнтинга равен плотности потока энергии электромагнитной волны.
Примеры решения задач
Задача 1
Плоская волна распространяется в упругой среде со скоростью 100 м/с. Наименьшее расстояние между точками среды, фазы колебаний которых противоположны, равно 1м. Определить период колебаний и частоту.
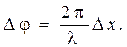 (1)
(1)
Решая это равенство относительно l, получаем
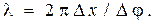 (2)
(2)
По условию задачи Dj = p. Подставляя значения величин, входящих в выражение (2), получим:
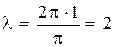 м.
м.
Скорость 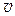 распространения волны связана с l и Т отношением
распространения волны связана с l и Т отношением
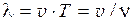 , (3)
, (3)
где 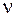 – частота колебаний.
– частота колебаний.
Из выражения (3) получаем 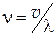 .
.
Произведем вычисления:
 = (100 / 2) = 50 Гц, Т = 1/50 с = 0,02 с.
= (100 / 2) = 50 Гц, Т = 1/50 с = 0,02 с.
5.2.6. Интерференция света
1) Скорость света в среде
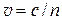 ,
,
где с – скорость света в вакууме; n – показатель преломления среды.
2) Оптическая длина пути световой волны
L = nl,
где l – геометрическая длина пути световой волны в среде с показателем преломления n.
3) Оптическая разность хода двух световых волн
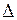 = L1– L2 .
= L1– L2 .
4) Связь разности фаз колебаний 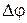 с оптической разностью хода
с оптической разностью хода
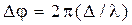 ,
,
где l – длина световой волны в вакууме.
5) Условие максимального усиления света при интерференции
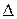 =
= 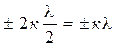 , к = 0, 1, 2…
, к = 0, 1, 2…
Условие максимального ослабления света при интерференции
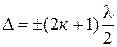 .
.
6) Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки:
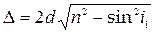 —
— 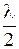 =
= 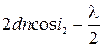 ,
,
где d – толщина пленки; n – показатель преломления пленки; i1 – угол падения; i2 – угол преломления света в пленке.
Разность хода – l/2 возникает при отражении света от оптически более плотной среды.
7) Радиус светлых колец Ньютона в отраженном свете
r 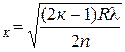 , к = 1, 2, 3…,
, к = 1, 2, 3…,
где к – номер кольца; R – радиус кривизны; n – показатель преломления среды, находящейся между линзой и стеклянной пластинкой.
Радиус темных колец Ньютона в отраженном свете
r 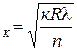 , к = 0, 1, 2…
, к = 0, 1, 2…
Примеры решения задач
Задача 1
Расстояние между двумя когерентными источниками равно 0,9 мм. Источники, испускающие монохроматический свет с длиной волны 640 нм, расположены на расстоянии 3,5 м от экрана. Определить число светлых полос, которые наблюдаются на 1 см длины экрана.
D= S2 – S1 = кl, (1)
где S2, S1 – оптические пути интерферирующих волн;l – длина волны падающего света; к – номер светлой полосы (центральная светлая полоса принята за нулевую). Оптическая разность хода волн D = xd/L, где x – расстояние от центральной светлой полосы до к-й светлой полосы.

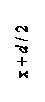
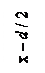
 Ок
Ок
S1
SI О1 O1
О
d S2
SII O2
L
Рис. 10
Учитывая выражение (1), получим:
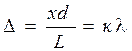 . (2)
. (2)
Из выражения (2) определяем искомую величину 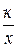 – число светлых интерференционных полос на 1 см длины:
– число светлых интерференционных полос на 1 см длины:
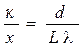 .
.
Подставим в это выражение числовые значения и получим:
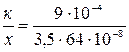 = 400 м-1 ,
= 400 м-1 ,
откуда 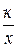 на 1 см равно 4.
на 1 см равно 4.
Задача 2
Для устранения отражения света от поверхности линзы на нее наносится тонкая пленка вещества с показателем преломления(n = 1,26), меньшим, чем у стекла (просветление оптики). При какой наименьшей толщине пленки отражение света с длиной волны 0,55 мкм не будет наблюдаться, если угол падения лучей 30о?
Оптическая разность хода лучей, отраженных от верхней и нижней поверхностей пленки (рис. 3), равна
D = 2d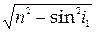 , (1)
, (1)
где d – толщина пленки; n – показатель преломления пленки; i1 – угол падения лучей.
В выражении (1) учтено, что отражение лучей на верхней и нижней поверхностях пленки происходит от оптически более плотной среды и поэтому потери полуволны в обоих случаях компенсируют друг друга.
Условие интерференционного минимума
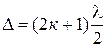 . (2)
. (2)
Из (1) и (2) находим
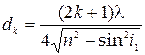 . (3)
. (3)
Полагая к = 0, 1, 2, 3…., получим ряд возможных значений толщины пленки. Минимальная толщина пленки будет при к = 0.
Подставим в расчетную формулу (3) числовые значения входящих величин: n = 1,26; l = 0,55 мкм = 5,5 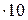 -7 м; i1 = 30о; к = 0.
-7 м; i1 = 30о; к = 0.
Произведем вычисления:
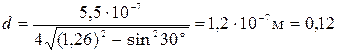 мкм.
мкм.
5.2.7. Дифракция света
1) Радиус к-й зоны Френеля:
— для сферической волны
r 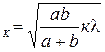 ,
,
где a – расстояние между диафрагмой с круглым отверстием и точечным источником света; b – расстояние между диафрагмой и экраном, на котором ведется наблюдение дифракционной картины; к – номер зоны Френеля; l – длина волны.
— для плоской волны
r 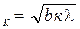 .
.
2) Дифракция света на одной щели при нормальном падении света (дифракция Фраунгофера).
Угол j отклонения лучей, соответствующих минимуму интенсивности света, определяется из условия
asin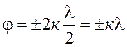 , к = 0, 1, 2 …,
, к = 0, 1, 2 …,
где a – ширина щели; к – порядковый номер минимума; l – длина волны.
Угол j отклонения лучей, соответствующий максимуму интенсивности света, определяется из условия
asin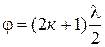 , к = 0, 1, 2 …,
, к = 0, 1, 2 …,
где j – приближенное значение угла дифракции.
3) Дифракция света на дифракционной решетке при нормальном падении лучей.
Условие главных максимумов интенсивности
d sin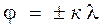 , к = 0, 1, 2 …,
, к = 0, 1, 2 …,
где d – период (постоянная решетки); к – номер главного дифракционного максимума в случае монохроматического света или порядок спектра в случае белого света; j – угол отклонения лучей, соответствующий максимуму интенсивности.
4) Разрешающая способность дифракционной решетки
R =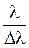 = к N,
= к N,
где Dl – наименьшая разность длин волн двух соседних спектральных линий (l и l Dl), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; N – число щелей решетки.
5) Формула Вульфа-Брэггов
2dsin ,
,
где q – угол скольжения (угол между направлением параллельного пучка рентгеновского излучения, падающего на кристалл, и атомной плоскостью в кристалле); d – расстояние между атомными плоскостями кристалла.
Примеры решения задач
Задача 1
На дифракционную решетку длиной 10 мм, имеющую 400 штрихов на 1 мм, падает нормально свет от разрядной трубки. Помещенная вблизи решетки линза проецирует дифракционную картину (рис. 4) на плоский экран Э, удаленный от линзы на расстояние 1м. Определить: 1) ширину спектра первого порядка, если границы видимого спектра составляют 780 нм (красный край спектра) и 400 нм (фиолетовый край спектра); 2) число спектральных линий красного цвета, которые теоретически можно наблюдать с помощью данной дифракционной решетки; 3) в спектре какого порядка эта решетка может разрешить две линии с длиной волны, равной 500 нм и 500,1 нм?
Аналогично для дифракционного максимума красного цвета получим:
sin 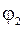 =
=  . (3)
. (3)
Из рис. 4 следует, что расстояние от центра дифракционной картины до фиолетовой спектральной линии равно
l1 = Ltg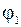 , (4)
, (4)
соответственно для красной спектральной линии
l2 = L tg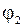 . (5)
. (5)
l0
линза

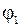 L
L
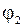
Э
l1
l2
Рис. 4
Ширина спектра первого порядка будет Δl = l2 – l1 или с учетом формул (4) и (5)
Δl = L (tg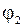 –tg
–tg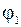 ). (6)
). (6)
В случае малых углов  , что имеет место для спектра первого порядка
, что имеет место для спектра первого порядка
tg
 sin
sin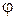 .
.
Поэтому, подставив выражения (2) и (3) в формулу (6), получим:
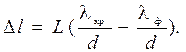 (7)
(7)
Зная число штрихов n на 1 мм решетки, найдем период решетки:
d =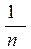 . (8)
. (8)
Подставляя (8) в формулу (7), получим:
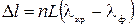 . (9)
. (9)
Произведем вычисления
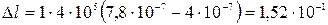 м = 15,2 см.
м = 15,2 см.
Для определений числа спектральных линий красного цвета найдем максимальное значение кmах, исходя из того, что максимальный угол отклонения лучей не может превышать 90° (sin 90° = 1). Из формулы (1) напишем:
к =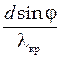 ,
,
следовательно, кmax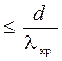 . С учетом (8) получим:
. С учетом (8) получим:
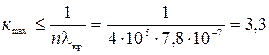 .
.
Так как число кmах должно быть обязательно целым, то кmах= 3. Влево и вправо от центра картины будет наблюдаться одинаковое число спектральных линий, равное 2кmах. Таким образом, общее число спектральных линий равно 2кmах = 6.
Так как разрешающая способность дифракционной решетки
R=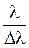 =кN,(10)
=кN,(10)
то минимальная разница длин волн двух спектральных линий, разрешаемых решеткой,
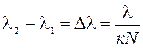 . (11)
. (11)
Две спектральные линии разрешены, если
 . (12)
. (12)
Полагая l = l1, получаем
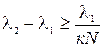 . (13)
. (13)
Из выражения (13) следует, что спектральные линии разрешены в спектрах с порядком
 . (14)
. (14)
Число щелей решетки определяется выражением 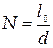 , или с учетом формулы (8)
, или с учетом формулы (8)
N = 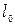 n. (15)
n. (15)
Подставляя (15) в (14), получим:
 . (16)
. (16)
Произведем вычисления
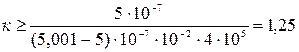 .
.
Так как к – целое число, то к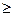 2.
2.
5.2.8. Поляризация света
1) Закон Брюстера
tg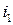 = n21,
= n21,
где i1– угол падения, при котором отразившийся от диэлектрика луч полностью поляризован; n21 = n2/n1 – относительный показатель преломления второй среды относительно первой.
2) Закон Малюса
I = Incos 2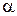 ,
,
где In – интенсивность плоскополяризованного света, падающего на анализатор; I – интенсивность этого света после анализатора; a – угол между направлением колебаний светового вектора волны, падающей на анализатор и плоскостью пропускания анализатора (плоскостью поляризации).
3) Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество:
— в твердых телах
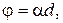
где a – постоянная вращения; d – длина пути, пройденного светом в оптически активном веществе;
— в растворах
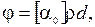
где a0 – удельное вращение; 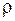 – массовая концентрация оптически активного вещества в растворе.
– массовая концентрация оптически активного вещества в растворе.
Примеры решения задач
Задача 1
Во сколько раз уменьшится интенсивность естественного света при прохождении через две призмы Николя, угол между плоскостями поляризации которых равен 60o. Потери света в каждой призме составляют 10 % (рис. 5).
 A I1
A I1
I0 I2
N1 N2
Рис. 5
Обыкновенный луч, подчиняясь закону преломления, преломляется и, подойдя к слою канадского бальзама в призме (граница АВ), испытывает полное отражение и поглощается зачерненной боковой гранью призмы. Необыкновенный луч проходит через призму. Таким образом, на выходе поляризатора получается плоскополяризованный свет, интенсивность которого с учетом потерь на отражение и поглощение света поляризатором равна
 ,(1)
,(1)
где I0 – интенсивность естественного света, падающего на поляризатор; к – коэффициент, учитывающий потери на отражение и поглощение.
Плоскополяризованный луч света, падая на вторую призму Николя (анализатор), также расщепляется на обыкновенный и необыкновенный лучи. Обыкновенный луч полностью поглощается призмой. Необыкновенный луч проходит через призму. После прохождения анализатора интенсивность света уменьшается как за счет отражения и поглощения света анализатором, так и из-за несовпадения плоскости поляризации света с плоскостью пропускания анализатора. В соответствии с законом Малюса и с учетом потерь на отражение и преломление света интенсивность равна
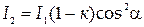 , (2)
, (2)
где a – угол между плоскостями поляризации поляризатора и анализатора. Подставляя выражение (1) в (2), имеем
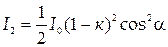 . (3)
. (3)
Относительное уменьшение интенсивности света при прохождении света через 2 призмы Николя равно
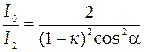 . (4)
. (4)
Подставив в расчетную формулу (4) значение к = 0,1; α = 60о, получим : 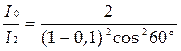 = 9,88.
= 9,88.
Задание на контрольную работу № 4
401. Точка совершает гармонические колебания с периодом 2 с. Амплитуда колебаний 10 см. Найти смещение, скорость и ускорение точки спустя 0,2 с после ее прохождения через положение равновесия. Начало колебаний связано с положением равновесия.
402. Чему равно отношение кинетической энергии точки, совершающей гармонические колебания, к ее потенциальной энергии для момента времени t = T/12, где Т – период колебаний?
403. Пружинный маятник совершает гармонические колебания с амплитудой смещения 0,04 м. При смещении 0,03 м сила упругости равна 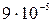 Н. Определить потенциальную и кинетическую энергии, соответствующие данному смещению, и полную энергию маятника.
Н. Определить потенциальную и кинетическую энергии, соответствующие данному смещению, и полную энергию маятника.
404. Определить максимальное ускорение материальной точки, совершающей гармонические колебания с амплитудой 15 см, если её наибольшая скорость равна 30 см/с. Написать уравнение колебаний, если начальная фаза равна 60о.
405. Максимальная скорость точки, совершающей гармонические колебания равна 10 см/с, максимальное ускорение 100 см/с2. Найти период и амплитуду колебаний.
406.Материальная точка массой 0,1 г совершает гармонические колебания с амплитудой 2 см и периодом 2 с. Начальная фаза колебаний равна нулю. Написать уравнение этих колебаний и определить максимальное значение скорости, а также максимальную силу, действующую на точку.
407. Материальная точка массой 20 г совершает колебания, уравнение которых имеет вид x = 0,3cos( 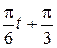 ), где смещение х – в метрах. Определить максимальные значения скорости и ускорения точки, полную механическую энергию точки и силу, действующую на точку в момент времени 2 с.
), где смещение х – в метрах. Определить максимальные значения скорости и ускорения точки, полную механическую энергию точки и силу, действующую на точку в момент времени 2 с.
408. Материальная точка массой 0,01 кг совершает гармонические колебания, уравнение которых имеет вид х=0,05sin6πt (смещение в сантиметрах, время в секундах). Найти возвращающую силу в момент времени t = 5 с, а также максимальную кинетическую энергию точки.
409. Найти максимальную кинетическую энергию материальной точки массой 2 г, совершающей гармонические колебания с амплитудой 4 см и частотой 5 Гц. Написать уравнение колебаний, если начальная фаза 30о.
410. Полная энергия тела, совершающего гармонические колебания, равна 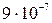 Дж. Амплитуда колебаний
Дж. Амплитуда колебаний 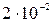 м. Определить смещение, при котором на тело действует сила
м. Определить смещение, при котором на тело действует сила 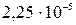 Н, и максимальную силу.
Н, и максимальную силу.
411. Период затухающих колебаний 4 с, логарифмический декремент затухания 1,6, начальная фаза равна нулю. Смещение точки при 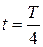 равно 4,5 см. Написать уравнение колебаний точки и построить его график в пределах двух периодов.
равно 4,5 см. Написать уравнение колебаний точки и построить его график в пределах двух периодов.
412. Уравнение колебаний тела имеет вид 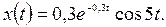 Определить моменты времени, в которые смещение максимально; вычислить добротность колебательной системы.
Определить моменты времени, в которые смещение максимально; вычислить добротность колебательной системы.
413. К вертикальной спиральной пружине подвешен стальной шарик радиусом 2 см. Циклическая частота его колебаний в воздухе 5 с-1, а в некоторой жидкости – 4,06 с-1. Начальное смещение 5 см. Определить коэффициент вязкости жидкости, записать уравнение колебаний шарика.
414. Гиря массой 0,5 кг подвешена к спиральной пружине жёсткостью 20 Н/м. и совершает колебания в некоторой среде. Логарифмический декремент затухания равен 0,004. Определить число полных колебаний, через которое амплитуда колебаний уменьшится в 2 раза. Через какое время это произойдёт?
415. Чему равен логарифмический декремент затухания математического маятника, если за 1 минуту амплитуда колебаний уменьшилась в 2 раза? Длина маятника 1 м.
416. Коэффициент затухания успокоителя колебаний стрелки измерительного прибора равен 2с-1. Через один период амплитуда колебаний уменьшилась в два раза. Через сколько колебаний амплитуда составит 1 % от первоначальной?
417. Тело массой 1г совершает затухающие колебания с частотой 3,14 с-1. В течение 50 с тело потеряло 80 % своей механической энергии. Определить коэффициент затухания, коэффициент сопротивления среды и добротность системы.
418. Определить период затухающих колебаний, если период собственных колебаний системы равен 1с и логарифмический декремент затухания равен 0,628.
419. Логарифмический декремент затухания маятника равен 0,003. Определить число колебаний, которое должен сделать маятник, чтобы амплитуда уменьшилась в два раза.
420. За один период колебаний система теряет 97 % энергии. Во сколько раз изменится амплитуда колебаний за это время? За какое время амплитуда уменьшится в 10 раз, если частота колебаний равна 14 с-1?
421. Катушка с индуктивностью 30 мГн и резистор включены последовательно в цепь переменного тока с действующим значением напряжения 220 В и частотой 50 Гц. Найти сопротивление резистора и действующее значение напряжения на нем, если сдвиг фаз между колебаниями силы тока и напряжения 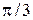 .
.
422. В цепь переменного тока с действующим значением напряжения 220 В и частотой 50 Гц включены последовательно конденсатор электроемкостью 1 мкФ и реостат с активным сопротивлением 300 Ом. Найти полное сопротивление цепи и действующее значение силы тока.
423. В цепь переменного тока с действующим значением напряжения 220 В и частотой 50 Гц включены последовательно резистор сопротивлением 100 Ом, конденсатор электроемкостью 32 мкФ и катушка индуктивностью 640 мГн. Найти действующее значение силы тока, сдвиг фаз между силой тока и напряжением и потребляемую мощность.
424. Катушка длиной 50 см и площадью поперечного сечения 10 см2 включена в цепь переменного тока с частотой 50 Гц. Число витков катушки 3000. Найти активное сопротивление катушки, если сдвиг фаз между силой тока и напряжением 60°.
425. Переменное напряжение, действующее значение которого 220 В, а частота 50 Гц, подано на катушку без сердечника индуктивностью 31,8 мГн и активным сопротивлением 10 Ом. Найти количество теплоты, выделяющейся в катушке за одну секунду.
426. К зажимам генератора присоединен конденсатор электроемкостью 0,15 мкФ. Определить амплитудное значение напряжения на зажимах, если амплитудное значение силы тока 3,3 А, а частота тока составляет 5 кГц.
427. В катушке с активным сопротивлением 10 Ом при частоте переменного тока 50 Гц сдвиг фаз между колебаниями напряжения и силы тока равен 60о. Определить индуктивность катушки.
428. Электропечь, сопротивление которой 22 Ом, питается от генератора переменного тока. Определить количество теплоты, выделяемое печью за 1 час, если амплитуда силы тока 10 А.
429. Сила тока в колебательном контуре изменяется со временем по закону I = 0,02sin400  t (A). Индуктивность контура 0,5 Гн. Найти период собственных колебаний в контуре, электроемкость контура, максимальную энергию электрического и магнитного полей.
t (A). Индуктивность контура 0,5 Гн. Найти период собственных колебаний в контуре, электроемкость контура, максимальную энергию электрического и магнитного полей.
430. Колебательный контур состоит из конденсатора и катушки индуктивности. Определить частоту колебаний, возникающих в контуре, если максимальная сила тока в катушке индуктивности 1,2 А, максимальная разность потенциалов на обкладках конденсатора 1200 В, полная энергия контура 1,1 мДж.
431.Два одинаково направленных гармонических колебания с одинаковой частотой и амплитудами 3 см и 5 см складываются в одно колебание с амплитудой 7 см. Найти разность фаз складываемых колебаний.
432. Точка участвует в двух колебаниях одинакового периода с одинаковыми начальными фазами. Амплитуды колебаний 3 см и 4 см. Найти амплитуду результирующего колебания, если: 1) колебания совершаются в одном направлении; 2) колебания взаимно перпендикулярны.
433. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых имеют вид х = sin(t/2), y = соst. Найти уравнение траектории точки. Построить траекторию с соблюдением масштаба и указать направление движения точки.
434. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях х = sinπt, y = 4sin(πt π). Найти траекторию движения точки, построить ее с соблюдением масштаба.
435. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых x = 3cost, y = 2sint. Найти траекторию точки, построить ее и указать направление движения точки.
436. Складываются два колебания одного направления с одинаковыми периодами, равными 1,5 с, и амплитудами, равными 2 см. Начальная фаза первого колебания равна  , второго
, второго 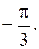 Определить амплитуду и начальную фазу результирующего колебания. Записать его уравнение и построить векторную диаграмму.
Определить амплитуду и начальную фазу результирующего колебания. Записать его уравнение и построить векторную диаграмму.
437. Движение точки задано уравнениями 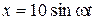 и
и 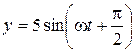 .
. 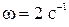 . Найти уравнение траектории. Вычислить скорость точки в момент времени 0,5 с.
. Найти уравнение траектории. Вычислить скорость точки в момент времени 0,5 с.
438. Материальная точка участвует в двух колебаниях 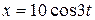 и
и 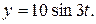 Записать уравнение траектории, выражения для скорости и ускорения точки.
Записать уравнение траектории, выражения для скорости и ускорения точки.
439. Смещение материальной точки по двум взаимно перпендикулярным направлениям описывается уравнениями 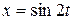 и
и  Записать уравнение траектории; найти зависимость линейной скорости от времени; вычислить максимальную скорость.
Записать уравнение траектории; найти зависимость линейной скорости от времени; вычислить максимальную скорость.
440. Складываются три колебания одного направления с одинаковыми периодами, равными 1,5 с; амплитудами, равными 3 см; фазами 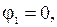
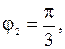
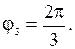 Построить векторную диаграмму положения амплитуд. Определить из чертежа амплитуду и начальную фазу результирующего колебания, записать его уравнение.
Построить векторную диаграмму положения амплитуд. Определить из чертежа амплитуду и начальную фазу результирующего колебания, записать его уравнение.
441. Уравнение плоской звуковой волны, распространяющейся вдоль оси х, имеет вид у = 60cos(1800t – 5,3x), где смещение у – в микрометрах. Определить длину волны, скорость распространения волны и максимальную скорость колебаний частиц среды.
442. Звуковые колебания, имеющие частоту 500 Гц и амплитуду 0,25 мм, распространяются в воздухе. Длина волны 70 см. Найти скорость распространения волны и максимальную скорость колебаний частиц воздуха.
443. Найти смещение от положения равновесия и скорость точки, отстоящей от источника колебаний на расстоянии l/12, для момента времени Т/6. Амплитуда колебания 0,05 м.
444. Плоская звуковая волна возбуждается источником колебаний частотой 200 Гц. Амплитуда колебаний источника равна 4 мм. Написать уравнение волны, если в начальный момент смещение точек максимально. Найти смещение точек среды на расстоянии 1 м от источника в момент времени 0,1 с. Скорость звуковой волны 300 м/с. Затуханием пренебречь.
445. В воздухе распространяется плоская акустическая волна со скоростью 340 м/с. Смещение точек волны описывается уравнением 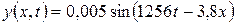 см. Определить длину волны, амплитуду колебаний, скорость колебаний молекул воздуха, интенсивность волны.
см. Определить длину волны, амплитуду колебаний, скорость колебаний молекул воздуха, интенсивность волны.
446. Плоская звуковая волна имеет период 3 мс, амплитуду 0,2 мм и длину волны 1,2 м. Для точек среды, находящихся от источника колебаний на расстоянии 2 м, найти: смещение, скорость, ускорение точек в момент 7 мс.
447. Входной контур радиоприемника состоит из катушки индуктивностью 2 мГн и плоского конденсатора с площадью пластин 10 см2 и расстоянием между ними 2 мм. Пространство между пластинами заполнено слюдой с диэлектрической проницаемостью 7. На какую длину волны настроен радиоприемник?
448. Резонанс в колебательном контуре с конденсатором электроемкостью 1 мкФ наступает при частоте 4000 Гц. Если параллельно первому конденсатору подключить второй конденсатор, то резонансная частота становится равной 2000 Гц. Определить электроемкость второго конденсатора.
449. В однородной изотропной немагнитной среде с диэлектрической проницаемостью равной 3 распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны 10 В/м. Найти амплитуду напряженности магнитного поля и фазовую скорость волны.
450. Плоская электромагнитная волна распространяется в вакууме. Амплитуда напряженности электрического поля волны 50 мВ/м. Найти амплитуду напряженности магнитного поля и среднее за период колебаний значение плотности потока энергии.
451. Расстояние от щелей до экрана в опыте Юнга равно 1 м. Определить расстояние между щелями, если на отрезке длиной 1 см укладывается 10 темных интерференционных полос. Длина волны монохроматического света равна 0,7 мкм.
452. Установка для наблюдения колец Ньютона освещается монохроматическим светом с длиной волны 590 нм. Свет падает по нормали к поверхности пластины. Между линзой и пластинкой находится жидкость с показателем преломления 1,33. Определить толщину зазора в том месте, где в отраженном свете наблюдается третье светлое кольцо.
453. В опыте Юнга расстояние между щелями равно 0,8 мм, длина волны света 0,7 мкм. На каком расстоянии от щелей следует расположить экран, чтобы ширина интерференционной полосы оказалась равной 2 мм?
454. Радиус второго темного кольца Ньютона в отраженном свете равен 0,4 мм. Определить радиус кривизны плосковыпуклой линзы, взятой для опыта, если она освещается монохроматическим светом с длиной волны 0,5 мкм.
455. Расстояние между двумя когерентными источниками света равно 0,2 мм. Они удалены от экрана на расстояние 2 м. Найти длину волны, излучаемую когерентными источниками, если расстояние на экране между третьим и пятым минимумами интерференционной картины равно 1,2 см.
456. Между стеклянной пластиной и лежащей на ней плосковыпуклой линзой находится жидкость. Найти показатель преломления жидкости, если радиус третьего темного кольца Ньютона при наблюдении в отраженном свете с длиной волны 0,5 мкм равен 0,85 мм. Радиус кривизны линзы равен 0,64 м.
457. В опыте Юнга на пути одного из лучей помещена тонкая стеклянная пластинка, вследствие чего центральная полоса сместилась в положение занятое 5-й светлой полосой (не считая центральной). Луч падает на пластинку перпендикулярно. Показатель преломления пластинки 1,5. Длина волны  м. Какова толщина пластинки?
м. Какова толщина пластинки?
458. На стеклянную пластинку нанесен слой прозрачного вещества с показателем преломления 1,3. На пластинку падает нормально параллельный пучок монохроматического света с длиной волны 640 нм. Какую минимальную толщину должен иметь слой, чтобы отраженные лучи были максимально ослаблены в результате интерференции?
459. Входное окно фотоприемника покрыто тонкой пленкой, материал которой имеет показатель преломления 1,25. Толщина пленки равна 0,20 мкм. На какой наибольшей длине волны достигается максимальное просветление входного окна фотоприемника?
460. На пути одного из лучей в опыте Юнга поставлена трубка длиной 2 м с плоскопараллельными основаниями. При заполнении трубки хлором вся интерференционная картина на экране сместилась на 20 полос. Вычислить показатель преломления хлора, считая, что показатель преломления воздуха 1,000276. Длина волны 589 нм.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
В контрольную работу № 5 включены задачи на следующие темы: тепловое излучение; фотоэффект; строение атома; спектры атомов; элементы квантовой механики; физика твердого тела; физика атомного ядра; радиоактивность.
Для решенния задач 501…510 по теме “Тепловое излучение” необходимо изучить его основные характеристики: энергетическая светимость, спектральная поглощательная и излучательная способность тел. Особенно важно усвоить законы излучения абсолютно черного тела как оптимального излучателя для тепловых источников.
Приступая к решению задач 501…510 проработайте соответствующий материал по учебному пособию [1], с. 367…373.
Исследованию квантовой природы внешнего фотоэффекта и его закономерностей посвящено решение задач 511…520. Предварительно необходимо ознакомиться с данным явлением, рассмотреть вольт-амперную и световую характеристики, изучить этот материал по пособию [1], с. 376…381.
Решение задач 521…530 требует понимания квантовой природы спектров излучения атомов, на примере атома водорода. Следует уяснить, что излучение атомом света происходит при переходе электрона с высшего энергетического уровня на низкий. При этом излучается один квант (фотон), частота которого определяется разностью энергий соответствующих уровней. Если в задаче не указаны номера каких-либо энергетических уровней, то их можно определить по принадлежности излучения к той или иной части спектра. Проработайте этот материал по учебному пособию [1], с. 387…389, 412…426.
Задачи 531…550 на тему “Элементы квантовой механики” требуют понимания корпускулярно-волнового дуализма микрочастиц (знание волн де Бройля и их свойств), а также знание соотношения неопределенностей как границы применимости классических представлений к микрочастицам квантовой природы.
Приступая к решению этих задач проработайте материал данной темы по пособию [1], с. 393…398.
Задачи 551…560 относятся к теме “Физика твёрдого тела”. Здесь нужно обратить внимание на зонную структуру энергетических зон твердых тел, изучить зависимость проводимости полупроводников от температуры, ознакомиться с эффектом Холла по учебному пособию [1], с. 442…450.
Исследованию элементов физики атомного ядра посвящено решение задач 561…580.
Задачи 561…570 посвящены радиоактивному излучению и закону радиоактивного распада. Проработайте этот материал по учебному пособию [1], с. 471…474.
Решение задач 571…580 требует знания состава ядра, понятий дефекта массы и энергии связи ядра, характеристик ядерных сил.
Решение задач 571…580 требует понимания закономерностей ядерных реакций, в частности законов сохранения. Обратить внимание на способ определения энергии реакции деления ядер.
Приступая к решению этих задач ознакомьтесь с этим материалом по учебному пособию [1], ч. 484…493.
Табл. 5
6.2.Основные законы и формулы. Примеры решения задач
Тепловое излучение
1. Энергетическая светимость тела Re – это энергия, излучаемая единицей поверхности тела за единицу времени в диапазоне длин волн от 0 до 
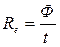 .
.
2. Поток Ф, излучаемый(поглощаемый) телом, равен
 ,
,
где W – энергия, излучаемая (поглощаемая) телом; t – время.
3. Закон Стефана-Больцмана
Re = sT4,
где Re – энергетическая светимость (излучательность) абсолютно черного тела; s = 5,67 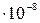 Вт/(
Вт/( 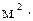 К4) – постоянная Стефана-Больцмана; Т – термодинамическая температура.
К4) – постоянная Стефана-Больцмана; Т – термодинамическая температура.
4. Первый закон Вина (закон смещения Вина)
lm = b/T,
где lm – длина волны, на которую приходится максимум излучения абсолютно черного тела; b = 2,90 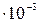
 К – постоянная первого закона Вина.
К – постоянная первого закона Вина.
5. Второй закон Вина
(rl,T)max = 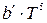 ,
,
где (rl,T)max – максимальная спектральная плотность энергетической светимости абсолютно черного тела; b’ = 1,3 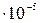 Вт / (К5
Вт / (К5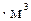 )– постоянная второго закона Вина.
)– постоянная второго закона Вина.
Примеры решения задач
Задача 1
Длина волны, на которую приходится максимум энергии в спектре излучения черного тела, 0,58 мкм. Определить энергетическую светимость поверхности тела.
Re = sT4, (1)
где s – постоянная Стефана-Больцмана; Т – термодинамическая температура.
Температуру Т можно вычислить с помощью закона Вина:
lm = b / T, (2)
где b – постоянная закона смещения Вина.
Используя формулы (2) и (1), получаем
Re = s(b/lm)4.
Произведем вычисления
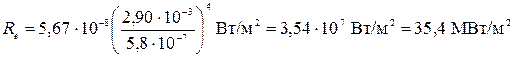 .
.
Фотоэффект
Энергия фотона
e = hnилиe = ħ 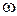 ,
,
где h – постоянная Планка; ħ = h/2p – приведенная постоянная Планка; 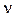 – частота фотона;
– частота фотона; 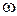 = 2
= 2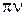 – циклическая частота.
– циклическая частота.
Импульс фотона
p = h/l.
Формула Эйнштейна для фотоэффекта
hn = A 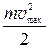 ,
,
где hn — энергия фотона, падающего на поверхность металла; А – работа выхода электрона; 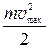 – максимальная кинетическая энергия фотоэлектронов.
– максимальная кинетическая энергия фотоэлектронов.
Красная граница фотоэффекта
no= A/h или lo= hc/A,
где no и lo – минимальная частота света и соответствующая длина волны, при которых еще возможен фотоэффект.
Примеры решения задач
Задача 1
Работа выхода материала фотокатода равна 3,4 эВ. Какова должна быть максимальная длина волны излучения, падающего на фотокатод, если фототок прекращается при разности потенциалов 1,2 В?
Авых – работа выхода электрона; 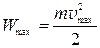 – максимальная кинетическая энергия фотоэлектронов.
– максимальная кинетическая энергия фотоэлектронов.
Максимальная кинетическая энергия фотонов равна работе сил задерживающего электрического поля, т.е.
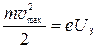 ,
,
где е – заряд электрона; 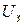 – задерживающая разность потенциалов. Минимальная энергия фотонов, при которой возможен фотоэффект, равна
– задерживающая разность потенциалов. Минимальная энергия фотонов, при которой возможен фотоэффект, равна  , где lmax – максимальная длина волны фотонов.
, где lmax – максимальная длина волны фотонов.
Подставим полученные соотношения в уравнение Эйнштейна, получим:
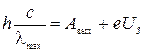 , откуда находим lmax:
, откуда находим lmax:
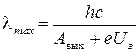 .
.
Подставим числовые значения
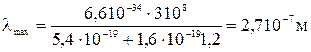
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
1. Полная энергия электрона в состоянии, характеризуемом главным квантовым числом n
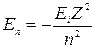 , (3)
, (3)
где Ei = Rhc – энергия ионизации атома водорода; Z – порядковый номер элемента в таблице Менделеева; Еi= 13,5 эВ.
2. Энергия, излучаемая или поглощаемая атомом водорода или водородоподобным ионом
E = h 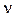
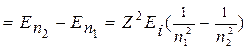 ,
,
где n1 и n2 – главные квантовые числа, соответствующие энергетическим состояниям, между которыми совершается переход электрона.
3. Сериальная формула для определения длины волны спектра излучения атома водорода (или водородоподобного иона)
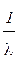 = RZ2
= RZ2  ,
,
где l – длина волны фотона; R – постоянная Ридберга.
Примеры решения задач
Задача 1
Атом водорода перешел из возбужденного состояния, характеризуемого главным квантовым числом, равным трем, в основное. Определить возможные спектральные линии в спектре излучения водорода. Найти максимально возможную энергию фотона.
Из рисунка видно, что при переходе атома из состояния, характеризуемого главным квантовым числом n = 3, в основное (n = 1), возможно излучение трех спектральных линий.
Для определения длины волны воспользуемся сериальной формулой для водородоподобных ионов
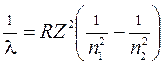 ,
,
где l – длина волны фотона; R – постоянная Ридберга; Z – заряд ядра в относительных единицах (при Z = 1 формула переходит в сериальную формулу для водорода); n1 – главное квантовое число состояния, в которое перешел атом; n2 – главное квантовое число исходного состояния.
Найдем длину волны линии, излученной при переходе атома из состояния n2 = 3 в состояние n1 = 2, приняв постоянную Ридберга 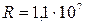 м-1:
м-1:
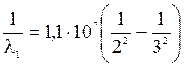 ,
, 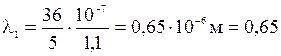 мкм.
мкм.
Аналогично находим длину волны спектральной линии, излученной атомом при переходе из состояния n2 = 2 в состояние n1 = 1.
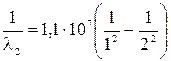 ,
,  мкм.
мкм.
При переходе из состояния n2 = 3 в состояние n1 = 1 длина волны линии равна
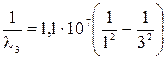 ,
, 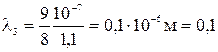 мкм.
мкм.
Энергия фотона определяется из выражения
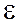 ф = hc/
ф = hc/  ,
,
где h – постоянная Планка, h =  10-34 Дж
10-34 Дж 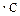 , с – скорость света в вакууме, с =
, с – скорость света в вакууме, с = 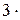 108м/с.
108м/с.
Максимальная энергия фотона соответствует минимальной длине волны, следовательно
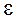 ф = hc/
ф = hc/ 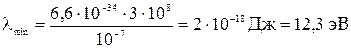 .
.
Элементы квантовой механики
1. Длина волны де Бройля
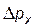 ,
,
где p – импульс частицы.
2. Если кинетическая энергия частицы много меньше энергии покоя (Еk << E0), то для определения импульса частиц можно пользоваться классическим выражением, т.е.
p = mv = 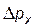 ,
,
где кинетическая энергия частицы 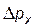 .
.
3. Если кинетическая энергия частицы Ek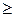 E0, то импульс частицы следует вычислять по формуле релятивистской механики, т.е.
E0, то импульс частицы следует вычислять по формуле релятивистской механики, т.е.
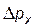 ,
,
где Ео – энергия покоя частицы; Ек – кинетическая энергия частицы, равная
Ек = m0c2  ,
,
где m0 – масса покоя частицы; v – скорость частицы.
4. Соотношения неопределенностей:
а) для координаты и импульса ∆px∆x≥ћ/2,
где 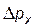 – неопределенность проекции импульса на ось x;
– неопределенность проекции импульса на ось x;
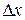 – неопределенность координаты x;
– неопределенность координаты x;
б) для энергии и времени ∆E∆t≥ћ/2,
где 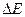 – неопределенность энергии;
– неопределенность энергии; 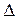 t – время жизни квантовой системы в данном энергетическом состоянии.
t – время жизни квантовой системы в данном энергетическом состоянии.
Примеры решения задач
Задача 1
Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля для двух случаев: 1) U1 = 51 B; 2) U2 = 510 кВ.
Импульс частицы можно определить, если известна ее кинетическая энергия Ек. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше энергии ее покоя) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы):
— в нерелятивистском случае
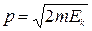 , (2)
, (2)
— в релятивистском случае
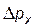 , (3)
, (3)
где 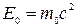 – энергия покоя частицы.
– энергия покоя частицы.
Формула (1) с учетом соотношений (2) и (3) запишется:
— в нерелятивистском случае
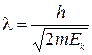 , (4)
, (4)
— в релятивистском случае
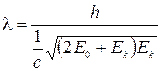 . (5)
. (5)
Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U1 = 51 В и U2 = 510 кВ, с энергией покоя электрона и, в зависимости от этого, решим, которую из формул – (4) или – (5) следует применить для вычисления длины волны де Бройля.
Как известно, кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, равна
Eк = eU.
В первом случае
Ек = eU1 = 51 эВ = 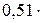 10-4 МэВ, что много меньше энергии покоя электрона, равной
10-4 МэВ, что много меньше энергии покоя электрона, равной 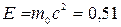 МэВ.
МэВ.
Следовательно, в этом случае можно применить формулу (4). Для упрощения расчетов заметим, что Ек = 10-4m0c2. Подставив это выражение в формулу (4), перепишем ее в виде
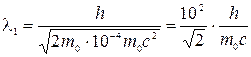 .
.
Учитывая, что h/moc есть комптоновская длина волны 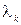 , получим:
, получим:
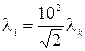 .
.
Так как 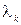 = 2,43 пм, то
= 2,43 пм, то
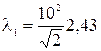 пм = 171 пм.
пм = 171 пм.
Во втором случае кинетическая энергия
Eк = eU2 = 510 кэВ = 0,51 МэВ,
т.е. равна энергии покоя электрона. В этом случае необходимо применить релятивистскую формулу (5). Учитывая, что Ек = 0,51 МэВ = moc2, по формуле (5) найдем
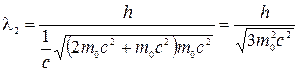 ,
,
или 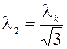 .
.
Подставив значение 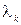 и произведя вычисления, получим:
и произведя вычисления, получим:
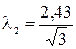 пм = 1,40 пм.
пм = 1,40 пм.
Задача 2
Кинетическая энергия электрона в атоме водорода составляет величину порядка 10 эВ. Используя соотношение неопределенностей, оценить минимальные размеры атома.
координаты частицы (в данном случае электрона); ħ = h/2p – приведенная постоянная Планка h.
Из соотношения неопределенностей следует, что чем точнее определяется положение частицы в пространстве, тем более неопределенным становится импульс, а следовательно, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где-то в пределах области с неопределенностью
Δx = l / 2.
Cоотношение неопределенностей можно записать в этом случае в виде
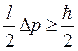 ,
,
откуда
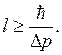
Физически разумная неопределенность импульса Δp, во всяком случае, не должна превышать значение самого импульса p, т. е. Δp ≤ p.
Импульс р связан с кинетической энергией Ек соотношением
р = 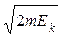 .
.
Заменим 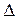 р значением
р значением 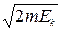 (такая замена не увеличит l). Перейдем к равенству
(такая замена не увеличит l). Перейдем к равенству
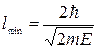 .
.
Подставив числовые значения и произведя вычисления, получим:
lmin = 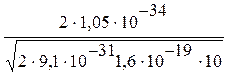 м =
м = 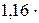 10-10 м = 116 пм.
10-10 м = 116 пм.
Задача 3. Оценить относительную ширину испускаемой спектральной линии, длина волны которой составляет 0,6 мкм, при переходе атома из возбужденного в основное состояние. Время жизни атома в возбужденном состоянии оставляет приблизительно  .
.
Частота испускаемого фотона связана с длиной волны соотношением
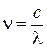 ,
,
где с – скорость света в вакууме.
Искомая величина 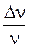 равна
равна 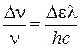 .
.
Для нахождения Δε воспользуемся соотношением неопределенностей для энергии и времени ∆ε∆t ≥ ћ/2,
где 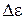 – неопределенность энергии;
– неопределенность энергии; 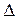 t – время жизни атома в возбужденном энергетическом состоянии.
t – время жизни атома в возбужденном энергетическом состоянии.
∆ε = ћ/2∆t.
Подставим ∆ε в искомую величину, получим:
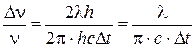 .
.
Подставим числовые значения и находим
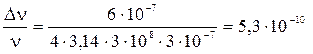 .
.
Физика твердого тела
1. Удельная электропроводность полупроводника
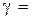 e(nun pup),
e(nun pup),
где е – заряд электрона; n и p – концентрация носителей заряда (подвижных электронов и дырок); un и up – подвижности электронов и дырок.
В случае проводимости одного типа одним из слагаемых в выражении (1) можно пренебречь. Для чистого, беспримесного полупроводника проводимость называется собственной и в формуле для 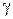 следует положить n = p.
следует положить n = p.
2. Зависимость собственной удельной электропроводности полупроводника от температуры
 ,
,
где 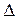 Е – ширина запрещенной зоны полупроводника;
Е – ширина запрещенной зоны полупроводника; 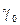 – константа, почти не зависящая от температуры; k – постоянная Больцмана.
– константа, почти не зависящая от температуры; k – постоянная Больцмана.
3. Холловская разность потенциалов равна
Uн = Rн  I,
I,
где В – индукция магнитного поля; а – толщина образца; I – сила тока в образце; 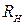 – постоянная Холла.
– постоянная Холла.
4. Для полупроводника с кристаллической решеткой типа алмаза (Ge, Si) с примесной проводимостью одного типа постоянная Холла равна
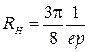 .
.
Примеры решения задач
Задача 1
До какой температуры нужно нагреть образец из арсенида галлия, находящегося при температуре 0  , чтобы его проводимость возросла в 4 раза?
, чтобы его проводимость возросла в 4 раза?
где 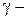 постоянная;
постоянная; 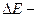 ширина запрещенной зоны; k – постоянная Больцмана.
ширина запрещенной зоны; k – постоянная Больцмана.
Таким образом, 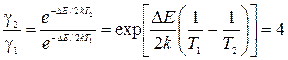 .
.
Прологарифмируем выражение и получим:
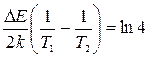 ,
,
откуда
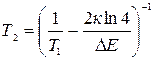 .
.
Полагая для арсенида галлия DЕ = 1,43 эВ, произведем вычисления
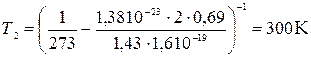 .
.
Задача 2
Некоторый примесный полупроводник имеет решетку типа алмаза и обладает только дырочной проводимостью. Определить концентрацию носителей и их подвижность, если постоянная Холла равна 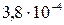 м3/Кл. Удельная проводимость полупроводника 110
м3/Кл. Удельная проводимость полупроводника 110  .
.
Rн = 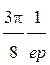 ,
,
где е – элементарный заряд.
Отсюда
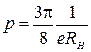 . (1)
. (1)
Запишем все величины в единицах СИ: е =  10-19 Кл;
10-19 Кл; 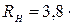 10-4 м3/Кл.
10-4 м3/Кл.
Подставим числовые значения величин в формулу (1) и произведем вычисления
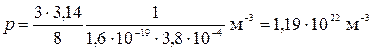 .
.
Удельная проводимость  полупроводников выражается формулой
полупроводников выражается формулой
 = e(nun pup), (2)
= e(nun pup), (2)
где n и p – концентрации электронов и дырок; un и up – их подвижности.
При отсутствии электронной проводимости первое слагаемое в скобках равно нулю и формула (2) примет вид
 = epup.
= epup.
Отсюда искомая подвижность
up = 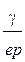 . (3)
. (3)
Подставим в (3) выражение р по формуле (1)
up = 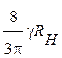 . (4)
. (4)
Подставив в (4) значения 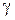 и
и 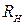 и произведя вычисления, получим:
и произведя вычисления, получим:
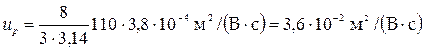 .
.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
1. Обозначение ядра химического элемента:
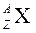 ,
,
где Х – химический символ элемента; А – массовое число (число нуклонов в ядре)
А =(Z N);
Z – зарядовое число (число протонов); N – число нейтронов.
2. Закон радиоактивного распада
N = Noexp(– 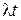 ),
),
где N – число ядер, нераспавшихся к моменту времени t; No– число ядер в начальный момент времени (t = 0); 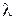 – постоянная распада.
– постоянная распада.
3. Связь периода полураспада с постоянной распада
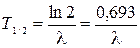 .
.
Число ядер, распавшихся за время t ,
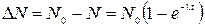 .
.
4. В случае если интервал времени 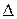 t, за который определяется число распавшихся ядер, много меньше периода полураспада
t, за который определяется число распавшихся ядер, много меньше периода полураспада 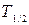 , то
, то
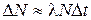 .
.
5. Среднее время жизни 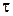 радиоактивного ядра, т.е. интервал времени, за который число нераспавшихся ядер уменьшается в е раз,
радиоактивного ядра, т.е. интервал времени, за который число нераспавшихся ядер уменьшается в е раз,
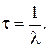
6. Число атомов N, содержащихся в радиоактивном изотопе,
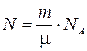 ,
,
где m – масса изотопа; 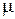 – молярная масса; NA – постоянная Авогадро.
– молярная масса; NA – постоянная Авогадро.
7. Активность А радиоактивного изотопа
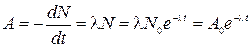 ,
,
где dN – число ядер, распавшихся за интервал времени dt; Ао – активность изотопа в начальный момент времени.
В системе СИ единица активности препарата – беккерель (Бк)
1 Бк = 1 распад/с.
Внесистемная единица активности – кюри (Ки)
1 Ки =  1010 Бк.
1010 Бк.
1 Кюри – это активность препарата изотопа радия-226 массой 1 г.
8. Дефект массы ядра
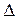 m = Zmp Nmn — mя,
m = Zmp Nmn — mя,
где mp – масса протона; mn – масса нейтрона; mя– масса ядра.
9. Энергия связи ядра
Есв= 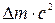 ,
,
где Dm – дефект массы ядра; с – скорость света в вакууме.
Есв = 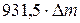 МэВ,
МэВ,
где дефект массы  выражен в атомных единицах массы (а.е.м.), 931,5 – энергетический эквивалент 1 а.е.м.
выражен в атомных единицах массы (а.е.м.), 931,5 – энергетический эквивалент 1 а.е.м.
10. Удельная энергия связи равна Есв/ А [МэВ/нуклон].
Примеры решения задач
Задача 1
Вычислить дефект массы, энергию связи и удельную энергию связи ядра 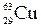 .
.
Решение:
Дефект массы
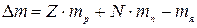 , где
, где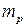 – масса протона;
– масса протона; 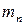 – масса нейтрона; Z – количество протонов; N – количество нейтронов в ядре; mя – масса ядра атома.
– масса нейтрона; Z – количество протонов; N – количество нейтронов в ядре; mя – масса ядра атома.
Так как в справочной литературе всегда приводятся массы нейтральных атомов m, но не ядер, формулу для дефекта массы целесообразно преобразовать.
Масса нейтрального атома 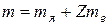 , где
, где 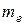 – масса электрона.
– масса электрона.
Откуда 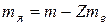 . Следовательно, дефект массы будет равен
. Следовательно, дефект массы будет равен
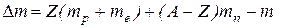 .
.
Учитывая, что 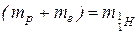 , где
, где 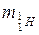 – масса атома водорода, для дефекта массы окончательно получим выражение:
– масса атома водорода, для дефекта массы окончательно получим выражение:
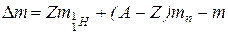 .
.
В данной задаче для меди Z = 29, N = A – Z = 63 – 29 = 34
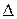 m = (29×1,00783 34×1,00867 – 62,92960) а.е.м. = 0,59191 а.е.м.
m = (29×1,00783 34×1,00867 – 62,92960) а.е.м. = 0,59191 а.е.м.
1 а.е.м. = 1,6605655 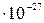 кг = 1,66×10–27 кг
кг = 1,66×10–27 кг
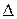 m = 0,59191а.е.м.
m = 0,59191а.е.м. 
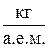 = 0,98257
= 0,98257 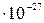 кг
кг
Есвязи = 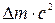 = 0,98257
= 0,98257 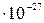 кг
кг 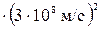 = 8,84314
= 8,84314 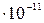 Дж,
Дж,
т.к. 1 эВ = 1,6 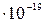 Дж
Дж
Есв.= 5,527 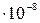 эВ=552 МэВ.
эВ=552 МэВ.
Энергия связи, приходящаяся на 1 нуклон (удельная энергия связи),
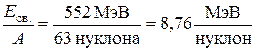 .
.
Примечание
Ответ 552 МэВ можно было получить короче, если учесть, что энергетический эквивалент 1 а.е.м. равен 931,5 МэВ, тогда
Есв.= 0,59191а.е.м. 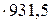 МэВ = 552 МэВ.
МэВ = 552 МэВ.
1а.е.м. = 1,66 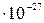 кг.
кг.
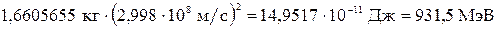 .
.
Задача 2
Определить начальную активность радиоактивного препарата магния-27 массой 0,2 мкг, а также его активность через 6 часов.
А = 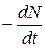 , (1)
, (1)
знак «–» показывает, что число N радиоактивных ядер с течением времени убывает.
Чтобы найти dN/dt, воспользуемся законом радиоактивного распада
 , (2)
, (2)
где N – число радиоактивных ядер, содержащихся в изотопе в момент времени t; No – число радиоактивных ядер в момент времени, принятый за начальный (t = 0); 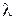 – постоянная распада.
– постоянная распада.
Продифференцируем выражение (2) по времени
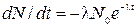 . (3)
. (3)
Исключив из формул (1) и (3) dN/dt, находим активность препарата в момент времени t
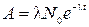 . (4)
. (4)
Начальную активность Ао препарата получим при t = 0
Ао = 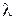 No . (5)
No . (5)
Постоянная радиоактивного распада 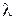 связана с периодом полураспада Т1/2 соотношением
связана с периодом полураспада Т1/2 соотношением
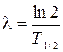 . (6)
. (6)
Число No радиоактивных ядер, содержащихся в изотопе, равно произведению постоянной Авогадро NA на количество вещества 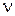 данного изотопа
данного изотопа
No = 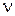 NA =
NA = 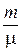 NA, (7)
NA, (7)
где m – масса изотопа; m – молярная масса.
С учетом вырaжений (6) и (7) формулы (5) и (4) принимают вид:
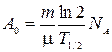 , (8)
, (8)
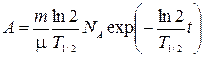 . (9)
. (9)
Произведя вычисления и учитывая, что Т1/2 = 600 с; ln2 = 0,693; t = 6 ч = 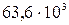 с =
с = 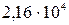 с, получим:
с, получим:
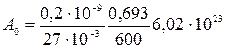 Бк =
Бк = 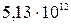 Бк =
Бк =  Кu,
Кu,
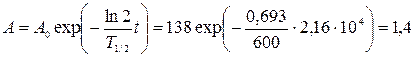 Кu.
Кu.
Задача 3
Определить расход урана-235 в ядерном реакторе атомной электростанции за 1 сутки. Электрическая мощность электростанции равна 15 МВт, КПД электростанции составляет 20 %. Считать, что при каждом акте деления ядра урана-235 выделяется энергия 200 МэВ.
Выразим тепловую энергию электростанции, вырабатываемую за время t:
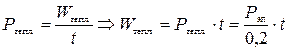 .
.
Исходя из этих данных, найдем число распавшихся атомов N за сутки:
N = 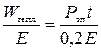 .
.
Выразим массу урана, распавшегося за сутки
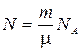 ,
,
где N – количество атомов, распавшихся за сутки; m – молярная масса урана ( 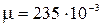 кг/моль); NA – число Авогадро (
кг/моль); NA – число Авогадро ( 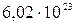 моль-1).
моль-1).
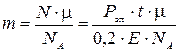 .
.
Подставим числовые значения
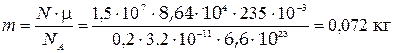 .
.
Задание на контрольную работу № 5
501. Абсолютно черное тело имеет температуру 500К. Какова будет температура тела, если в результате нагревания поток излучения увеличится в 5 раз? Исходя из формулы Планка, изобразить графически начальный и конечный спектры излучения.
502. Температура абсолютно черного тела равна 2000К. Определить длину волны, на которую приходится максимум спектра энергии излучения, и спектральную плотность энергетической светимости для этой длины волны.
503. Определить температуру и энергетическую светимость абсолютно черного тела, если максимум энергии спектра излучения приходится на длину волны 600 нм.
504. Из смотрового окошечка печи излучается поток 4 кДж/мин. Определить температуру печи, если площадь окошечка равна 8 см2.
505. Поток излучения абсолютно черного тела равен 10 кВт, а максимум спектра излучения приходится на длину волны 0,8 мкм. Определить площадь излучающей поверхности.
506. Как и во сколько раз изменится поток излучения абсолютно черного тела, если максимум видимого спектра излучения переместится с красной границы спектра 780 нм на фиолетовую 390 нм?
507. Вычислить энергию (в кВт 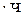 ), излучаемую за сутки с площади 0,5 м2 нагревателя, температура которого 70 оС. Считать, что нагреватель излучает как серое тело с коэффициентом поглощения 0,3.
), излучаемую за сутки с площади 0,5 м2 нагревателя, температура которого 70 оС. Считать, что нагреватель излучает как серое тело с коэффициентом поглощения 0,3.
508. Печь, потребляющая мощность 1 кВт, имеет отверстие площадью 100 см2. Определить долю мощности, рассеиваемую стенками печи, если температура ее внутренней поверхности равна 1000К.
509. При остывании абсолютно черного тела максимум его спектра излучения сместился на 500 нм. На сколько градусов остыло тело? Начальная температура тела 2000К.
510. Определить мощность, необходимую для накаливания вольфрамовой нити электролампы длиной 10 см и диаметром нити 1 мм до температуры 3000К. Коэффициент поглощения нити 0,34.
511. Красная граница фотоэффекта для цинка составляет 310 нм. Определить максимальную кинетическую энергию (в электрон-вольтах) фотоэлектронов и задерживающую разность потенциалов, если на цинк падает ультрафиолетовое излучение с длиной волны 200 нм.
512. Фотоэлектроны, вылетающие с поверхности серебряной пластины, полностью задерживаются при приложении задерживающей разности потенциалов, равной 8 В. Найти длину волны излучения, падающего на фотокатод.
513. Фотон с энергией 10 эВ выбивает электроны из серебряной пластины. Определить импульс, полученный пластиной, если принять, что направления импульсов фотона и фотоэлектрона перпендикулярны поверхности пластины.
514. На поверхность фотокатода падает ультрафиолетовое излучение с длиной волны 0,3 мкм. Задерживающая разность потенциалов, при которой фототок прекращается, равна 1,6 В. Определить красную границу фотоэффекта.
515. Какова должна быть длина волны излучения, падающего на платиновую пластину, если максимальная скорость фотоэлектронов равна 3 Мм/с?
516. Ультрафиолетовое излучение с длиной волны 0,25 мкм, направленное на металлическую пластину, вызывает фототок, который прекращается при минимальной задерживающей разности потенциалов 0,96 В. Определить работу выхода электрона из металла.
517. На поверхность металла падает ультрафиолетовое излучение с длиной волны 0,1 мкм. Красная граница фотоэффекта равна 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?
518. На поверхность лития падает рентгеновское излучение с длиной волны 1 нм. Определить максимальную скорость фотоэлектронов. Можно ли пренебречь работой выхода электрона?
519. Две пластины, одна из которых медная, а другая из неизвестного материала, освещаются ультрафиолетовым излучением из одного и того же источника. Для фотоэлектронов из медной пластины задерживающая разность потенциалов равна 2,4 В, а для неизвестной пластины она равна 4,2 В. Найти работу выхода электронов из неизвестного материала.
520. Красная граница фотоэффекта для вольфрама равна 275 нм. Определить задерживающую разность потенциалов для электронов, вырываемых из вольфрама светом с длиной волны 180 нм.
521. Фотон, соответствующий длине волны 0,020 мкм, выбил электрон из невозбужденного атома водорода. Вычислить скорость электрона за пределами атома.
522. Найти наибольшую и наименьшую длины волн в видимой области спектра излучения атома водорода.
523. Определить все возможные спектральные линии , возникающие при переходе атома водорода из возбужденного состояния с главным квантовым числом, равным 3, в основное.
524. Атом водорода в основном состоянии поглотил фотон с длиной волны 0,1215 мкм. Определить главное квантовое число возбужденного состояния атома водорода.
525. В водородоподобном ионе лития электрон перешел из состояния с главным квантовым числом, равным четырем, в состояние, характеризуемое главным квантовым числом, равным двум. Определить энергию кванта и длину волны излучения, испущенного ионом.
526. Какую наименьшую энергию должны иметь электроны, чтобы возбужденный этими электронами спектр водорода имел три спектральные линии?
527. Определить энергию фотона, испускаемого при переходе электрона в атоме водорода из возбужденного состояния с главным квантовым числом, равным трём, в основное состояние.
528. Определить диапазон длин волн монохроматического излучения, чтобы при возбуждении атома водорода этим излучением наблюдались три спектральные линии?
529. Как изменилась энергия электрона в атоме водорода при испускании атомом фотона с частотой 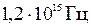 ?
?
530. Какой диапазон длин волн должно иметь монохроматическое излучение, чтобы при возбуждении атомов водорода этим излучением главное квантовое число возросло в 3 раза?
531. Определить неопределенность координаты электрона, движущегося в атоме водорода со скоростью 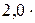 106 м/сек, если относительная неопределенность скорости равна 0,1. Сравнить полученную неопределенность с диаметром атома водорода, вычисленным по теории Бора для основного состояния, и указать, применимо ли понятие траектории в данном случае.
106 м/сек, если относительная неопределенность скорости равна 0,1. Сравнить полученную неопределенность с диаметром атома водорода, вычисленным по теории Бора для основного состояния, и указать, применимо ли понятие траектории в данном случае.
532. Электрон с кинетической энергией 10 эВ находится в металлической пылинке диаметром 1 мкм. Оценить (в процентах) относительную неопределенность скорости электрона.
533. Если допустить, что неопределенность координаты движущейся частицы равна дебройлевской длине волны, то какова будет относительная неопределенность импульса этой частицы?
534. Диаметр пузырька в жидководородной пузырьковой камере составляет величину порядка 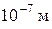 . Рассчитать неопределенность в измерении скоростей электрона и
. Рассчитать неопределенность в измерении скоростей электрона и 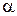 -частицы в такой камере, если неопределенность координаты принять равной диаметру пузырька.
-частицы в такой камере, если неопределенность координаты принять равной диаметру пузырька.
535. Используя соотношение неопределенностей, оценить наименьшую ошибку в определении импульса электрона и протона, если координаты этих частиц определяются с точностью 50 мкм.
536. Среднее время жизни атома в возбужденном состоянии составляет 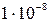 с. При переходе в основное состояние атом испустил фотон с длиной волны
с. При переходе в основное состояние атом испустил фотон с длиной волны 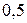 мкм. Оценить энергию фотона и неопределенность его длины волны.
мкм. Оценить энергию фотона и неопределенность его длины волны.
537. Атом испустил фотон с длиной волны 700 нм. Найти наибольшую точность, с которой может быть измерена длина волны излучения, если продолжительность излучения равна 40 нс.
538. Оценить относительное уширение спектральной линии 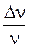 , если известны время жизни атома в возбужденном состоянии (~
, если известны время жизни атома в возбужденном состоянии (~ 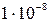 с) и длина волны излучаемого фотона, равная
с) и длина волны излучаемого фотона, равная  м.
м.
539. Время жизни возбужденного ядра составляет величину порядка 0,5 нс, длина волны излучения равна 0,2 нм. С какой наибольшей точностью может быть определена энергия излучения?
540. Среднее время жизни атома в возбужденном состоянии составляет примерно 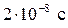 . При переходе атома в основное состояние испускается фотон, длина волны которого составляет 0,5 мкм. Оценить относительную ширину
. При переходе атома в основное состояние испускается фотон, длина волны которого составляет 0,5 мкм. Оценить относительную ширину 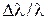 испускаемой спектральной линии.
испускаемой спектральной линии.
541. Найти длину волны де Бройля для электрона, если его кинетическая энергия равна энергии покоя.
542. Определить длину волны де Бройля для протона, движущегося со средней квадратичной скоростью при Т = 300 К.
543. 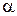 -частица движется в однородном магнитном поле с индукцией 5 мТл по окружности радиусом 0,8 м. Определить длину волны де Бройля
-частица движется в однородном магнитном поле с индукцией 5 мТл по окружности радиусом 0,8 м. Определить длину волны де Бройля 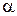 -частицы.
-частицы.
544. Длина волны де Бройля протона равна 2 нм. Какую ускоряющую разность потенциалов прошел протон?
545. Кинетическая энергия нейтрона равна 2 МэВ. Определить длину волны де Бройля нейтрона.
546. Кинетическая энергия протона равна его энергии покоя. Определить длину волны де Бройля для такого протона.
547. Какую ускоряющую разность потенциалов должен пройти электрон, чтобы длина волны де Бройля была равна 1,0 нм?
548. Найти длину волны де Бройля нейтрона, кинетическая энергия которого равна удвоенной энергии покоя.
549. Кинетическая энергия протона равна 1876 МэВ. Как и во сколько раз изменится длина волны де Бройля, если кинетическая энергия уменьшится в два раза?
550. Определить длину волны де Бройля протона, движущегося в магнитном поле с индукцией 1мТл по окружности радиусом 10 см.
551. Как изменится удельное сопротивление чистого арсенид-галлиевого образца при нагреве его от комнатной температуры до 400 К?
552. Определить ширину запрещенной зоны полупроводниковой пластины, если при нагревании от 0 до 10 градусов Цельсия её удельное сопротивление уменьшилось в 2,28 раз. Из какого материала изготовлена пластина?
553. Перпендикулярно однородному магнитному полю, индукция которого равна 0,1 Тл, помещена тонкая пластинка из примесного кремния. Толщина пластинки соответствует 400 мкм. Определить плотность тока, при которой холловская разность потенциалов достигнет значения 0,5 В. Постоянную Холла для кремния принять равной 0,3 м3/Кл.
554. Удельное сопротивление кремния р-типа равно 10–2 Ом 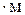 . Определить концентрацию дырок и их подвижность. Принять постоянную Холла равной
. Определить концентрацию дырок и их подвижность. Принять постоянную Холла равной 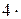 10–4 м3/Кл.
10–4 м3/Кл.
555. Тонкая пластинка из кремния р-типа толщиной 200 мкм расположена перпендикулярно силовым линиям однородного магнитного поля с индукцией 0,5 Тл. При плотности тока 2 мкА/мм2, направленного вдоль пластины, холловская разность потенциалов оказалась равной 2,8 В. Определить концентрацию носителей тока.
556. Концентрация носителей тока в чистом кремнии равна 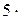 1010 см–3.Определить сопротивление кремниевого стержня длиной 2 см и сечением 1 мм2 при комнатной температуре.
1010 см–3.Определить сопротивление кремниевого стержня длиной 2 см и сечением 1 мм2 при комнатной температуре.
557. Вычислить постоянную Холла для кремния р-типа, если его удельное сопротивление равно 0,2 Ом 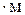 .
.
558. Кристалл из чистого германия, ширина запрещенной зоны которого равна 0,72 эВ, нагревают от температуры 0 оС до температуры 15 оС. Во сколько раз возрастает его удельная проводимость?
559. При нагревании кристалла из чистого кремния от температуры 0 оС до температуры 10 оС его удельная проводимость возрастает в 2,28 раза. По этим данным определить ширину запрещенной зоны кристалла кремния.
560. Найти удельное сопротивление чистого германиевого образца при температуре 100 оС, если при 20 оС оно составляет величину 0,5 Ом 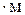 .
.
561. Определить, какая доля радиоактивного изотопа 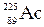 распадается в течение 6 суток.
распадается в течение 6 суток.
562. Активность некоторого изотопа за 10 суток уменьшилась на 20 %. Определить период полураспада этого изотопа.
563. Определить массу изотопа 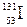 , имеющего активность, равную 37 ГБк.
, имеющего активность, равную 37 ГБк.
564. Найти среднюю продолжительность жизни атома радиоактивного изотопа кобальт 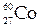 .
.
565. Счетчик a-частиц, установленный вблизи радиоактивного изотопа, при первом измерении регистрировал 1400 частиц в минуту, а через 4 часа только 400 частиц. Определить период полураспада изотопа.
566. Во сколько раз уменьшится активность изотопа 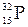 через 20 суток?
через 20 суток?
567. На сколько процентов уменьшится активность изотопа 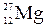 за 7 минут?
за 7 минут?
568. Определить число ядер, распадающихся в течение времени: 1) t1 = 1 мин; 2) t2 = 5 сут, – в радиоактивном изотопе фосфора 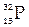 массой, равной 1 мг.
массой, равной 1 мг.
569. Из каждого миллиона атомов радиоактивного изотопа каждую секунду распадается 200 атомов. Определить период полураспада изотопа.
570. Найти период полураспада радиоактивного изотопа, если его активность за 10 суток уменьшилась на 24 % по сравнению с первоначальной.
571. Считая, что в одном акте деления ядра 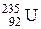 освобождается энергия 200 МэВ, определить энергию, выделяющуюся при делении одного килограмма изотопа
освобождается энергия 200 МэВ, определить энергию, выделяющуюся при делении одного килограмма изотопа 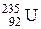 , и массу каменного угля с удельной теплотой сгорания 30 кДж/г, эквивалентную в тепловом отношении одному килограмму
, и массу каменного угля с удельной теплотой сгорания 30 кДж/г, эквивалентную в тепловом отношении одному килограмму 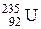 .
.
572. При бомбардировке изотопа 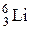 дейтронами образуются две
дейтронами образуются две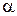 -частицы, при этом выделяется энергия 22,3 МэВ. Зная массы дейтрона и
-частицы, при этом выделяется энергия 22,3 МэВ. Зная массы дейтрона и 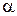 — частицы, найти массу изотопа
— частицы, найти массу изотопа 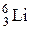 в атомных единицах массы.
в атомных единицах массы.
573. Найти дефект массы и энергию связи трития 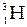 . Какой процент от энергии покоя ядра составляет его энергия связи?
. Какой процент от энергии покоя ядра составляет его энергия связи?
574. Найти удельную энергию связи 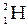 и
и 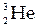 . Какое из этих ядер более устойчиво?
. Какое из этих ядер более устойчиво?
575. Найти минимальную энергию  — кванта, достаточную для осуществления реакции деления первоначально покоившегося дейтрона
— кванта, достаточную для осуществления реакции деления первоначально покоившегося дейтрона  — лучами:
— лучами: 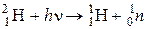 .
.
576. Найти электрическую мощность атомной электростанции, расходующей 0,1 кг урана-235 в сутки, если КПД станции равен 30 %. Считать энергию, выделяющуюся при одном акте деления ядра урана-235, равной 200 МэВ.
577. Найти тепловую мощность атомного реактора, расходующего 0,1 кг урана-235 в сутки. Считать энергию, выделяющуюся при одном акте деления ядра урана-235, равной 200 МэВ.
578. Найти электрическую мощность атомной электростанции при условии, что убыль массы ТВЭЛ-ов (стержней, содержащих ядерное горючее) составляет 100 г в сутки. КПД станции равен 31 %.
579. Найти электрическую мощность атомного реактора, расходующего 0,1 кг урана-235 в сутки. КПД реактора составляет 18%. Считать энергию, выделяющуюся при одном акте деления ядра урана-235, равной 200 МэВ.
580. Определить КПД атомной станции мощностью 20 МВт, если суточный расход ядерного горючего при работе станции составляет 75 г урана-235. Считать, что при каждом акте деления ядра урана-235 выделяется энергия 200 МэВ.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
Методические указания к выполнению контрольной работы № 6
Контрольная работа включает задания по следующим темам дисциплины “Физика твёрдого тела”: пространственная решетка кристалла; теплоемкость и теплопроводность кристаллов; электронный газ в металлах; собственные и примесные полупроводники, p-n-переход; диффузия носителей тока; эффект Холла.
Задачи с 1 по 13 относятся к теме “Пространственная решётка кристалла”. Приступая к решению этих задач проработайте материал пособия [3], c. 12…18. Выпишите и разберите такие определения как: узел решётки, атомная плоскость, элементарная ячейка, трансляции, типы решёток, координационное число, индексы Миллера.
Задачи с 14 по 27 относятся к теме “Теплоемкость и теплопроводность кристаллов”. Проработайте материал пособия [3], c. 44…61. Рассмотрите и усвойте понятия: нормальные колебания решётки, фононы, дебаевская частота и дебаевская температура, закон Дюлонга-Пти.
Задачи с 28 по 31 относятся к теме “Электронный газ в металлах”. Проработайте материал пособия [3], c. 32…42.
Задачи с 32 по 46 относятся к теме “Собственные и примесные полупроводники”. Проработайте материал пособия [3], c.86…106.
Задачи с 47 по 51 и с 57 по 61 относятся к теме “Диффузия носителей тока. р-n-переход”. Проработайте материал пособия [3], c. 106…109. и с. 113…117.
Задачи с 52 по 56 относятся к теме “Эффект Холла”. Проработайте материал пособия [3], c. 117…119.
Табл. 6
7.2. Основные законы и формулы. Примеры решения задач
Пространственная решетка кристалла
1. Координаты любого узла решетки записываются в виде
 ;
; 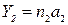 ;
; 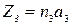 и обозначаются: [[n1n2n3]], где ai – основные периоды решетки; ni – целые числа, называемые индексами узла и обозначающие число периодов решетки, соответствующих данному узлу,
и обозначаются: [[n1n2n3]], где ai – основные периоды решетки; ni – целые числа, называемые индексами узла и обозначающие число периодов решетки, соответствующих данному узлу, 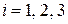 .
.
Для описания направления в кристалле выбирают прямую, проходящую через начало координат. Ее направление однозначно определяется индексаминаправления [n1n2n3], где ni – индексы ближайшего к началу координат узла решетки.
2. Период идентичности вдоль прямой, заданной индексами [n1n2n3], в кубической решетке выражается соотношением
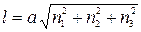 ,
,
где а – параметр решетки.
3. Кристаллографическиеплоскости определяются тремя взаимно простыми целыми числами (hkl), называемыми индексамиМиллера. Они определяют систему бесконечного числа параллельных между собой плоскостей, каждая из которых характеризуется определенным значением числа
q = 0, 1, 2, …
Таким образом, кристаллографическая плоскость однозначно задается совокупностью чисел {(hkl), q}. Для отрицательных индексов над (или под) буквой ставится знак минус, например h. Индексы [[n1n2n3]] любого узла, лежащего в данной плоскости, удовлетворяют соотношению:
n1h n2k n3l = q.
При q = 0 плоскость проходит через начало координат.
Если плоскость параллельна какой-либо оси координат, то соответствую-щий индекс Миллера равен нулю. Так, плоскость (110) параллельна оси z, а плоскость (100) параллельна плоскости (yz).
4. Расстояние D плоскости от начала координат определяется числом q
D = q/b0,
где
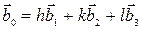 ,
,
где 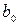 – вектор обратной решетки;
– вектор обратной решетки; 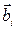 (i = 1,2,3) – базисные векторы обратной решетки
(i = 1,2,3) – базисные векторы обратной решетки
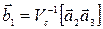 ,
, 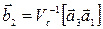 ,
, 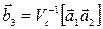 ;
;
Vc– объем элементарной ячейки кристалла.
Из выражения 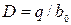 следует, что расстояние d между соседними плоскостями (Dq = 1) с индексами (hkl) равно:
следует, что расстояние d между соседними плоскостями (Dq = 1) с индексами (hkl) равно:
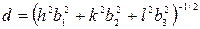 .
.
5. Кристаллические плоскости отсекают на осях координат отрезки, равные
xq = а1q/h, yq = a2q/k, zq = a3q/l
Очевидно, что если q/h, q/k и q/l – целые числа, то плоскость пересекает соответствующую координатную ось в узловой точке.
6. Молярный объем кристалла
Vm = m/r,
где m – молярная масса; r – плотность кристалла.
7. Объем элементарной ячейки в случае кубической сингонии
Vэл = а3,
где а – параметр решетки.
8. Число элементарных ячеек в одном моле кристалла
Zm = Vm/Vэл
Если кристалл состоит из одинаковых атомов, то
Zm = NA/n,
где NA – число Авогадро; n – число одинаковых атомов, приходящихся на элементарную ячейку.
9. Число элементарных ячеек в единице объема кристалла
Z=Zm/Vm.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
Z = rNA/(nm)
10. Параметр решетки, состоящей из одинаковых атомов
a = (nm/rNA )1/3
Расстояние между соседними атомами в кубической решетке:
а) в простой d = a;
б) в гранецентрированной 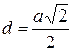 ;
;
в) в объемноцентрированной 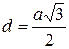 .
.
11. Число одинаковых атомов, приходящихся на элементарную ячейку:
а) простая кубическая решетка n = 1;
б) гранецентрированная кубическая решетка n = 4;
в) объемноцентрированная кубическая решетка n = 2.
Примеры решения задач
Задача 1
Определить параметр решетки и плотность кристалла кальция, если расстояние между ближайшими соседними атомами равно 0,393 нм. Решетка кубическая, гранецентрированная.
Подставляя в это выражение числовые значения, получим:
а = 5,56 10-10 м.
Плотность кристалла
r = mn/(NAa3) = 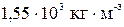 .
.
Задача 2
Вычислить период идентичности l вдоль прямой [2 3 1] в решётке NaCl, если плотность кристалла равна 2,17 г/см3. Решётка гранецентрированная кубическая.
Для гранецентрированной решетки число узлов в элементарной ячейке 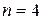 . Пользуясь таблицей Менделеева, находим: A(Na) = 23, A(Cl) = 35. Следовательно, M(NaCl) = 58, откуда молярная масса NACl:
. Пользуясь таблицей Менделеева, находим: A(Na) = 23, A(Cl) = 35. Следовательно, M(NaCl) = 58, откуда молярная масса NACl:
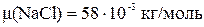 .
.
Подставляя числа в формулу (1), получаем
а = 5,62 10-10 м.
Период идентичности кристалла вдоль прямой [231]
l = a(n12 n22 n32)1/2 = 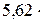 10-10 (4 9 1)1/2 = 13,3 10-10 м
10-10 (4 9 1)1/2 = 13,3 10-10 м
Задача 3
Написать индексы Миллера для плоскости, проходящей через узлы с индексами: [[010]], [[122]], [[132]]. Найти отрезки, отсекаемые этими плоскостями на осях координат.
| Дано: Индексы узлов: [[010]], [[122]], [[132]]. | Решение: Для любого узла с индексами [[n1n2n3]], лежащего в данной плоскости, индексы Миллера (hkl) удовлетворяют соотношению: n1h n2k n3l = q, (1) |
| (hkl) =?, xq=?, yq=?, zq=? |
где h, k, l, q – целые числа. Подставляя в уравнение (1) последовательно индексы всех трех узлов, получаем систему уравнений:
k = q
h k – 2l = q
h 3k 2l =q
Решая эту систему в целых числах, получаем: h = -6, k = 4, l = -1; q = 4, т.е. данная плоскость задается индексами: {(641);4}. Она отсекает на осях координат отрезки, равные
x0 = a1q/h = -2/3 a1; y0 = a2q/k = a2; z0 = -4a3,
где аi(i = 1,2,3) – основные периоды решетки. Плоскость пересекает оси у и z в узловых точках.
Теплоемкость и теплопроводность кристаллов
1. Согласно закону Дюлонга и Пти, молярная теплоемкость химически простых твердых тел при температурах, больших температуры Дебая QD:
Cm = 3R,
где R = 8,31 Дж/(моль 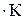 ) универсальная газовая постоянная.
) универсальная газовая постоянная.
Для химически сложных тел (состоящих их атомов различных химических элементов) – закон Неймана-Коппа:
Cm = 3nR,
где n – общее число частиц в химической формуле соединения.
2. Удельная теплоемкость:
— для химически простых
с = Cm/m;
— для химически сложных веществ
 .
.
3. Энергия фонона e связана с круговой частотой колебаний w соотно-шением
 ,
,
где 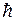 = h/(2p) =
= h/(2p) = 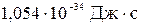 .
.
4. Квазиимпульс фонона
p = h /l,
где h = 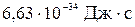
5. Скорость 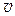 фонона (скорость звуковых волн в кристалле в пренебрежении дисперсией)
фонона (скорость звуковых волн в кристалле в пренебрежении дисперсией)
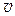 = wl/(2p).
= wl/(2p).
6. Частота Дебая (максимальная частота колебаний кристаллической решетки)
wD = 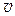 (6p2n)1/3 ,
(6p2n)1/3 ,
где n = N/V – концентрация атомов в кристалле,
n = NAr/m,
где r — плотность кристалла; m — молярная масса.
7. Температура Дебая:
 ,
,
где k – постоянная Больцмана, k = 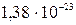 Дж/K.
Дж/K.
8. Поток тепловой энергии Q, проходящий через поперечное сечение S стержня в единицу времени
Q = -l(dT/dx)S,
где l — теплопроводность; dT/dx – градиент температуры.
l = 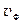 l
l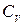 /3,
/3,
где 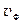 – групповая скорость фононов; l – средняя длина свободного пробега фононов между двумя последовательными столкновениями;
– групповая скорость фононов; l – средняя длина свободного пробега фононов между двумя последовательными столкновениями; 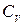 – теплоемкость единицы объема.
– теплоемкость единицы объема.
9. Молярная теплоемкость кристаллической решетки при температуре T<<  :
:
Cm = 12p4R (T/  )3/5 = 234R(T/
)3/5 = 234R(T/  )3.
)3.
Примеры решения задач
Задача 1
Вычислить по классической теории теплоемкость кристалла бромида алюминия (AlBr3) объемом 200 см3. Плотность кристалла бромида алюминия равна 3,01 г/см3. Условие T >  считать выполненным.
считать выполненным.
Сm = n 3R = 99,7 Дж/моль К.
Теплоемкость всего кристалла
C = Cmm/m = CmrV/m = 12RrV/m. (1)
По таблице Менделеева находим: A(Al) = 27, A(Br) = 80, следовательно M(AlBr3) = 267, а m = 0,267 кг/моль. Подставляя в формулу (1) числа, получаем
С = 225 Дж/K.
Задача 2
Вычислить длину волны фононов в свинце, соответствующую частоте w = 0,1wD, если плотность свинца 11,3 г/cм3, а молярная масса 207 г/моль.
где 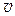 – средняя скорость распространения колебаний (скорость звука) в кристалле; n – концентрация атомов в кристалле,
– средняя скорость распространения колебаний (скорость звука) в кристалле; n – концентрация атомов в кристалле,
n = NAr/m . (2)
В пренебрежении дисперсией звука в кристалле:
lF = 2p 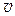 /w,
/w,
или, согласно условию задачи,
lF = 20p 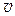 /wD .
/wD .
Окончательно, пользуясь формулами (1) и (2), получаем
lF = 20p(6p2NAr/m)-1/3 (3)
Подставляя в формулу (3) NA = 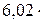 1023 и числовые данные из условия задачи, будем иметь: lF =
1023 и числовые данные из условия задачи, будем иметь: lF = 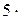 10-9 м.
10-9 м.
Задача 3
Определить температуру Дебая для серебра, если известно, что для нагревания серебра массой 15 г от температуры 5 К до температуры 10 К надо затратить количество тепла 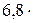 10-2 Дж. Условие T<<
10-2 Дж. Условие T<<  считать выполненным.
считать выполненным.
С = Cmm/m (2)
Подставляя (2) в (1) и интегрируя по температуре от Т1 до Т2, получаем
Q = (3p4mR/5m  3) [T24 – T14]. (3)
3) [T24 – T14]. (3)
Выразим из формулы (3) температуру Дебая:
 = ((3p4mR/5mQ)[T24 – T14])1/3. (4)
= ((3p4mR/5mQ)[T24 – T14])1/3. (4)
Произведем вычисления по формуле (4), учтя, что у серебра молярная масса равна m = 0,108 кг/моль:  = 210 K.
= 210 K.
Электронный газ в металлах
1. Концентрация электронов dn(e), энергия которых заключена в интервале значений от Е до Е dЕ:
dn(Е) = (2m*)3/2 (2p2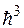 )-1Е1/2 (
)-1Е1/2 ( 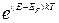 1) -1,
1) -1,
где m* и Е – эффективная масса и энергия электрона; m =EF – энергия Ферми.
2. При Т = 0
EF = ( 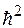 /2m*) (3p2n) 2/3.
/2m*) (3p2n) 2/3.
3. Средняя энергия электронов при Т = 0:
<E> = 3/5 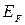
4. Температура Ферми
TF = 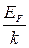 .
.
5. Температура вырождения
Тв = 4/(9p) 1/3TF = 1,313TF.
Примеры решения задач
Задача 1
Определить температуру вырождения для калия, если считать, что на каждый атом приходится по одному свободному электрону. Плотность калия r = 860 кг/м3.
| Дано: r(K) = 860 кг/м3 | Решение: Температура вырождения ТB согласно квантовой теории электронов в металле определяется выражением: ТB = h2n2/3/(2pkm), (1) |
| ТB = ? |
где h = 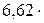 10-34 Дж·с – постоянная Планка; k = 1,38 10-23 Дж/К – постоянная Больцмана; m =
10-34 Дж·с – постоянная Планка; k = 1,38 10-23 Дж/К – постоянная Больцмана; m = 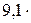 10-31кг – масса электрона; n – концентрация квазисвободных электронов в металле. Согласно условию, n равно концентрации N атомов, которая определяется выражением:
10-31кг – масса электрона; n – концентрация квазисвободных электронов в металле. Согласно условию, n равно концентрации N атомов, которая определяется выражением:
N = NAr/m, (2)
где NA – число Авогадро; r — плотность кристалла; m — молярная масса калия. По таблице Менделеева: m =  10-3 кг/моль.
10-3 кг/моль.
Полагая n = N и подставляя выражение (2) в формулу (1) с учетом приведенных выше числовых данных окончательно получаем
ТВ = 3,12 104 К.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
1. Сила прямого тока в p–n-переходе:
J = Js[exp(eU/kT) – 1],
где U – внешнее напряжение, приложенное к p–n-переходу в прямом направлении (( ) к р-области, (–) к n-области); Js – предельное значение обратного тока (ток насыщения). Сила обратного тока: 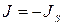 ,
, 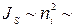 [–Eg/(kT)].
[–Eg/(kT)].
2. Коэффициенты диффузии электронов Dnи дырок Dp
Dn = kTun/e; Dp = kTup/e,
где е =  10-19 Кл – заряд электрона; un и up – подвижности электронов и дырок соответственно.
10-19 Кл – заряд электрона; un и up – подвижности электронов и дырок соответственно.
3. Коэффициент амбиполярной диффузии
Dэфф = (n p)/(n/Dp p/Dn),
где n и р – концентрация электронов и дырок соответственно.
Для собственного полупроводника (n = p):
Dэфф = 2DnDp/(Dn Dp).
4. Диффузионная длина L:
L = (Dэффt)1/2,
где t – время жизни неравновесных носителей тока.
5. Концентрация неравновесных носителей тока:
Dn(x) = Dn(0) e—x/L,
где Dn(0) – концентрация неравновесных носителей тока в месте их образования, например, на поверхности освещенного полупроводника; х – координата (расстояние от освещенной поверхности полупроводника); L – диффузионная длина.
Примеры решения задач
Задача 1
На расстоянии 0,48 мм от освещенной поверхности собственного кремния концентрация неравновесных носителей тока спадает в 3 раза. Определить время жизни неравновесных носителей тока, если температура кремния 300 К, а подвижность электронов и дырок при этой температуре соответственно 1500 cм2/(В  ) и 500 cм2/(В
) и 500 cм2/(В 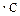 ). Собственная концентрация в Si при данной температуре 1010 см-3.
). Собственная концентрация в Si при данной температуре 1010 см-3.
Dn(x) = n(o)e—x/L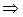 Dn(x)/Dn(0) = e—x/L
Dn(x)/Dn(0) = e—x/L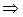 ln(Dn(x)/Dn(0)) = –x/L.
ln(Dn(x)/Dn(0)) = –x/L.
Следовательно,
L = x(ln(Dn(0)/Dn(x))) = 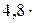 10-4/ln3 =
10-4/ln3 = 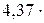 10-4 м.
10-4 м.
Чтобы найти коэффициент амбиполярной диффузии, надо сначала найти коэффициенты диффузии электронов и дырок:
Dn = kTun/e; Dp = kT up/e.
Подставляя числа, получаем:
Dn = 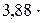 10-3 м2/с; Dp =
10-3 м2/с; Dp = 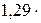 10-3 м2/c.
10-3 м2/c.
Для собственного полупроводника (n=p=ni) коэффициент амбиполярной диффузии равен:
Dэфф = 2DnDp/(Dn Dp) = 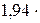 10-3 м2/c.
10-3 м2/c.
И, наконец, вычисляем время жизни неравновесных носителей тока:
t = L2/Dэфф = 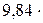 10-3 с.
10-3 с.
Эффект Холла
1. При не слишком сильных магнитных полях холловская разность потенциалов UH пропорциональна магнитной индукции поля В, силе тока I и обратно пропорциональна толщине пластины b:
UH = RH BI/b = RH Bja, (1)
где j – плотность тока в образце; а – ширина образца; RH – постоянная Холла, зависящая от материала образца.
2. Для полупроводников со смешанной проводимостью, у которых концентрации электронов и дырок сравнимы друг с другом, постоянная Холла вычисляется из следующего соотношения:
RH = 3p(pup2 – nun2)/[8e(pup nun)2], (2)
где n и р – концентрации электронов и дырок, соответственно; un и up – подвижности электронов и дырок соответственно.
а) Для полупроводников р-типа выражение для RH примет вид
RH = 3p/(8ep);
б) Для полупроводников n – типа (при n>>p):
RH= 3p/(8en);
в) Для собственных полупроводников, в которых 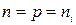 , выражение (2) принимает вид
, выражение (2) принимает вид
RH= 3p(up – un)/[8eni(up un)].
Примеры решения задач
Задача 1
Тонкая пластина из кремния n-типа шириной 2 см помещена перпендикулярно линиям индукции однородного магнитного полявеличиной 0,5 Тл. При плотности тока, направленной вдоль пластины, равной 2мкА/мм2, холловская разность потенциалов оказалась равной 2,8 В. Определить концентрацию основных носителей тока.
| Дано: а = 0,02 м В = 0,5 Тл j = 2 А/м2UH = 2,8 B | Решение: В данной задаче рассматривается полупроводник n-типа, для которого постоянная Холла определяется из соотношения: RH = 3p/(8en). (1) |
| n = ? |
Чтобы определить концентрацию n носителей, нужно знать постоянную Холла RH, которую можно выразить из формулы для холловской разности потенциалов:
UH= RH Bja.
Отсюда
RH= UH/(Bja). (2)
Приравняем правые части выражений (1) и (2):
3p/(8en) = UH/(Bja).
Отсюда получим концентрацию основных носителей тока
n = 3pBja/(8eUH). (3)
Подставляя в формулу (3) числовые значения, получим:
n = 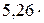 1016 м-3.
1016 м-3.
Задания на контрольную работу № 6
601. Вычислить период идентичности вдоль направления [021] в решетке AgBr, если плотность кристалла равна 3,87 г/см3. Решетка гранецентрированная кубическая.
602. Кристаллическая плоскость проходит через узлы [[110]], [[201]], [[321]] решетки. Написать индексы Миллера для этой плоскости.
603. Система плоскостей в примитивной кубической решетке задается индексами Миллера (312). Найти наименьшие отрезки, отсекаемые плоскостью на осях координат.
604. Написать индексы Миллера для двух плоскостей, содержащих узлы с индексами: а) [[113]], [[112]], [[101]] и б) [[211]], [[010]], [[111]]. Найти отрезки, отсекаемые этими плоскостями на осях координат.
605. Система плоскостей примитивной кубической решетки задана индексами (142). Определить расстояние между соседними плоскостями, если параметр решетки равен 0,3 нм.
606. Определить параметр примитивной кубической решетки, если межплоскостное расстояние для системы плоскостей, заданныx индексами Миллера (323), при рентгеноструктурном анализе оказалось равным 0,17 нм.
607. Три системы плоскостей в примитивной кубической решетке заданы индексами Миллера: а) (111); б) (011); в) (010). Определить отношения межплоскостных расстояний: d111 : d011 : d010.
608. Барий имеет объемноцентрированную кубическую решетку. Плотность кристалла бария равна 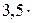 103
103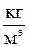 , а молярная масса
, а молярная масса  10–3
10–3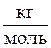 . Определить параметр решетки.
. Определить параметр решетки.
609. Золото имеет гранецентрированную кубическую решетку. Плотность золота принять равной  103 кг/м3, а молярную массу
103 кг/м3, а молярную массу 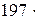 10-3
10-3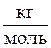 . Определить параметр решетки и расстояние между ближайшими соседними атомами.
. Определить параметр решетки и расстояние между ближайшими соседними атомами.
610. Определить число элементарных ячеек в единице объема кристалла меди. Решетка гранецентрированная кубическая. Плотность меди равна 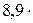 103
103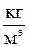 , а молярная масса
, а молярная масса 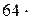 10 –3
10 –3 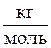 .
.
611. Молибден имеет объемноцентрированную кубическую решетку. Вычислить плотность молибдена и расстояние между ближайшими соседними атомами. Параметр решетки равен 0,315 нм, а молярная масса – 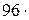 10–3
10–3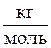 .
.
612. Найти плотность кристалла неона, если известно, что решетка гранецентрированная кубическая. Постоянная решетки равна 0,451 нм, а молярная масса 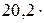 10-3
10-3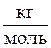 .
.
613. Определить молярную массу кристалла, если известно, что расстояние между ближайшими соседними атомами равно 0,304 нм. Решетка объемноцентрированная кубическая. Плотность кристалла 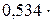 103
103 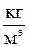 .
.
614. Пользуясь классической теорией, вычислить удельные теплоемкости кристаллов каменной соли и флюорита (KCl и CaF2). Относительные атомные массы: A (K) = 39; A(Cl) = 35; A(Ca) = 40; A(F) = 19.
615. Вычислить по классической теории теплоемкость кристалла NaCl объемом 100 см3. Плотность кристалла 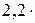 103
103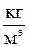 .
.
616.Определить изменение внутренней энергии кристалла корунда (Al2O3) при нагревании от 30 oC до 150 oC. Масса кристалла 30 г. Молярная масса Al:  10-3
10-3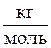 , кислорода:
, кислорода:  10-3
10-3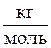 . Условие
. Условие 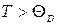 считать выполненным.
считать выполненным.
617. Вычислить частоту Дебая в кристалле золота. Для золота температура Дебая равна 180 К.
618. Медный образец массой 50 г находится при температуре 10 К. Определить количество теплоты, необходимое для его нагревания до температуры 15 К. Температуру Дебая для меди принять равной 300 К. Условие T<<QD считать выполненным. Молярная масса меди 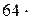 10 –3
10 –3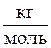 .
.
619. Вычислить по теории Дебая теплоемкость цинка массой 80г при температуре 12 К. Температура Дебая для цинка 308 К. Молярная масса цинка – 65·10-3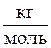 .
.
620. При нагревании серебра массой 10 г от температуры 10 К до температуры 20 К было затрачено количество теплоты 0,71 Дж. Определить температуру Дебая серебра. Условие T<<QD считать выполненным.
621. Используя теорию Дебая, вычислить удельную теплоемкость железа при температуре 15 К. Принять температуру Дебая для железа равной 467 К. Молярная масса железа 56 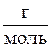 . Условие T<<QD считать выполненным.
. Условие T<<QD считать выполненным.
622. Вычислить частоту Дебая для серебра, если при температуре 20 К молярная теплоемкость равна 1,7 Дж/(моль 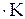 ).
).
623. Вода при температуре 0 oC покрыта слоем льда толщиной20 см. Температура воздуха равна –10 oC. Определить количество теплоты, переданной водой за время 1 час через поверхность льда площадью 10 см2. Теплопроводность льда 2,2 Вт/(м  ).
).
624. Вычислить длину волны фононов в вольфраме, соответствующую частоте w = 0,1wD, если для вольфрама плотность  103 кг/м3, молярная масса
103 кг/м3, молярная масса 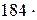 10 -3 кг/моль.
10 -3 кг/моль.
625. Вычислить среднюю длину свободного пробега фононов в кварце (SiO2), если теплопроводность кварца 13 Вт/(м  ), молярная теплоемкость 44 Дж/(моль
), молярная теплоемкость 44 Дж/(моль  ) и усредненная скорость звука 5 км/с. Плотность кварца
) и усредненная скорость звука 5 км/с. Плотность кварца  103 кг/м3.
103 кг/м3.
626. Температура Дебая для меди равна 309 К. Определить длину волны фононов, соответствующих частоте n = 0,1 nD и усредненную скорость звука в меди. Плотность меди 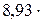 103
103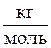 , молярная масса
, молярная масса 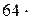 10 -3
10 -3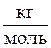 .
.
627. Длина волны фонона, соответствующего частоте w = 0,01 wD, равна 52 нм. Пренебрегая дисперсией звуковых волн, определить температуру Дебая QD, если усредненная скорость звука в кристалле равна 4,8 км/c.
628. Определить число свободных электронов, которое приходится на один атом Na при при температуре 0 К. Энергия Ферми равна 3,12 эВ, плотность кристалла 970 кг/м3.
629. Вычислить среднюю кинетическую энергию электронов в металле, если энергия Ферми равна 7 эВ.
630. Определить максимальную скорость электронов в металле при температуре 0 К, если энергия Ферми равна 5 эВ.
631. Определить среднюю дрейфовую скорость носителей тока в образце из натрия, если плотность тока, протекающего по образцу, равна 2 А/мм2, плотность кристалла натрия 970 кг/м3, а молярная масса 23 г/моль.
632. Собственный полупроводник при температуре 300 К имеет сопротивление 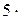 105 Ом. Если его нагреть до температуры 400 К, то его сопротивление уменьшится до
105 Ом. Если его нагреть до температуры 400 К, то его сопротивление уменьшится до 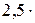 105 Ом. Найти ширину запрещенной зоны.
105 Ом. Найти ширину запрещенной зоны.
633. Кремниевый образец нагревают от температуры 0 оС до 10 оС. Во сколько раз возрастет его удельная проводимость? Ширину запрещенной зоны принять равной 1,12 эВ.
634. Образец собственного полупроводника германия при температуре 27 оС обладает удельным сопротивлением 0,47 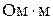 . Определить удельную проводимость германия при температуре 127 оС. Ширину запрещенной зоны принять равной 0,66 эВ.
. Определить удельную проводимость германия при температуре 127 оС. Ширину запрещенной зоны принять равной 0,66 эВ.
635. Во сколько раз изменится сопротивление германиевого образца, если его охладить от комнатной температуры 20 оС до температуры жидкого азота (77 К). Ширину запрещенной зоны считать равной 0,72 эВ.
636. Для приборов на основе германия предельная рабочая температура (температура, при которой собственная концентрация носителей тока становится сравнимой с примесной) равна 75 оС. Определить предельную рабочую температуру для приборов на основе кремния. Ширина запрещенной зоны германия равна 0,72 эВ, а кремния 1,1 эВ.
637. В чистом германии при температуре 300 К ширина запрещенной зоны равна 0,72 эВ. На сколько надо повысить температуру полупроводника, чтобы концентрация электронов в зоне проводимости увеличилась в два раза?
638. При температуре 300 К концентрация электронов в зоне проводимости равна 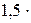 1016 м-3. Определить положение энергии Ферми относительно дна зоны проводимости и ширину запрещенной зоны при температуре 0 К. Плотность состояний в зоне проводимости принять равной
1016 м-3. Определить положение энергии Ферми относительно дна зоны проводимости и ширину запрещенной зоны при температуре 0 К. Плотность состояний в зоне проводимости принять равной 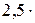 1025 м-3.
1025 м-3.
639. При температуре 300 К удельная электропроводность кремния равна 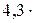 10-4
10-4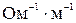 , подвижность электронов 0,135 м2/(В
, подвижность электронов 0,135 м2/(В 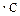 ), а подвижность дырок 0,048 м2/(В
), а подвижность дырок 0,048 м2/(В 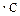 ). Определить концентрацию собственных носителей. Какая часть полного тока обусловлена электронами?
). Определить концентрацию собственных носителей. Какая часть полного тока обусловлена электронами?
640. Определить подвижность носителей тока в кремниевом образце толщиной 10 мкм, имеющем концентрацию электронов 1018 м-3, если при подаче на образец напряжения 5В через него протекает ток плотностью 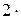 104 А/м2.
104 А/м2.
641. При температуре 300 К концентрация ионизированных примесей 1022 м-3. Найти положение уровня Ферми, приняв плотность состояний у дна зоны проводимости равной 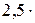 1025 м-3.
1025 м-3.
642. В образец кремния вводится примесь n-типа с концентрацией 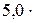 1023 м-3. После этого концентрация неосновных носителей в нем при температуре 300 К составляет
1023 м-3. После этого концентрация неосновных носителей в нем при температуре 300 К составляет 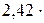 1010 м-3. Определить концентрацию собственных носителей ni в кремнии при температуре 300 К в предположении, что все примеси ионизированы.
1010 м-3. Определить концентрацию собственных носителей ni в кремнии при температуре 300 К в предположении, что все примеси ионизированы.
643. Считается, что полупроводниковый материал пригоден для использования в приборе, если при рабочих температурах концентрация собственных носителей  м-3. Определить максимальную рабочую температуруприборов на основе арсенида галлия (GaAs), у которого ширина запрещенной зоны равна 1,43 эВ, плотность состояний у дна зоны проводимости
м-3. Определить максимальную рабочую температуруприборов на основе арсенида галлия (GaAs), у которого ширина запрещенной зоны равна 1,43 эВ, плотность состояний у дна зоны проводимости 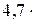 1023 м-3, а у потолка валентной зоны
1023 м-3, а у потолка валентной зоны 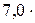 1024 м-3. При этом можно считать, что величины ширины запрещенной зоны и плотностей состояний не зависят от температуры.
1024 м-3. При этом можно считать, что величины ширины запрещенной зоны и плотностей состояний не зависят от температуры.
644. В слиток германия одновременно введены сурьма с концентрацией 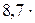 1020 м-3 и галлий с концентрацией
1020 м-3 и галлий с концентрацией 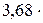 1020м-3. Найти удельную проводимость слитка при условии, что все примесные атомы ионизированы, а подвижность электронов 0,36 м2/(В
1020м-3. Найти удельную проводимость слитка при условии, что все примесные атомы ионизированы, а подвижность электронов 0,36 м2/(В 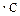 ); сурьма является донором, а галлий – акцептором.
); сурьма является донором, а галлий – акцептором.
645. Образец германия, имеющий при температуре 300 К собственную удельную проводимость 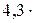 10-4
10-4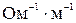 , легирован донорной примесью с концентрацией
, легирован донорной примесью с концентрацией 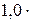 1021 м-3. Найти концентрацию дырок. Определить, какая часть тока обусловлена дырками. Подвижности электронов и дырок при температуре 300 К принять соответственно равными 0,135 м2/(В
1021 м-3. Найти концентрацию дырок. Определить, какая часть тока обусловлена дырками. Подвижности электронов и дырок при температуре 300 К принять соответственно равными 0,135 м2/(В 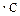 ) и 0,048 м2/(В
) и 0,048 м2/(В 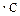 ).
).
646. В чистом германии концентрация собственных носителей при температуре 300 К равна  1019м-3. Подвижности электронов и дырок при этой температуре соответственно равны 0,4 м2/(В
1019м-3. Подвижности электронов и дырок при этой температуре соответственно равны 0,4 м2/(В 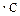 ) и 0,2 м2/(В
) и 0,2 м2/(В 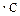 ). Определить проводимость чистого германия и германия с концентрацией акцепторов
). Определить проводимость чистого германия и германия с концентрацией акцепторов 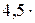 1021 м-3.
1021 м-3.
647. Определить коэффициент амбиполярной диффузии в кремнии при температуре 300 К, если концентрация электронов в Si равна 1011 см-3, а подвижность электронов и дырок соответственно равна 1500 cм2/(В 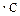 ) и 500 см2/(В
) и 500 см2/(В 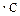 ). Собственная концентрация носителей 1010 см-3.
). Собственная концентрация носителей 1010 см-3.
648. Определить коэффициент амбиполярной диффузии в полупроводнике, если известно, что на расстоянии 0,7 мм от его освещенной поверхности концентрация неравновесных носителей тока спадает в два раза, а время их жизни равно 500 мкс.
649. Коэффициент амбиполярной диффузии в полупроводнике равен 25 см2/c, а время жизни неравновесных носителей тока 200 мкс. Определить концентрацию неравновесных носителей тока на расстоянии 0,5 мм от освещенной поверхности полупроводника, если их концентрация на поверхности 1015 см-3.
650. Подвижность дырок в собственном полупроводнике при температуре 300 К равна 600 см2/(В 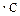 ). Определить подвижность электронов, если коэффициент амбиполярной диффузии равен 30,5 см2/c.
). Определить подвижность электронов, если коэффициент амбиполярной диффузии равен 30,5 см2/c.
651. Определить время жизни неравновесных носителей тока в собственном кремнии при температуре –20 oC, если диффузионная длина равна 2 мм. Подвижности электронов и дырок соответственно равны 1500 см2/(В 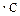 ), 500 cм2/(В
), 500 cм2/(В 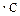 ).
).
652. Образец германия n-типа имеет удельное сопротивление 0,015 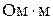 и значение постоянной Холла
и значение постоянной Холла 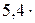 10-3 м3/Кл. Определить концентрацию основных носителей и их подвижность. Дырочной проводимостью пренебречь.
10-3 м3/Кл. Определить концентрацию основных носителей и их подвижность. Дырочной проводимостью пренебречь.
653. Удельная проводимость антимонида индия р-типа 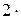 103
103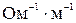 , а подвижность дырок в нем 0,4 м2/(B
, а подвижность дырок в нем 0,4 м2/(B 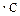 ). Определить постоянную Холла и концентрацию дырок. Электронной проводимостью пренебречь.
). Определить постоянную Холла и концентрацию дырок. Электронной проводимостью пренебречь.
654. Подвижности электронов и дырок в кремнии соответственно равны 0,15 м2/(B 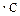 ) и 0,05 м2/(B
) и 0,05 м2/(B 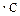 ). Вычислить постоянную Холла для кремния, если его удельное сопротивление 620
). Вычислить постоянную Холла для кремния, если его удельное сопротивление 620 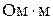 . Кремний рассматривать как собственный полупроводник.
. Кремний рассматривать как собственный полупроводник.
655. Полупроводник в виде тонкой пластины шириной 1 см и длиной 10 см помещен в однородное магнитное поле с индукцией 0,2 Тл. Вектор магнитной индукции перпендикулярен плоскости пластины. К концам пластины приложено постоянное напряжение 300 В. Определить холловскую разность потенциалов на гранях пластины, если постоянная Холла равна 0,1 м3/Кл, а удельное сопротивление – 0,5 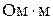 .
.
656. Удельное сопротивление кремния с примесями равно 0,01 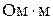 . Определить концентрацию дырок и их подвижность. Принять, что полупроводник обладает только дырочной проводимостью, а постоянная Холла равна
. Определить концентрацию дырок и их подвижность. Принять, что полупроводник обладает только дырочной проводимостью, а постоянная Холла равна  10-4 м3/Кл.
10-4 м3/Кл.
657. р–n-переход находится под обратным напряжением 0,1 В при Т = 300 К. Его сопротивление 692 Ом. Каково сопротивление перехода при прямом напряжении той же величины?
658. Сопротивление p–n-перехода при Т = 300 К, находящегося под прямым напряжением 0,1 В, равно 10 Ом. Определить сопротивление перехода при обратном напряжении.
659. Прямое напряжение, приложенное к p–n-переходу, равно 0,2 В. Вычислить отношение сил тока через переход при температурах 273 К и 300 К. Ширина запрещенной зоны равна 1эВ.
660. Определить, во сколько раз возрастет сила тока насыщения через p–n-переход для кремниевого прибора, если его температура в процессе работы возрастет от 20 оС до 120 оС. Ширину запрещенной зоны для кремния принять равной 1,1 эВ.
661. Определить величину прямого напряжения, при котором ток через p–n-переход равен предельному значению обратного тока (выпрямление отсутствует). Температуру принять равной 20 oC.
ПРИЛОЖЕНИЯ
1. Некоторые физические постоянные (округленные значения)
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
§
Относительные атомные массы некоторых элементов
(округленные значения)
| Элемент | Химический символ | А |
| Азот | N | |
| Аргон | Ar | |
| Водород | H | |
| Гелий | He | |
| Кислород | O | |
| Неон | Ne | |
| Углерод | C |
Масса, заряд и энергия покоя некоторых частиц
| Частица | Масса, кг | Заряд, Кл | Энергия покоя, МэВ |
| Электрон | 9,11 × 10–31 | –1,60 × 10–19 | 0,511 |
| a-частица | 6,64 × 10–27 | 3,2 × 10–19 | |
| Протон | 1,67 × 10–27 | 1,60 × 10–19 |
Относительная диэлектрическая проницаемость
| Вещество | Проницаемость | Вещество | Проницаемость |
| Парафиновая бумага | 2,0 | Масло трансформаторное | 2,2 |
| Стекло | 7,0 | Эбонит | 3,0 |
| Слюда | 7,0 | Резина | 2,5 |
Удельное сопротивление металлов
Показатели преломления
| Вещество | Показатель | Вещество | Показатель |
| Вода | 1,33 | Алмаз | 2,42 |
| Стекло | 1,5 | Кварц | 1,54 |
Работа выхода электрона из металла
| Металл | Работа выхода (Т = 293К); эВ | Металл | Работа выхода (Т = 293К); эВ |
| Золото | 4,3 | Натрий | 2,4 |
| Калий | 2,2 | Платина | 6,3 |
| Литий | 2,3 | Серебро | 4,7 |
| Медь | 4,4 | Цезий | 2,0 |
Электрические характеристики некоторых полупроводников
(температура комнатная)
| Тип полупроводника | Ширина запрещенной зоны | Удельное сопротивление | Подвижность | |
| Еg | Электроны | Дырки | ||
| эВ | 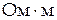 | 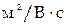 | ||
| Собственный германий | 0,66 | 0,5 | 0,39 | 0,19 |
| Собственный кремний | 1,1 | 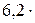 102 102 | 0,15 | 0,05 |
| Арсенид галлия | 1,43 | 0,85 | 0,042 |
Характеристики некоторых радиоактивных изотопов
Массы атомов некоторых химических элементов
Некоторые соотношения между единицами измерения
Физических величин
Множители и приставки для образования десятичных кратных
И дольных единиц и их наименования
| Приставка | Приставка | ||||
| Наименование | Обозначение | Множитель | Наименование | Обозначение | Множитель |
| экса | Э | 1018 | Деци | д | 10–1 |
| пэта | П | 1015 | Санти | с | 10–2 |
| тера | Т | 1012 | Милли | м | 10–3 |
| гига | Г | 109 | Микро | мк | 10–6 |
| мега | М | 106 | Нано | н | 10–9 |
| кило | К | 103 | Пико | п | 10–12 |
| гекто | Г | 102 | Фемто | ф | 10–15 |
| Дека | Да | 101 | Атто | а | 10–18 |
Греческий алфавит
| Обозначения букв | Названия букв | Обозначения букв | Названия букв |
| A,a | альфа | N,n | ню |
| B,b | бета | X,x | кси |
| G,g | гамма | O,o | омикрон |
| Δ,d | дельта | P,p | пи |
| E,e | эпсилон | R,r | ро |
| Z,z | дзета | S,s | сигма |
| H,h | Эта | T,t | тау |
| Q,q | тхэта | U,u | ипсилон |
| I,i | йота | F,j | фи |
| K,k | каппа | C,c | хи |
| L,l | ламбда | Y,y | пси |
| M,m | мю | W,w | омега |
СОДЕРЖАНИЕ
Стр.
ВВЕДЕНИЕ…………………………………………………………………………………………….. 3
1. ОБЩИЕ ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ КОНТРОЛЬНЫХ РАБОТ… 3
Библиографический список……………………………………………………………………… 5
2. КОНТРОЛЬНАЯ РАБОТА № 1 “ФИЗИЧЕСКИЕ ОСНОВЫ
МЕХАНИКИ”………………………………………………………………………………………….. 7
2.1. Методические указания к выполнению контрольной работы № 1……….. 7
2.2. Основные законы и формулы. Примеры решения задач………………………. 10
2.2.1. Кинематика поступательного и вращательного движения………………… 10
Примеры решения задач…………………………………………………………………………… 11
2.2.2. Динамика. Законы Ньютона…………………………………………………………….. 13
Примеры решения задач…………………………………………………………………………… 14
2.2.3. Работа постоянной и переменной силы.
Закон сохранения механической энергии…………………………………………………… 16
Примеры решения задач…………………………………………………………………………… 17
2.2.4. Закон сохранения импульса. Совместное применение законов
сохранения импульса и механической энергии………………………………………….. 20
Примеры решения задач…………………………………………………………………………… 21
2.2.5. Динамика вращательного движения твёрдого тела…………………………… 23
Примеры решения задач…………………………………………………………………………… 24
2.2.6. Закон сохранения момента импульса. Кинетическая энергия
вращающегося тела………………………………………………………………………………….. 25
Примеры решения задач…………………………………………………………………………… 27
2.2.7. Элементы специальной теории относительности……………………………… 29
Примеры решения задач…………………………………………………………………………… 30
2.3. Задание на контрольную работу № 1………………………………………………….. 31
3. КОНТРОЛЬНАЯ РАБОТА № 2 “МОЛЕКУЛЯРНАЯ ФИЗИКА. ОСНОВЫ
ТЕРМОДИНАМИКИ”……………………………………………………………………………… 41
3.1. Методические указания к выполнению контрольной работы № 2……….. 41
3.2. Основные законы и формулы. Примеры решения задач……………………….43
3.2.1. Идеальный газ, уравнение состояния идеального газа
(уравнение Клапейрона-Менделеева)………………………………………………. 43
Примеры решения задач………………………………………………………………………….. 44
3.2.2. Основное уравнение молекулярно-кинетической теории газов.
Внутренняя энергия идеального газа………………………………………………. 46
Примеры решения задач………………………………………………………………………….. 47
3.2.3. Элементы классической статистики………………………………………………… 49
Примеры решения задач………………………………………………………………………….. 50
3.2.4. Первое начало термодинамики. Теплоёмкость идеального газа……….. 52
Примеры решения задач………………………………………………………………………….. 53
3.2.5. Круговые процессы. КПД цикла. Цикл Карно…………………………………. 56
Примеры решения задач………………………………………………………………………….. 56
3.2.6. Энтропия……………………………………………………………………………………….. 57
Примеры решения задач…………………………………………………………………………. 57
3.3. Задание на контрольную работу № 2………………………………………………… 59
4. КОНТРОЛЬНАЯ РАБОТА № 3 “ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ”.. 68
4.1. Методические указания к выполнению контрольной работы № 3……… 68
4.2. Основные законы и формулы. Примеры решения задач…………………….. 71
4.2.1. Электростатика……………………………………………………………………………… 71
Примеры решения задач…………………………………………………………………………. 75
4.2.2. Постоянный электрический ток……………………………………………………… 83
Примеры решения задач…………………………………………………………………………. 84
4.2.3. Магнитостатика…………………………………………………………………………….. 87
Примеры решения задач…………………………………………………………………………. 89
4.2.4. Электромагнитная индукция………………………………………………………….. 97
Примеры решения задач…………………………………………………………………………. 98
4.3. Задание на контрольную работу № 3…………………………………………………. 102
5. КОНТРОЛЬНАЯ РАБОТА № 4 “КОЛЕБАНИЯ И ВОЛНЫ”………………… 114
5.1. Методические указания к выполнению контрольной работы № 4………. 114
5.2. Основные законы и формулы. Примеры решения задач…………………….. 116
5.2.1. Гармонические механические колебания……………………………………….. 116
Примеры решения задач…………………………………………………………………………. 117
5.2.2. Затухающие колебания………………………………………………………………….. 118
Примеры решения задач…………………………………………………………………………. 119
5.2.3. Электромагнитные колебания………………………………………………………… 120
Примеры решения задач………………………………………………………………………….. 121
5.2.4. Сложение гармонических колебаний………………………………………………. 122
Примеры решения задач………………………………………………………………………….. 123
5.2.5. Упругие и электромагнитные волны……………………………………………….. 125
Примеры решения задач………………………………………………………………………….. 125
5.2.6. Интерференция света………………………………………………………………………. 126
Примеры решения задач…………………………………………………………………………… 128
5.2.7. Дифракция света…………………………………………………………………………….. 130
Примеры решения задач………………………………………………………………………….. 132
5.2.8. Поляризация света………………………………………………………………………….. 135
Примеры решения задач………………………………………………………………………….. 136
5.3. Задание на контрольную работу № 4…………………………………………………. 137
6. КОНТРОЬНАЯ РАБОТА № 5 “КВАНТОВАЯ ФИЗИКА”…………………….. 149
6.1.Методические указания к выполнению контрольной работы № 5……….. 149
6.2. Основные законы и формулы. Примеры решения задач……………………… 151
6.2.1. Тепловое излучение………………………………………………………………………… 151
Примеры решения задач………………………………………………………………………….. 151
6.2.2. Фотоэффект……………………………………………………………………………………. 152
Примеры решения задач………………………………………………………………………….. 153
6.2.3. Физика атома. Спектры атомов……………………………………………………….. 154
Примеры решения задач…………………………………………………………………………. 155
6.2.4. Элементы квантовой механики……………………………………………………….. 156
Примеры решения задач………………………………………………………………………….. 157
6.2.5. Физика твёрдого тела……………………………………………………………………… 162
Примеры решения задач………………………………………………………………………….. 162
6.2.6. Физика атомного ядра. Радиоактивность…………………………………………. 165
Примеры решения задач…………………………………………………………………………… 166
6.3. Задание на контрольную работу № 5………………………………………………….. 170
7. КОНТРОЛЬНАЯ РАБОТА № 6 “ФИЗИКА ТВЁРДОГО ТЕЛА”……………. 179
7.1. Методические указания к выполнению контрольной работы № 6………. 179
7.2. Основные законы и формулы. Примеры решения задач……………………… 180
7.2.1. Пространственная решётка кристалла…………………………………………….. 180
Примеры решения задач………………………………………………………………………….. 183
7.2.2. Теплоёмкость и теплопроводность кристаллов……………………………….. 185
Примеры решения задач………………………………………………………………………….. 186
7.2.3. Электронный газ в металлах…………………………………………………………… 188
Примеры решения задач………………………………………………………………………….. 189
7.2.4. Соственные и примесные полупроводники……………………………………… 190
Примеры решения задач………………………………………………………………………….. 192
7.2.5. р – n-переход. Диффузия носителей тока………………………………………… 193
Примеры решения задач………………………………………………………………………….. 194
7.2.6. Эффект Холла………………………………………………………………………………… 195
Примеры решения задач………………………………………………………………………….. 196
7.3. Задания на контрольную работу № 6…………………………………………………. 197
ПРИЛОЖЕНИЯ………………………………………………………………………………………. 206
Валентина Павловна Дзекановская
Елена Андреевна Лиходаева
Инна Георгиевна Орехова
Наталья Анатольевна Тупицкая
Валентина Борисовна Харламова
Юрий Валентинович Чуркин
Дмитрий Георгиевич Летенко
Сергей Васильевич Субботин
Физика
Задания на контрольные работы.
Методические указания к выполнению контрольных работ
Редактор
Сводный темплан 2009 г.
Лицензия ЛР N 020308 от 14.02.97.
Санитарно-эпидемиологическое заключение № 78.01.07.953.П.005641.11.03
Подписано в печать Формат 60 х 84 1/16
Б. кн. — журн. П. л. Б.л. Изд-во СЗТУ
Заказ
Северо-Западный государственный заочный технический университет
Издательство СЗТУ, член Издательско-полиграфической ассоциации университетов России
191186, Санкт-Петербург, ул. Миллионная, 5
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Следствия из основного уравнения мкт идеального газа
Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):
v=√3kTm0..=√3RTM..
R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:
R=NAk=8,31 Дж/К·моль
Температура — мера кинетической энергии молекул идеального газа:
−Ek=32..kT
T=2−Ek3k..
Полная энергия поступательного движения молекул газа определяется формулой:
E=N−Ek
Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?
Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:
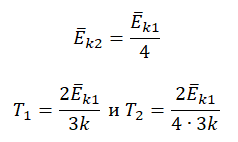
Следовательно:
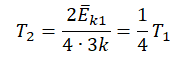
Составим систему уравнений:
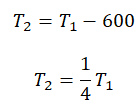
Отсюда:
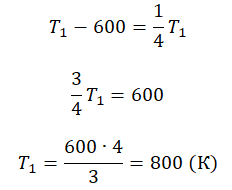
Кислород
Электронная конфигурация невозбужденного атома кислорода 1s22s22р4:

Подобно фтору, кислород образует соединения почти со всеми элементами (кроме гелия, неона и аргона). Поскольку по электроотрицательности кислород уступает только фтору, степень окисления кислорода в подавляющем большинстве соединений равна —2. Кроме того, кислород проявляет степени окисления 2 и 4, а также 1 и –1 в соединениях со связью О—О.
Кислород — самый распространенный элемент (58,0 мол. доли) на Земле. Состоит из трех стабильных изотопов: 16О (99,759%), 17О (0,037%) и 18O (0,204%). Искусственно получены также изотопы 14O, 15O и 19О, период полураспада которых исчисляется десятками секунд. Вследствие количественного преобладания и большой окислительной активности кислород предопределяет форму существования на Земле всех остальных элементов. Его значение было особенно велико в период образования земной коры. Предполагается, что наличие кислорода в атмосфере обусловлено вторичными процессами деятельностью зеленых растений.
Простые вещества. Наиболее устойчива двухатомная молекула кислорода О2. Как показывают магнитные исследования, она парамагнитна. При этом величина ее парамагнетизма отвечает наличию двух непарных электронов:
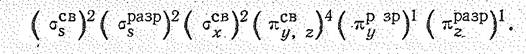

В молекуле О2 на 8 связывающих электронов приходится 4 разрыхляющих, поэтому порядок связи в ней равен двум. Учитывая парамагнетизм и порядок связи, строение молекулы О2 можно передать структурными формулами[1]:

Вследствие кратности связи межатомное расстояние в О2 (0,1207 нм) меньше длины одинарной связи 0—О (0,148 нм). По этой же причине молекула О2 весьма устойчива, ее энергия диссоциации равна 494 кДж/моль, в то время как энергия одинарной связи О–О всего 210 кДж/моль. Диссоциация молекул О2 на атомы становится заметной лишь при 2000°С; она имеет место также при поглощении ультрафиолетового излучения (фотолиз).
Температуры плавления (—218,9 °С) и кипения (—183 °С) кислорода очень низкие. Он плохо растворяется в воде (5 объемов О2 в 100 объемах Н2О при 0 °С). Жидкий и твёрдый кислород притягивается магнитом.
Аллотропическую модификацию кислорода озон О3 можно рассматривать как соединение О (IV).
Кислород обладает высокой химической активностью, особенно при нагревании и в присутствии катализатора; с большинством простых веществ он взаимодействует непосредственно, образуя оксиды; лишь по отношению к фтору проявляет восстановительные свойства.
Кислород получают ректификацией жидкого воздуха, а также как побочный продукт при электролизе воды. В лаборатории для его получения используют термическое разложение богатых кислородом соединений (КМnО4, КСlO3 и др.).
Соединения со степенью окисления кислорода —2. Как уже указывалось, образование двух- и многозарядных одноатомных анионов Эn— энергетически невыгодно. Поэтому не существует соединений, содержащих ион О2-. Даже в кристаллических оксидах наиболее активных металлических элементов типа Nа2O и СаО эффективный заряд атома кислорода составляет всего около 1—.
Как и для других р-элементов 2-го периода, максимальная валентность (число двухэлектронных двухцентровых связей) кислорода равна четырем. При этом атомы кислорода могут находиться в состоянии sр3-, sр2— и sр-гибридизации, что соответствует тетраэдрическому, треугольному и линейному расположению s–связей. В качестве примера соединений, в которых проявляются эти гибридные состояния орбиталей кислорода, можно указать соответственно кристаллические ВeО, ТiO2 и SiO2.
Весьма разнообразны также оксиды, в которых координационное число кислорода превышает значение его максимальной валентности, т. е. больше четырех. Например, в кристалле МgO координационное число кислорода равно шести, а в кристалле Nа2O восьми. Согласно теории молекулярных орбиталей это обусловлено тем, что в кристалле MgO (структурный тип NаСI) каждый атом О (за счет 2pх-, 2рy— и 2рz-орбиталей) объединяется с шестью соседними атонами Мg посредством трех трехцентровых связей. Аналогично построены кристаллические МnО, FеО, СоО, NiO и другие оксиды со структурой типа NаСI.
В оксидах типа Nа2O (К2O, Rb2O, Li2O) атомы кислорода (за счет 2s, 2рx-, 2pу— и 2рz-орбиталей) с восемью соседними атомами металла объединяются посредством четырех трехцентровых связей.
Состав кристаллических оксидов (в особенности d-элементов) в большей или меньшей степени переменный. Так, для МnО он изменяется в пределах от МnО до МnО1.5, а для МnО2 — от МnO1,5 до МnО2,6. Если в оксидах содержание кислорода выше стехиометрического, они проявляют дырочную проводимость, а если содержание металла выше стехиометрического, то электронную. Полупроводниками с дырочной проводимостью являются МnО, Сu2О, FеО н др. Ряд оксидов, состав которых не подчиняется обычным правилам степеней окисления (например, Сr3О, Тi6О, Тi3О), — металлические соединения.
Важнейшим из оксидов является оксид водорода — вода. Достаточно сказать, что она составляет 50—99% массы любого живого существа. Кровь человека содержит более 4/5 воды, мускулы — 35% воды. При средней продолжительности жизни (70 лет) человек выпивает около 25 т воды.
Молекула воды имеет угловую форму, что согласно теории валентных связей соответствует sр3-гибридвому состоянию атома кислорода. В молекуле Н2O две sр3-гибридные орбитали атома кислорода участвуют в образовании двух связей О—Н. На двух других sр3-гибридных орбиталях расположены две несвязывающие электронные пары. Валентный угол в молекуле воды НOН составляет 104,5о.
В рамках теории молекулярных орбиталей модель молекулы воды соответствует распределению восьми валентных электронов по двум связывающим и двум несвязывающим молекулярным орбиталям
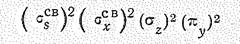
и наличию двух свободных разрыхляющих орбиталей (рис. 1). Такое объяснение подтверждается наличием у молекулы Н2О четырех первых потенциалов ионизации (27,3; 16,2; 14,5 и 12,6 эВ).
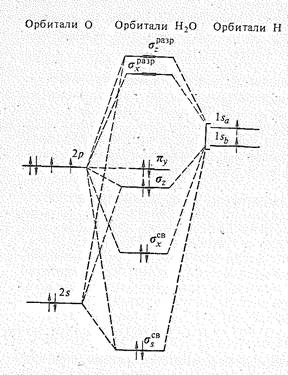 С позиций теории молекулярных орбиталей строение молекулы Н2О можно объяснить следующим образом. Взаимное расположение атомов водорода и кислорода в молекуле воды можно представить схемой:
С позиций теории молекулярных орбиталей строение молекулы Н2О можно объяснить следующим образом. Взаимное расположение атомов водорода и кислорода в молекуле воды можно представить схемой:
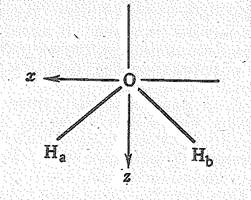
Рис 1. Энергетическая Молекулярные орбитали Н2О образуются за счет 2s-,
диаграмма орбиталей и 2р-орбиталей атома кислорода и 1s-орбиталей
молекулы Н2О двух атомов водорода. Характер перекрывания этих
орбиталей показан на рис. 2.
Перекрывание 2рx-орбитали атома кислорода и 1s-орбиталей двух атомов водорода приводит к возникновению молекулярных sxсв.— и sхразр.-орбиталей, Как видно из рис. 2, характер перекрывания 2s— и 2рz-орбиталей кислорода одинаков. В результате образуются три молекулярные орбитали: связывающая ssсв., почти несвязывающая sz и разрыхляющая szразр.. Орбиталь 2рy, расположенная перпендикулярно плоскости расположения атомов Н и О, с 1s-орбиталями атомов Н не перекрывается и в молекуле Н2O играет роль не-связывающей молекулярной py -орбитали.
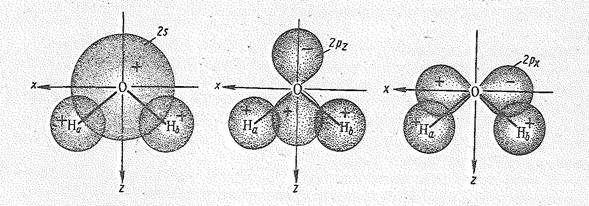
Рис. 2. Перекрывание 2s-, 2рz— и 2рx-орбиталей атома кислорода с 1s-орбиталями двух атомов водорода молекулы воды.
Таким образом, комбинация исходных четырех атомных орбиталей кислорода и двух орбиталей атомов водорода приводит к образованию двух связыазющнх (ssсв. и sxсв.), двух несвязывающих (sz и py) и двух разрыхляющих (sxразр. И szразр.) молекулярных орбиталей (см. рис. 1).
В соответствии с природой элемента в положительной степени окисления характер оксидов в периодах и группах периодической системы закономерно изменяется. В периодах уменьшается отрицательный эффективный заряд на атомах кислорода dо и осуществляется постепенный переход от основных через амфотерные оксиды к кислотным, например:
 Различие в свойствах оксидов разного типа проявляется при их взаимодействии с водой:
Различие в свойствах оксидов разного типа проявляется при их взаимодействии с водой:

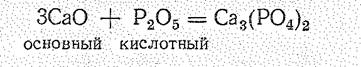 а также при взаимодействии оксидов разного типа друг с другом:
а также при взаимодействии оксидов разного типа друг с другом:
Амфотерные оксиды с водой не взаимодействуют, но могут реагировать и с кислотами, и с щелочами:
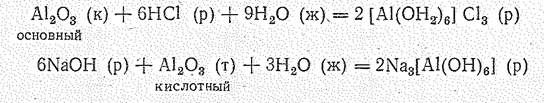
а при сплавлении — с основными и кислотными оксидами.
Сравнительную количественную оценку основно-кислотной активности оксидов можно дать на основании значений DG соответствующих однотипных реакций. Уменьшение отрицательного значения DGо298 в реакциях

свидетельствует об ослаблении в ряду Nа2О – МgО —Al2O3 их основных свойств, а также об их способности взаимодействовать с водой. В ряду Р2О5—SO3—Сl2О7
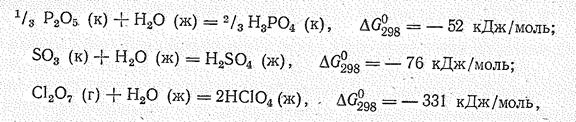
наоборот, наблюдается увеличение отрицательного значения DGо298, что свидетельствует об усилении у оксидов кислотных свойств.
Соединения перекисного типа. Сродство к электрону молекулы O2 составляет 0,8 эВ, а ее энергия ионизации 12,08 эВ. При химических превращениях молекула O2 может присоединять или терять электроны с образованием молекулярных ионов типа O22-, O2— и O2 (табл. 1).
Таблица 1.
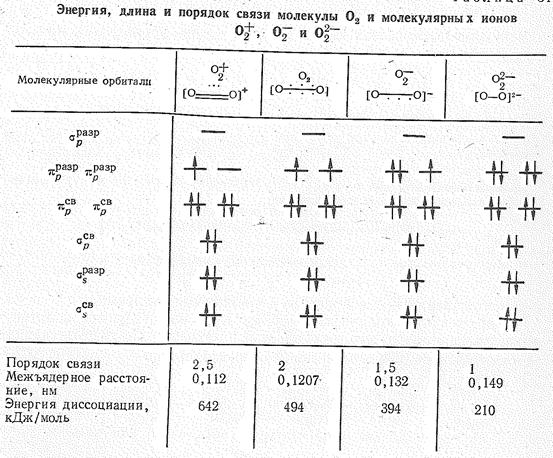
Как видно из табл. 1, удаление электрона с pразр. -орбитали молекулы О2 соответствует повышению порядка связи в О2 , а появление электронов на pразр -орбитали приводит, наоборот, к уменьшению порядка связи в молекулярных нонах О22- и О2—. В соответствии с этим в ряду О2 – О2 — О2— — О22- расстояние между атомами кислорода увеличивается, а средняя энергия связи уменьшается.
Присоединение одного электрона к молекуле О2 вызывает образование надпероксид— нона О2— :
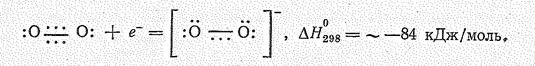
Производные радикала О2— называются надпероксидами; они известны для наиболее активных щелочных металлов (К, Rb, Сs). Надпероксиды образуются при прямом взаимодействии простых веществ:
К O2 = КO2.
Непарный электрон нона О2— обусловливает парамагнетизм надпероксидов и наличие у них окраски. Надпероксиды — очень сильные окислители. Oни бурно реагируют с водой с выделением кислорода.
Присоединяя два электрона, молекула О2 превращается в пероксид-ион О22-, в котором атомы связаны одной двухэлектронной связью, и поэтому он диамагнитен:

Это также согласуется с отсутствием окраски у пероксидов,
Пероксиды образуются при окислении ряда металлов, например:
Ва О2 = ВаО2
Наибольшее практическое значение имеет пероксид (перекись) водорода Н2О2. Строение молекулы показано ниже:
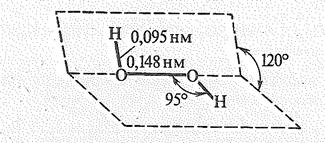
Энергия связи О — О (210 кДж/моль) почти в два раза меньше энергии связи О — Н (468 кДж/моль).
Из-за несимметричного распределения связей Н – О молекула Н2О2 сильно полярна ( = 0,7. 10-29 Кл×м). Между молекулами Н2О2 возникает довольно прочная водородная связь, приводящая к их ассоциации. Поэтому в обычных условиях пероксид водорода — сиропообразная жидкость (пл. 1,44) с довольно высокой температурой кипения (т. кип. 150,2 °С, т. пл. 0,41 °С). Она имеет бледно-голубую окраску. Пероксид водорода — хороший. ионизирующий растворитель. С водой смешивается в любых отношениях благодаря возникновению новых водородных связей. Из растворов выделяется в виде неустойчивого кристаллогидрата Н2О2×2Н2О (т. пл. —52,0 °С). В лаборатории обычно используются 3%-ные и 30%-ные растворы Н2О2 (последний называют пергидролем).
В водных растворах пероксид водорода — слабая кислота (Киониз = 2,24×10-12):

В химических реакциях пероксид-радикал может, не изменяясь, переходить в другие соединения, например:
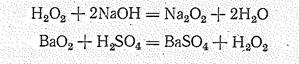
Последняя реакция используется для получения перекиси водорода.
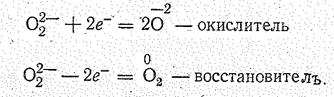 Чаще, однако, протекают реакции, сопровождающиеся разрушением связи О — О или изменением заряда иона О22-. Можно считать, что ион О присоединяет или теряет электроны:
Чаще, однако, протекают реакции, сопровождающиеся разрушением связи О — О или изменением заряда иона О22-. Можно считать, что ион О присоединяет или теряет электроны:
Окислительные свойства пероксидов выражены сильнее, чем восстановительные:
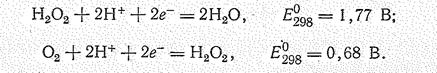
Так, при действии концентрированных растворов Н2О2 на бумагу, опилки или другие горючие вещества происходит их самовоспламенение. Восстановительные свойства перекись водорода проявляет только по отношению к таким сильным окислителям, как ионы МnО4—.
Для пероксида водорода характерен также распад по типу диспропорционирования:
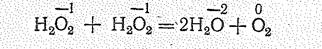
Этот распад ускоряется в присутствии примесей, при освещении, нагревании и может протекать со взрывом. Довольно устойчивы только очень чистая Н2О2 и ее 30—65%-ные растворы. Пероксид водорода и его растворы обычно хранят в темной посуде и на холоде; для стабилизации добавляют ингибиторы.
Водные растворы пероксида водорода широко используются для отбелки различных материалов, для обеззараживания сточных вод. Пероксид водорода применяют как окислитель ракетного топлива.
В последнее время удалось синтезировать Н2О3 и Н2О4. Эти соединения весьма неустойчивы. При обычных температурах они разлагаются за доли секунды. Однако при низких температурах порядка —70°С они существуют часами. Спектроскопическое исследование показывает, что их молекулы имеют зигзагообразную цепную структуру:

Молекулы Н2О2, как и Н2О, могут выступать в качестве нейтральных лигандов, например [Fе(ОН2)5(О2Н2)]3 , и давать аналогичные кристаллогидратам пероксогидраты: К2СО3 ×3Н2O2, СаО2×2Н2O2, ВаO2×2Н2О×2Н2О2 и др. Роль лиганда может играть и пероксидион, например в комплексе [V(О2)4]3-:
Кислоты, в которых имеется группировка О22-, называют пероксокислотами:
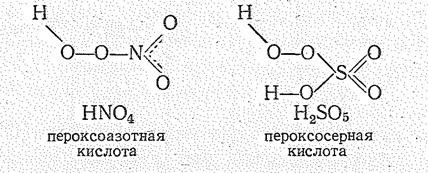
При гидролизе пероксокислот образуется пероксид водорода, что используется для его получения в промышленности.
Характерным свойством пероксидных соединений, как простых, так и комплексных, является способность образовывать пероксид водорода при взаимодействии с разбавленными растворами кислот, а также выделять кислород при термическом разложении или действии воды и других химических агентов. Другие неорганические соединения, которые могут быть источником кислорода, как, например, нитраты, хлораты, перхлораты, перманганаты и некоторые оксиды, не выделяют пероксид водорода при действии воды. Кислород они выделяют только при нагревании и в присутствии катализаторов.
Соединения кислорода (II) и кислорода (I). Можно считать, что электроположительная поляризация атомов кислорода проявляется в соединениях с фтором, а также в ионе О2 . Некоторые примеры фторопроизводных кислородных соединений приведены в табл. 2.
Простейший представитель такого рода соединений — дифторид кислорода ОF2: его получают при быстром пропускании фтора через 2%-ный раствор щелочи:
2F2 2NaOH = OF2 2NaF H2O
Таблица 2.
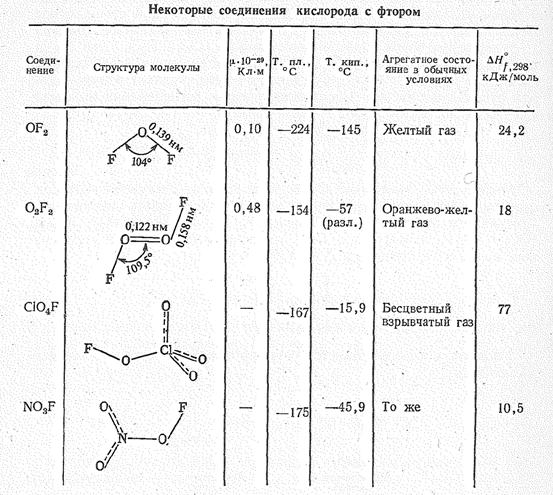
Молекула ОF2 имеет угловую форму (dOF = 0,139 нм, ÐFОF = 104° 16’, m= 0,1 × 10-29 Кл×м.) Дифторид кислорода ядовитый газ бледно-желтого цвета, термически устойчив до 200—250 °С, сильный окислитель, эффективный фторирующий агент.
В диоксидифториде О2F2 радикал О22 ковалентно связан с атомами фтора. Молекула О2F2 диамагнитна. Это соединение образуется (в виде красной летучей жидкости) в результате непосредственного взаимодействия простых веществ в электрическом разряде или под действием ионизирующих излучений при температуре жидкого воздуха (—190 °С). Согласно спектроскопическим данным молекула О2F2 (m = 0,48×10-29 Кл×м) по структуре аналогична Н2О2:
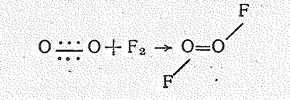
Соединение крайне неустойчиво, что определяется низкой энергией разрыва связи ОF (75 кДж/моль).
Получены также полиоксидифториды типа О4F2, О5F2 и О6F2, существующие лишь при низкой температуре (—190 °с). Предполагают, что их молекулы имеют цепное строение, например F—О—О—О—О—F. Термическая устойчивость полиоксидифторидов уменьшается с увеличением числа атомов в молекуле ОnF2 (n = 2 – 6).
Энергия ионизации молекулы О2 довольно значительная (12,08 эВ), однако при взаимодействии О2 с сильнейшим окислителем РtF6 образуется солеподобное вещество О2 [РF6]—
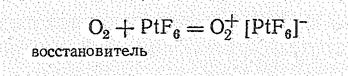
в котором роль катиона играет молекулярный ион О2 (диоксигенил):

Гексафтороплатинат (V) диоксигенила О2[РtF6] – парамагнитное вещество красного цвета, плавится с разложением при 219 °С. Синтез этого соединения канадским ученым Н. Бартлетом в 1962 г. послужил толчком к синтезу соединений ксенона, энергия ионизации которого близка к таковой молекулы кислорода.
Производные О2 получены также при взаимодействии O2F2 и O4F2 с резко кислотными фторидами типа ВF3, РF5, AsF5, SbF5, ВrF5:
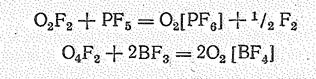
Синтез диоксигенильных солей можно осуществлять нагреванием в автоклаве (в течение 10—20 ч) при 150—500 °С смеси кислорода, фтора и порошка соответствующего металла:
О2 3 F2 Э = O2[ЭF6]
где Э – As, Sb, Bi, Nb, Au, Ru, Rh.
Частота валентных колебаний О2 в диоксигенильных соединениях близка к таковой для свободного иона, что подтверждает существование иона О2 в указанных солях. Межъядерное расстояние в катионе О2 , известное из спектроскопических данных (0,112 нм), как и следовало ожидать, короче, чем в О2 0,1207 нм). Ион О2 имеет один непарный электрон (см. табл. 1). Энергия диссоциации О2F2, ОF2 (~70 кДж/моль) меньше, чем у F2 (159 кДж/моль). Они — удобная форма хранения фтора, который выделяется при распаде этих фторидов уже при обычных температурах.
В соединениях типа СlО4F, NO3F мостиковый атом кислорода относительно центрального атома (Сl, N) поляризован отрицательно, а относительно атома фтора — положительно. Рассматриваемые соединения можно получить при взаимодействии с фтором концентрированных растворов НСlО4 и НNO3 или твердых солей КСlО4 и KNO3
HClO4 F2 = ClO4F HF
KNO3 F2 = NO3F KF
В воде эти соединения разлагаются, выделяя кислород:
ClO4F 2Н2О = HClO4 O2 2HF
Производные положительной степени окисления кислорода являются сильнейшими энергоемкими окислителями, способными выделять запасенную в них химическую энергию в определенных условиях. Их можно использовать как эффективные окислители ракетного топлива.
Соединения кислорода (IV). В качестве производного, в котором кислород проявляет степень окисления 4, можно рассматривать аллотропическую модификацию кислорода озон O3 – (О 4O2).
Молекула O3 диамагнитна, имеет угловую форму (ÐООО = 116,5°) и обладает некоторой полярностью (m = 0,17 × 10-29 Кл × м). Длина связи dOO ( 0,128 нм) является промежуточной между длиной одинарной (0,149 нм) и двойной связи (0,1207 нм). Поэтому считают, что в молекуле О3 порядок связи 1,5. Строение молекулы О3 можно передать следующей структурной формулой:
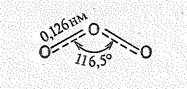
Исходя из приведенных данных, строение молекулы О3 можно объяснить следующим образом. Центральный атом кислорода молекулы О3 находится в состоянии sр2-гибридизации (за счет 2s-, 2pх н 2рy,-орбиталей). Две из гибридных sр2-орбиталей центрального атома участвуют в образовании двух s-связей О—О (двух молекулярных sсв.-орбиталей). Третья sр2-гибридная орбиталь (молекулярная s-орбиталь) содержит неподеленную электронную пару. 2рz -орбиталъ центрального атома (расположенная перпендикулярно плоскости расположения атомов) и 2рz-орбитали крайних атомов участвуют в образовании нелокализованной p-связи (молекулярная pсв.-орбиталь). Таким образом, невозбужденное состояние молекулы О3 отвечает следующему заполнению молекулярных орбиталей: (sсв.)4(pсв.)2(s)2.
Остальные электроны заполняют несвязывающие орбитали, локализованные у периферических атомов.
Шести электронам, связывающим три атома кислорода, соответствует порядок связи 1,5.
Озон газ синего цвета с резким раздражающим запахом, очень токсичен. Жидкий озон — темно-синяя жидкость, твердый – темно- фиолетовые кристаллы (т. пл. —192,7 °С). Поскольку молекула О3 обладает большей полярностью и поляризуемостью, озон имеет более высокую температуру кипения (—111,9 °С), чем кислород. Этим же объясняется большая интенсивность окраски озона и лучшая его растворимость в воде.
Озон образуется в процессах, сопровождающихся выделением атомарного кислорода (радиолиз воды, разложение перекисей и др.), а также при действии на молекулярный кислород потока электронов, протонов, коротковолнового излучения, т. е. за счет радиохимических
и фотохимических реакций. Цепную реакцию образования озона из кислорода можно представить схемой
О2 hn ® O2·
O2· O2 = O3 ·O·
·O· O2 = O3
или суммарно 3О2 = 2О3 DGо298 = 326 кДж/моль.
В естественных условиях озон образуется из атмосферного кислорода при грозовых разрядах, а на высоте 10—30 км — под действием ультрафиолетовых солнечных лучей. Озон задерживает вредное для жизни ультрафиолетовое излучение Солнца и поглощает инфракрасное излучение Земли, препятствуя ее охлаждению. Следовательно, «озонный пояс» играет большую роль в обеспечении жизни на Земле.
В технике озон получают в озонаторах действием тихого электрического разряда на кислород.
Озон — вещество эндотермическое (DНof,298 = 142,3 кДж/моль, DGof,298 = 162,7 кДж/моль). Но тем не менее в отсутствие катализаторов или без ультрафиолетового облучения газообразный озон разлагается довольно медленно даже при 250 °С. Жидкий озон и его концентрированные смеси (70% 0) взрывчаты.
Окислительная активность озона заметно выше, чем О2. Например, уже при обычных условиях он окисляет многие малоактивные простые вещества (Аg, Нg и пр.):
8Аg 2O3 = 4Аg2О O2
О более высокой химической активности О3, чем O2, свидетельствует также сравнение их окислительно-восстановительных потенциалов для водных растворов, например:
О3 (г) Н2О (ж) 2е— = О2 (г) 2ОН— (р), Ео298 = 1,24 В;
О2 (г) 2Н2О (ж) 4е— = 4ОН— (р), Ео298 = 0,401 В.
Для количественного определения озона можно использовать его взаимодействие с раствором КI:
2I— (р) O3 (г) Н2O (ж) = I2 (т) 2ОН— (р) О2 (г)
Сродство к электрону озона около 180 кДж/моль, поэтому он может переходить в озонид-ион О3—. В частности, при действии озона на щелочные металлы образуются озониды: К О3 = КО3
Озониды — это соединения состоящие из положительных ионов металла и отрицательных ионов О3— (dOO = 0,134 нм). Наличие в ионе О3— непарного электрона обусловливает парамагнетизм и наличие окраски у озонидов, Обычно они окрашены в красный цвет.
Как сильный окислитель озон используется для очистки питьевой воды, для дезинфекции воздуха, в различных химических синтезах.
[1] Тремя точками обозначены связи, обусловленные двумя pсв. и одним pразр. электроном, что отвечает порядку связи 0,5. Во второй формуле непарные точки означают pразр.-электроны, При возбуждении молекул О2 становится диамагнитной. Этому состоянию отвечает структурная формула .
§
Т 4 Л 10 Подгруппа мышьяка
Мышьяк Аs, сурьма Sb и висмут Вi — полные электронные аналоги с конфигурацией s2р3. По мере увеличения размеров атомов в ряду Аs — Sb — Вi значения устойчивых координационных чисел возрастают. Степени окисления мышьяка, сурьмы и висмута равны —3, 3 и 5. Вследствие особой устойчивости конфигурации 6s2 для висмута наиболее характерна степень окисления 3.
Содержание в земной коре мышьяка, сурьмы и висмута сравнительно невелико. Они обычно встречаются в виде сульфидных минералов:
Простые вещества. В ряду N—Р—Аs—Sb—Вi отчетливо наблюдается усиление металлических признаков простых веществ.
В частности, в этом ряду устойчивость неметаллических модификаций падает, а металлических возрастает. Мышьяк, как и фосфор, имеет несколько аллотропных форм. При быстром охлаждении пара (состоящего из молекул As4) образуется неметаллическая модификация — желтый мышьяк (пл. 2,0 г/см3), изоморфный белому фосфору и подобно ему растворимый в сероуглероде. Эта модификация менее устойчива, чем белый фосфор, и при действии света или при слабом нагревании легко переходит в металлическую модификацию — серый мышьяк. Неметаллическая модификация сурьмы (желтая сурьма) еще менее устойчива, чем желтый мышьяк. У висмута же неметаллическая модификация неизвестна вообще.
Устойчивые в обычных условиях модификации — серый мышьяк, серая сурьма и висмут — имеют металлический вид, электропроводны, но хрупки. Они изоморфны, имеют слоистую структуру типа черного фосфора. Каждый из атомов пирамидально связан с тремя соседними по слою и имеет трех ближайших соседей в другом слое. В ряду As—Sb—Вi различие межъядерных расстояний внутри и между слоями уменьшается (0,063—0,050—0,0З7 нм), т. е. происходит постепенно приближение к характерному для металлических структур равенству межъядерных расстояний. Благодаря близости параметров кристаллических решеток сурьма образует твердые растворы с мышьяком и висмутом, но последние друг с другом их не образуют.
Некоторые сведения о простых веществах р-элементов V группы приведены ниже: ( в твердом состоянии; При 1,8×109 Па; При 3,6×106 Па.)

В обычных условиях металлические модификации устойчивы по отношению к воздуху и воде. В ряду напряжений они располагаются после водорода. При взаимодействии с концентрированной НNО3 мышьяк переходит в мышьяковую кислоту:
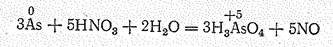
Сурьма в этих же условиях образует b-сурьмяную кислоту НSbO3 (Sb2О5× nН2О):
3Sbo 5HNO3 = 3НSb 5O3 5NO Н2О
Висмут же в концентрированной НNО3 пассивируется, а с разбавленной дает нитрат, т. е. ведет себя как металл:
Вio 4HNO3 = Вi 3(NO3)3 NО 2Н2О
Для получения мышьяка, сурьмы и висмута их природные сульфиды обжигают; образующиеся при этом оксиды восстанавливают углем:
2Э2S3 9O2 = 6SO2 2Э2O3
Э2O3 3С = 2Э 3СО
Мышьяк, сурьма и висмут существенно отличаются по структуре от типичных металлов и поэтому с металлами твердые растворы обычно не образуют. Более характерно возникновение эвтектических смесей. Так, сплав состава 60% Вi и 40% Сd плавится при 144 °С. Широко применяемый сплав Вуда, температура плавления которого 65 – 70 °С, т. е. ниже точки кипения воды, содержит 50 % Вi, 25 % Рb, 12,5 % Sn и 12,5 % Сd. Сплав состава 41 % Вi, 22 % Рb, 11 % Sn, 8 % Сd и I8 % In плавится лишь при 47 °С. Сплавы висмута эвтектического состава применяются в автоматических огнетушителях и в качестве припоев.
Мышьяк и сурьма используются главным образом в качестве добавки к свинцу для придания ему повышенной твердости. Важное значение имеет типографский сплав, содержащий 25 % Sb, 60% Рb и 15% Sn.
Соединения со степенью окисления мышьяка, сурьмы и висмута—3. В качестве солеподобных соединений, в которых мышьяк, сурьма и висмут проявляют степень окисления —3, можно рассматривать арсениды, стибиды (антимониды) и висмутиды s-элементов I и II групп (К3Э, Са3Э2, Мg3Э2 и др.). В большинстве же других случаев при взаимодействии металлов с мышьяком, сурьмой и висмутом образуются соединения металлического типа. Стибиды и арсениды р-элементов и элементов подгруппы цинка — полупроводники. В ряду однотипных нитридов, фосфидов, арсенидов, стибидов и висмутидов ширина запрещенной зоны уменьшается, что свидетельствует об увеличении доли нелокализованной связи. Например:
АlN АlР АlAs АlSb
DЕ, эВ ……………3,8 3,0 2,16 1,6
Большинство арсенидов, стибидов и висмутидов довольно легко разлагается кислотами.
Ослабление признаков неметаллических элементов в ряду Аs—Sb—Вi проявляется также в их соединениях с водородом Н3Э. Строение молекул Н3Э аналогично строению Н3N и H3Р. Но по мере увеличения размеров электронных облаков в ряду N—Р—As—Sb—Вi полярность и прочность связи Э — Н уменьшается. По этой же причине несвязывающее двухэлектронное облако становится пространственно менее направленным, значение валентного угла — ÐНЭН приближается к 90о и наблюдается уменьшение электрического момента диполя молекул. В обычных условиях Н3Аs (арсин), Н3Sb (стибин) и ВiН3 (висмутин) — газообразные вещества с резким запахом. Арсин, стибин и особенно висмутин сильно эндотермичны. При нагревании они довольно легко распадаются с образованием на стенках сосуда черного осадка с металлическим блеском (простые вещества Аs, Sb, Вi). В ряду Н3Аs—Н3Sb—ВiН3 устойчивость падает, вследствие чего висмутин недостаточно изучен. Все они сильные восстановители.
Образуются Н3Э действием разбавленных кислот на арсениды, стибиды и висмутиды:
Мg3Э2 6НСl = 3МgСl2 2Н3Э
а также действием цинка на подкисленные растворы соединений:
Аs2O3 6Zn I2НСl = 2Н3Аs 6ZnСl2 3Н2O
Арсин (в меньшей степени стибин и висмутин) очень токсичен. Поскольку цинк почти всегда содержит небольшие количества мышьяка, опасно вдыхать водород, выделяющийся при действии кислот на цинк.
В ряду Н3N—Н3Р—Н3Аs—Н3Sb—ВiН3 электронодонорные свойства молекул ослабевают. Так, если производные аммония вполне устойчивы, то арсоний-ион АsН5 обнаружен лишь с помощью ИК-спектра (в смеси Н3Аs и НI при низкой температуре). Ионы SbH4 и ВiН4 вообще не обнаружены.
В молекулах арсина и стибина связь почти неполярна и в зависимости от условий характер поляризации атомов Аs и Sb может изменяться. Поэтому для Н3Аs и Н3Sb характерен ряд свойств гидридов, т. е. производных Аs (III) и Sb (III). В частности, при взаимодействии арсина с растворами щелочей выделяется водород.
Соединении мышьяка (III), сурьмы (III) и висмута (III). В степени окисления 3 атомы Аs, Sb и Вi сохраняют несвязывающую электронную пару; имеют координационные числа 3, 4, 5 и 6. Этим координационным числам отвечают структурные единицы в виде тригональной пирамиды искаженного тетраэдра, тетрагональной пирамиды, искаженного октаэдра соответственно.
Степень окисления 3 у мышьяка и его аналогов проявляется в галогенидах ЭНаl3, оксидах Э2О3, сульфидах Э2S3. Бинарные соединения и гидроксиды Э(III) амфотерны.
В ряду однотипных соединений Аs (III) — Sb (III) — Вi (III) кислотные признаки ослабевают и нарастают основные.
Оксиды Э2О3 получают прямым взаимодействием простых веществ, Sb2О3 также окислением сурьмы разбавленной НNО3, а Вi2О3 — термическим разложением Вi(NO3)3.
Структура оксидов в при переходе от Аs (III) к Вi (III) существенно изменяется. Кристаллы низкотемпературных модификаций Аs2О3 и Sb2O3 имеют, как и Р2O3, молекулярную решетку, построенную из молекул Э4O6. Последние состоят из четырех объединенных друг с другом пирамид ЭO3. В высокотемпературной модификации Sb2O3 пирамиды SbO3 связаны в бесконечные сдвоенные цепи:

Оксид висмута (III) Вi2O3 имеет координационную решетку с искаженной октаэдро-тетраэдрической координацией атомов. Различие в структуре, естественно, сказывается на свойствах оксидов.
Аs2O3 (белый мышьяк) — преимущественно кислотный оксид. Он растворяется в воде и щелочах, но в отличие от Р2О3 взаимодействует также с галогеноводородными кислотами:
Аs2O3 Н2О = 2Н3АsO3
Аs2O3 8НCl = 2HAsCl4 H2O
Sb2O3 в воде практически не растворяется, но взаимодействует со щелочами, а также с соляной кислотой.
Взаимодействие Аs2O3 с растворами щелочей приводит к образованию соответственно гидроксоарсенатов (III) (гидроксоарсенитов) и гидроксостибатов (III) (гидроксоантимонитов):
Э2О3 2КОН 3Н2О = 2К[Э(ОН)4]
Наоборот, Вi2О3 легко взаимодействует с кислотами, образуя разнообразные соли Вi (III), в воде не растворяется, со щелочами практически не реагирует.
Аналогично изменяются свойства и в ряду гидроксидов. В отличие от Н3РО3 гидроксиды Аs(ОН)3 и Sb(ОН)3 амфотерны: у первого преобладают кислотные свойства, у второго — основные. При этом и кислотная, и основная ионизации Э(ОН)3 в растворе выражены слабо.
В свободном состоянии Аs(ОН)3 не выделен, в водном растворе ведет себя как слабая кислота Н3АsО3, называемая мышьяковистой.
Гидроксиды Sb (III) и Вi (III) в воде практически не растворяются. Они получаются в виде белых осадков переменного состава Э2O3×nН2О при действии щелочей на катионные производные Э (III):
Bi(NO3)3 3KOH = Bi(OH)3¯ 3KNO3
или кислот на анионные производные Э (III):
Nа[Sb(ОН)4] НСl = NаСI Sb(ОН)3¯ Н2О
При сплавлении Э2O3 или Э(ОН)3 со щелочами обычно образуются полимерные метаарсенаты (III) (метаарсениты) и метастибаты (III) (метаантимониты) состава М 1ЭО2.
Оксовисмутаты (III) неустойчивы.
Ослабление кислотных признаков проявляется также в ряду сульфидов Э2S3. Желтый Аs2S3, оранжевый Sb2S3 и черно-бурый Вi2S3 твердые вещества, нерастворимые в воде.
Сульфиды образуются непосредственным взаимодействием простых веществ или действием сероводорода на растворимые соединения Э (III) в кислой среде:

Сульфиды Аs (III) и Sb (III) — преимущественно кислотные соединения. Они легко растворяются в присутствии основных сульфидов с образованием сульфидоарсенатов (III) и сульфидостибатов (III) типа М 1ЭS2 и М 13ЭS3:
Э2S3 (NH4)2S = 2NH4ЭS2
Растворяются As2S3 и Sb2S3 и в щелочах.
Сульфид висмута (III) Вi2S3 кислотные свойства в растворах не проявляет, с основными сульфидами взаимодействует лишь при сплавлении.
Соединения Э2S3 характеризуются сравнительно небольшими значениями энергий Гиббса образования; довольно легко переходят в Э2О3, ЭF3 и ЭСl3 при окислении кислородом, фтором и хлором, например:
2Sb2S3 9O2 = 2Sb2O3 6SO2
В отличие от Аs2S3 сульфиды Sb (III) и Вi (III) растворяются в концентрированной соляной кислоте:
Sb2S3 8НСI « 2НSbСl4 3Н2S
Тригалогениды элементов подгруппы мышьяка ЭНаl3 получают взаимодействием простых веществ при недостатке галогена. У большинства тригалидов элементов подгруппы мышьяка кристаллические решетки молекулярны. Температура плавления трифторида висмута, имеющего координационную решетку, наиболее высокая (730 °С).
Подобно Э2О3 и Э2S3, галогениды Аs (III) — кислотные соединения, галогениды Sb (III) и Вi (III) проявляют также свойства солей.
При гидролизе АsНаl3 образуются кислоты. Однако в отличие от РНаl3 гидролиз АsНаl3 обратим:
АsСl3 4Н2O = Н[Аs(ОН)4] 3НСl
Гидролитическое разложение галогенидов Sb (III) и Вi (III) также преобладает над их электролитической диссоциацией. Гидролиз протекает энергично до оксогалогенидов, например:
SbСl3 Н2O « SbОСl 2НСl
Оксогалогениды Sb (III) и Вi (III) состава ЭОНаl в обычных условиях – твердые, нерастворимые в воде вещества с координационнослоистой решеткой, структурно совершенно отличные от аналогичных соединений фосфора (III) и мышьяка (III).
Ослабление неметаллических свойств в ряду Аs – Sb – Вi проявляется также в изменении устойчивости солей и солеподобных соединений Э (III). Последние для Аs (III) неустойчивы и в свободном состоянии не выделены, а для Sb (III) известны сульфат Sb2(SO4)3, нитрат Sb(NО3)3 и некоторые другие. В воде эти соединения энергично разлагаются. Относительно устойчивы комплексные стибаты (III) s-элементов I группы, например сульфатостибаты (III) М 1[Sb(SO4)2].
Соли Вi (I1I) весьма разнообразны и устойчивы. Кислотные признаки у них проявляются в характере гидролиза (который у них преобладает над электролитической диссоциацией)
Вi(NО3)3 Н2O « ВiОNО3 2НNO3
и в способности образовывать производные типа M 1[Вi(SО4)2], М 1[Вi(NО3)4].
Соединения Аs (IП) довольно легко окисляются. Так, Аs2S3 окисляется персульфидом аммония:
Аs2S3 2(NН4)2S2 = 2NН4ЭS2
а Аs2О3 – азотной кислотой:
Аs2O3 4HNO3 7H2O = 6H3AsO4 4NO
У производных Sb (III) восстановительная активность проявляется в меньшей степени, однако Sb2S3 также окисляется персульфидом аммония. Окисление же соединений Вi (ПI) возможно лишь наиболее сильными окислителями в сильнощелочной среде, например:
ВiСl3 Сl2 6КОН = КВiО3 5КСl 3Н2O
Соединения мышьяка (V), сурьмы (V) и висмута (V). В ряду Аs (V) – Sb (V) – Вi (V) устойчивость соединений в целом падает. При рассмотрении подгрупп брома и селена было показано, что высшая степень окисления в этих подгруппах наиболее характерна для р-элементов 5-го периода, т. е. для I и Те. Наименее устойчива высшая степень окисления для р-элементов 6-го периода, т. е. для Аt и Ро. Подобная закономерность, хотя и выраженная — менее отчетливо, проявляется и в подгруппе мышьяка; степень окисления 5 наиболее характерна для Sb, менее характерна для Аs и неустойчива у Вi.
Для висмута (V) получен лишь фторид ВiF5, для мышьяка (V) и сурьмы (V), кроме того, известны оксиды Э2О5, сульфиды Э2S5, а для сурьмы (V) — еще и хлорид SbСl5:
По химической природе бинарные соединения мышьяка (V) и его аналогов кислотные. Им соответствуют анионные комплексы, простейшие из которых ЭНаl6—, ЭО43-, Э(ОН)6—.
Оксиды Э2O5 в обычных условиях твердые вещества. По структуре и свойствам Аs2O5 напоминает Р2O5, довольно хорошо растворяется в воде:
Аs2O5 3Н2O = 2Н3АsО4
Sb2O5 (желтого цвета) в воде растворим мало, лучше в щелочных растворах:
Sb2O5 2КОН 5Н2О = 2К[Sb (ОН)6]
Оксоарсенаты (V) и оксостибаты (V), образующиеся при сплавлении Аs2O5 и Sb2О5 со щелочами и оксидами металлов, в большинстве полимерны.
Структура оксоарсенатов обычно подобна структуре оксофосфатов (V).
Чаще всего полимерные висмутаты отвечают составу М 1ВiО3.
Из растворов обычно выделяются тетраоксоарсенаты типа М 13АsО4 и гексагидроксостибаты типа М 1[Sb(ОН)6]. Подобно фосфатам арсенаты, стибаты и висмутаты, как правило, трудно растворимы в воде.
Из соответствующих соединений водорода в свободном состоянии получен лишь оксоарсенат (V) водорода Н3АsО4 (мышьяковая кислота) — твердое, растворимое в воде вещество, Н3АsО4 получают окислением Аs или Аs2О3 азотной кислотой. Мышьяковая кислота (К1 = 6×10-3) слабее фосфорной. При попытке получения сурьмяных кислот образуется осадок неопределенного состава Sb2O5×nН2О. Не выделены в свободном состоянии и висмутовые кислоты.
Сульфиды Э2S5 во многом напоминают оксиды Э2O3. Желтый Аs2S5 и оранжевый Sb2S5 с водой не взаимодействуют; будучи кислотными соединениями, они растворяются в присутствии основных сульфидов и при действии щелочей:
Э2S5 3Nа2S = 2Nа3ЭS4
Сульфиды Э2S5 можно получить либо взаимодействием простых веществ, либо осаждением при действии Н2S на производные Э(V) в кислой среде:
2Nа3АsО4 (р) 5Н2S (р) 6НСl (р) = Аs2S5 (т) 6NаС1 (р) 8Н2O (ж)
Соответствующие сульфидоарсенаты (V) и сульфидостибаты (V) (тиоанатимонаты) водорода в свободном состоянии неустойчивы.
Молекулы пентагалогенидов ЭНаl5, как и РНаl5, имеют форму тригональной бипирамиды.
В обычных условиях АsF5 — газ (Тпл. —80 °С, Ткип. —53 °С), а SbF5 (Тпл. 8 °С, Ткип. 142 °С) и SbСl (Тпл. 30 oС, Ткип. 140 оС) – жидкости; ВiF5 — твердое вещество (Тпл. 151 oС, Ткип. 230 °С). Резкое повышение точек плавления и кипения при переходе от АsF5 и SbF5 обусловливается ассоциацией молекул SbF5 в полимерные цепи, образованные октаэдрическими структурными единицами SbF6 (—SbF4 — F — SbF4 — F —). Пентагалиды типичные кислотные соединения. При взаимодействии с водой ЭНаl5 дают кислоты, с основными галогенидами образуют галогеноарсенаты (V) и галогеностибаты (V):
КF ЭF5 = К[ЭF6]
Пентафториды ЭF5—очень сильные акцепторы фторид-иона; при взаимодействии с ЭF5 основные свойства проявляют даже такие соединения, как НF, O2F2, N2F4, СlF5.
Производные типа М[ЭOF4] образованы полимерными анионами в виде цепи октаэдрических структурных единиц:
Соединения висмута (V) сильные окислители. Они, например, переводят Мn (II) в Мn (VII):
2Мn2 5ВiО3— 14Н = 5Вi3 2МnО4— 7Н2O
Производные сурьмы (V) окислительные свойства проявляют в меньшей степени, однако Sb2O5 может окислять концентрированную соляную кислоту по обратимой реакции:
Sb2O5 I0НСl « 2SbСl3 2Сl2 5Н2O
Применение соединений мышьяка, сурьмы и висмута весьма разнообразно. Так, производные Аs в сельском хозяйстве служат одним из основных средств борьбы с вредителями культурных растений. Например, Nа3АsО4, Са3(АsО4)2, Са(AsO2)2, и другие применяются как инсектициды. Важное применение соединения мышьяка (Аs2O3, КАsО2, органические производные) находят в медицине. Лекарства на их основе рекомендуют при малокровии, истощении, используют в стоматологической практике. Производные Аs, Sb и Bi нашли применение также в производстве керамики и в других областях.
Соединения сурьмы, висмута и в особенности мышьяка ядовиты.

