Молекулярная диффузия газов в жидкости. 2. коэффициенты молекулярной диффузии кислорода в воде
УДК 532
Молекулярная диффузия газов в жидкости. 2. Коэффициенты молекулярной диффузии кислорода в воде
Д-р техн. наук А.Г. Новоселов, dekrosh@mail.ru Е.Г. Селиверстова, С.А. Сорокин
Университет ИТМО 191002, Россия, Санкт-Петербург, ул. Ломоносова, 9
Канд. техн. наук А.Б. Дужий, Aleksey.Duzhiy@uralkali.com
ВНИИ Галургии
190103, Россия, Санкт-Петербург, ул. 10-я Красноармейская, 22, литера А
Выполнен анализ опубликованных в научно-технической литературе экспериментальных данных по коэффициентам молекулярной диффузии кислорода в воду, полученных при атмосферном давлении и различных температурах. Предложена эмпирическая зависимость для расчета коэффициента молекулярной диффузии в диапазоне изменения температур 10^55°С. Полученная экспоненциальная зависимость коэффициента молекулярной диффузии от температуры хорошо согласуется с кинетической теорией механизма этого процесса. Высказано предположение, что коэффициент пропорциональности К в уравнении ВАВ = К ■ ехрь’1 зависит от величины мольного объема диффундирующего газа. Обработка экспериментальных данных, полученных различными метод ами, позволила определить численные значения коэффициентов К и Ь д ля системы кислород-вода.
Ключевые слова: молекулярная диффузия; кислород; вода; температурная зависимость. БОТ: 10.17586/2310-1164-2020-10-3-21-26
Diffusion of gases in liquids. 2. The molecular diffusion coefficients of oxygen in water
D. Sc. Alexander G. Novoselov, dekrosh@mail.ru Ekaterina G. Seliverstova, Sergei A. Sorokin
ITMO University 9, Lomonosov str., St. Petersburg, 191002, Russia
Ph. D. Alexey B. Duzhij, Aleksey.Duzhiy@uralkali.com
All-Russian Research Institute Galurgii A build., 22,10th Krasnoarmeyskaya str., St. Petersburg, 190103, Russia
The analysis of published in scientific and technical literature experimental data on the coefficients of molecular diffusion of oxygen into water, obtained at atmospheric pressure and different temperatures, is carried out. An empirical dependence is proposed for calculating the molecular diffusion coefficient in the temperature range of io^55°C. The obtained exponential temperature dependence of the molecular diffusion coefficient is in good agreement with the kinetic theory of the mechanism of this process. It has been suggested that the proportionality coefficient Kin the equation DAB = K • expb’ t depends on the molar volume of the diffusing gas. The processing of experimental data obtained by various methods made it possible to determine the numerical values of the coefficients K and b for the oxygen-water system. Keywords: molecular diffusion; oxygen; water; temperature dependence.
Введение
С физико-химическими свойствами газов и жидкостей приходится сталкиваться как научным работникам в области разработки фундаментальных основ процессов массопереноса, так и инженерам, занимающимся разработкой процессов и аппаратов пищевых, химических и биохимических технологий.
В общем случае процессы массопереноса разделяют на четыре характерные области, представляющие собой особый интерес и важность. Это молекулярная диффузия молекул газа в неподвижной жидкости; молекулярная диффузия молекул газа в движущейся в ламинарном режиме жидкости; турбулентная диффузия молекул газа в движущейся в турбулентном режиме жидкости и перенос молекул газа через межфазную границу.
Под молекулярной диффузией понимается перемещение молекул в результате их теплового движения. Миграция молекул в материальной системе, состоящей из молекул одного вещества, в условиях равенства химических потенциалов, называется самодиффузией. В этом случае не существует понятия направленного диффузионного потока, т.е. движения молекул в каком-либо направлении. С точки зрения понимания механизма массопереноса знание коэффициентов самодиффузии вещества не играет определяющей роли в определении скорости массообменного процесса, но становится важным фактором в понимании механизма молекулярной диффузии одного или нескольких веществ в другом.
Рассмотрение молекулярной диффузии с точки зрения направленного переноса целевого вещества предполагает наличие движущей силы. Обычно направленное движение перемещения молекул диффундирующего вещества возникает при наличии в данной материальной системе термодинамического неравновесия между пространственными областями этой системы, что обусловлено разностью химических потенциалов в этих областях. В свою очередь величина химического потенциала определяется концентрацией взаимодействующих молекул и силовыми полями вокруг каждой молекулы. При проведении процесса массопереноса молекулярный поток, в целевом направлении, может возникнуть и под влиянием других факторов. Основными из них являются температура и давление. Диффузия, возникающая под действием наличия градиента температуры, называется термодиффузией, а под действием давления — бародиффузией. В данной работе мы будем рассматривать процесс диффузии, обусловленный разностью концентраций растворенного диффундирующего газа А в воде В.
Процессы диффузии обычно рассматривают как на основе феноменологической, так и кинетической теорий. Феноменологические теории описывают наблюдаемые явления на основе соотношений между макроскопически измеряемыми величинами. Полученные, на основе экспериментальных данных, результаты вполне удовлетворяют требования инженеров-проектировщиков в рамках стоящих перед ними задач, но не позволяют детально изучить механизм самого процесса массопереноса.
Молекулярные теории диффузии основаны на попытках объяснить механизм процессов массопереноса и получить законы, управляющие этими процессами на основе молекулярной структуры данных газовой и жидкостной сред и их свойств. Как правило, такой подход базируется на кинетической и статистической теориях вещества. Основной задачей молекулярной теории процессов массопереноса является объяснение результатов экспериментов, полученных в феноменологических теориях молекулярной диффузии, а также возможность расчета коэффициентов молекулярной диффузии на основе величин массы и объема взаимодействующих молекул.
Как и в предыдущей статье [1], в основе сравнения коэффициентов молекулярной диффузии полученных экспериментальным путем с известными полуэмпирическими уравнениями, представленными в литературе различными исследователями, лежат шесть зависимостей. Это уравнения Уилки-Чанга [2], Шейбеля [3], Отмера-Тейкера [4], Сововы [5], Ибрахима и Кулора [6] и Акгермана-Гейнера [7]. Основная задача данной статьи — проанализировать известные значения коэффициентов молекулярной диффузии чистого кислорода в воде при различных температурах, предложить достаточно простое уравнение для расчета этого коэффициента и сравнить полученные значения с вышеупомянутыми зависимостями. Решение этой задачи позволяет более обоснованно подойти к расчетам коэффициентов молекулярной диффузии СО2 и О2 в питательных средах для проведения массообменных расчетов аппаратов, предназначенных для воспроизводства биомассы в дрожжевой и пивоваренной отраслях промышленности. Основу этих сред составляет вода с растворенными в ней питательными веществами. Для дрожжевого производства в качестве питательной среды используются водные растворы мелассы с добавлением питательных солей (диаммонийфосфат, сульфат аммония, хлористый калий, сернокислый магний). Для пивоваренного производства, в качестве питательной среды, используется пивное сусло, получаемое в результате водно-тепловой и ферментативной обработки измельченного ячменя. Наличие в воде даже в минимальных количествах солей и сахаров неизбежно приводит к изменению величины коэффициента молекулярной диффузии. Очевидно, что чем больше молекул «посторонних» веществ в воде, тем сильнее сказывается их присутствие в растворах на изменение скорости диффузии по отношению к скорости диффузии в «чистой» воде. Изучение этого влияния является целью дальнейших наших исследований. Коэффициенты молекулярной диффузии присутствуют во всех известных уравнениях массопереноса газов в жидкостных средах как теоретических, так
и эмпирических, и чем точнее они будут определены, тем надежнее будут результаты расчетов массообменного оборудования, предназначенного для аэробного культивирования биомассы.
Анализ выбранных экспериментальных значений коэффициента молекулярной
диффузии кислорода в воде
Результаты экспериментальных исследований по определению коэффициентов молекулярной диффузии газов в жидкости, в том числе и кислорода в воду, были опубликованы в ряде работ [8-18]. Определенную ценность, с точки зрения приближения к истинным значениям коэффициентов молекулярной диффузии Dab при различных температурах представляет тот факт, что собранные данные были получены различными методами и на различных экспериментальных установках, реализующих эти методы. В частности, в работах [8, 14] был применен метод уменьшающегося пузырька, так называемый DBS — метод, в работах [10, 16] — метод абсорбции газа через поверхность струи кольцевой формы, в работе [11] — метод орошаемой сферы, в работах [9, 13, 15, 18] — метод абсорбции газа через поверхность сплошной цилиндрической струи, а также метод лазерной интерферометрии [11] и метод Тэйлоровской диффузии в ламинарном потоке [17]. Подробное описание этих методов можно найти в оригинальных работах, а также в справочнике [19]. Следует отметить, что каждый из приведенных выше методов относится к косвенным методам измерений и имеет определенные преимущества и недостатки. В зависимости от выбранного метода и используемой измерительной техники, измерение физических величин неизбежно сопровождается погрешностями, которые обусловлены несовершенством методов и, собственно, самой измерительной техники, а также недостаточным учетом влияния условий внешней среды, субъективными ошибками исследователей.
Тем не менее, выбранный нами подход к оценке истинного значения Dab на основе экспериментальных данных, полученных различными исследователями, использовавших принципиально разные подходы и методы измерений, представляется вполне логичным. Недостатки одних методов исключены в других. Системы измерений также отличаются друг от друга. Происходит своеобразное нивелирование погрешностей измерений, имеющихся в одних методиках измерений, другими.
Результаты аналитической работы
Результаты проведенного аналитического анализа представлены на рисунке 1 в виде графической зависимости DAB = f(T). Аналитическая интерпретация линии тренда лучше всего описывается экспоненциальным уравнением вида
Dab = К• expb’f
и в окончательном варианте после определения численных значений коэффициентов К и b
г, 1 11/1 щ-9 0,0241-/ , л
Dab = 1,214 -10 — exp , (1)
в котором значение температуры t принимается в °C, а получаемое значение Dab в м2/с. Уравнение (1) хорошо согласуется с кинетической теорией механизма молекулярной диффузии, которая предполагает экспоненциальную зависимость Dab от температуры, т.е.
Г Ed }
Dab = K exp
RT J
где K — коэффициент, учитывающий размер диффундирующего вещества;
EDab — энергия активации молекул диффундирующего вещества, калл/моль;
R — газовая постоянная.
Рисунок 1 — Зависимость коэффициента молекулярной диффузии (система кислород-вода)
от температуры при атмосферном давлении Figure 1. The dependence of molecular diffusion coefficient (oxygen-water system) on the temperature under
atmospheric pressure
Сравнение рассчитанных по уравнению (1) значений коэффициентов молекулярной диффузии О2 в воде -Орасч с экспериментальными Dэксп приведено в таблице 1. Здесь же в процентах представлены значения относительного отклонения экспериментальных точек от полученной линии тренда. Максимальное отклонение экспериментальных значений Dэксп от расчетных значений составляет примерно 15% при среднеарифметическом отклонении 6,24%. Графическая интерпретация этих расхождений представлена на рисунке 2.
Таблица 1. Сравнение расчетных значений коэффициентов молекулярной диффузии Dрасч с экспериментальными Dэксп
Table 1. The empirical (Орасч) and experimental (Оэксп) values of molecular diffusion coefficient
t, °С экспериментальное D, м2/с расчетное D, м2/с относительная погрешность
10 1,54-10″9 1,54484-10-9 0,31%
15 1,51-10″9 1,74267-10-9 13,35%
15 1,67-10″9 1,74267-10-9 4,17%
15 1,78-10-9 1,74267-10-9 -2,14%
20 1,76-10″9 1,96584-10-9 10,47%
20 2,00-10-9 1,96584-10-9 -1,74%
20 2,01-10-9 1,96584-10-9 -2,25%
20 2,22-10-9 1,96584-10-9 -12,93%
23,8 2,30-10-9 2,15438-10-9 -6,76%
25 2,03-10-9 2,21759-10-9 8,46%
25 2,07-10-9 2,21759-10-9 6,66%
25 2,08-10-9 2,21759-10-9 6,20%
25 2,09-10-9 2,21759-10-9 5,75%
25 2,20-10-9 2,21759-10-9 0,79%
25 2,42-10-9 2,21759-10-9 -9,13%
25 2,55-10-9 2,21759-10-9 -14,99%
40 3,33-10-9 3,18331-10-9 -4,61%
55 4,50-10-9 4,56958-10-9 1,52%
Аналогичное сравнение значений Dab, рассчитанных по уравнению (1) со значениями, рассчитанными по известным из литературы [1-7] уравнениям, представлено в таблице 2. Более подробное описание этих уравнений, а также численные значения, входящих в них параметров для воды, как растворителя, можно найти в работе [19]. Вместе с тем авторы указывают, что в работе [1] была допущена ошибка технического характера. Таким образом, мольный объем воды, как растворителя, необходимо считать равным 18,7 см3/моль, а не 75,6 см3/моль [19, стр. 790].
5,0-10-9
4.0-10″9
о
СЧ
з.о-ю-9
-Г 2.0-10-9
1.0-10-9
/ ‘/ /
/.И
/ у •
1.0-10-9
2,0-10-9
3,0-10-9
4.0-109 5,0-10-9
D
расч-
м»/с
Рисунок 2 — Сравнение расчетных значений коэффициентов молекулярной диффузии Dpac4
экспериментальными Da^n Figure 2. The empirical (Орасч) and experimental (D^m) values of molecular diffusion coefficient
Таблица 2. Значения Dab кислорода в воде при температурах 10; 20 и 30°С, рассчитанные по уравнениям представленными в литературе
Table 2. The values of oxygen Dab in water at temperatures of 10; 20, and 30°С, calculated according to the equations presented in scientific publications
Уравнение Уилка-Чанга [2]; м2/с Уравнение Шейбеля [3]; м2/с Уравнение Отмера-Тейкера [4], м2/с Уравнение Сововы [5]; м2/с Уравнение Ибрахима и Кулоора [6], м2/с Уравнение Акгермана [7]; м2/с Уравнение (1) м2/с
1,5665^0-9 1,6188-10-9 1,4903-10-9 1,5545^10-9 2,1298-10-9 2,5899^10-9 1,5448^10-9
2,1155-10-9 2,1862-10-9 1,99б3-10-9 2,1102^10-9 2,1835-10-9 3,1546^10-9 1,9658-10-9
2,7469-10^9 2,8388-10-9 2,5644-10-9 2,7417^10-9 2,2481-10-9 3,7199^109 2,5016-10-9
Сравнивая уравнение (1) с уравнением, полученным нами для системы СО2-вода [1], видна очевидная тождественность этих уравнений. Можно предположить, что различие в величинах коэффициентов пропорциональности связано с молекулярной массой диффундирующего газа Ма и молекулярным объемом VA. Для СО2 и О2 эти величины составляют 44 и 32 г/моль, и 34 и 25,6 см3/моль соответственно. Так как молекулярный состав растворителя (воды) в обоих случаях одинаков, то различие в значениях Dab, скорее всего, будет определяться этими параметрами диффундирующих молекул. Этот факт отмечается и в работе [3], авторы которой, основываясь на кинетической теории механизма диффузии, предположили, что величина Dab определяется размером молекул диффундирующего газа, в первую очередь, его мольным объемом VA. Оценка этого влияния является одной из наших задач в изучении процесса молекулярной диффузии газов в жидкости.
Выводы
1. На основании проанализированных известных экспериментальных исследований по определению коэффициентов молекулярной диффузии кислорода в воду получено уравнение для прогнозирования изменения этого коэффициента от температуры в виде экспоненциальной зависимости.
2. Выполнено сравнение полученного уравнения с наиболее известными зависимостями, представленными ранее.
3. Полученное уравнение (1) будет положено в основу при обработке экспериментальных данных по молекулярной диффузии кислорода в водные растворы питательных сред дрожжевых и пивоваренных производств.
References
1. Novoselov A.G., Duzhij A.B., Golikova E.Y. Diffusion of Gases in Liquids. 1. The molecular diffusion coefficients of carbon dioxide in water. Processes and Food Production Equipment. 2022, no. 2 (In Russian).
2. Wilke C.R., Chang P. Correlation of diffusion coefficient in dilute solution. A. I. Ch. E.-J. 1955, V. 1, pp. 264-266.
3. Schibel E.G. Liquid diffusivities. Ind. Eng. Chem. 1954, V. 46, no. 9, pp. 2007-2008.
4. Othmer D.F., Thakar M.S. Correlating diffusion coefficients in Liquids. Ind. End. Chem. 1953, V. 45, no. 3, pp. 589-593.
5. Sovova H., Prochazka J. New method of measurement of diffusivities of gases in liquids. Chem. Eng. Sci. 1976, V. 31, Is.11, pp. 1091-1097.
6. Ibrahim S.H., Kuloor N.R. Diffusion in dilute solutions — a new correlation. Brit. Chem. Eng. 1960, V. 5, no. 11,
pp. 795-797.
7. Akgerman A., Gainer J.L. Diffusion of gases in liquids. Ind. Eng. Chem. Fundament. 1972, V. 11, pp. 373-379.
8. Wise D.L., Houghton G. The diffusion coefficients of ten slightly soluble gases in water at 10-60°C. Chem. Eng. Sci. 1966, V. 21, pp. 999-1010.
9. Ferrell R.T., Himmelblau D.M. Diffusion coefficients of nitrogen and oxygen in water. J. Chem. Eng. Data. 1967, V. 12, no. 1, pp. 111-115.
10. Baird M.H., Davidson J.F. Annular jets-2. Gas absorption. Chem. Eng. Sci. 1962, V. 17, pp. 473-478.
11. Davidson J.F., Cullen E.J. The determination of diffusion coefficients for sparingly soluble gases in liquids. Trans. Inst. Chem. Eng. 1957, V. 35, pp. 51-60.
12. O’Brien R.N., Hyslop W.F. A laser interferometric study of the diffusion of O2, N2, Н2 and Ar into water. Can. J. Chem. Eng. 1977, V. 55, pp. 1415-1422.
13. Witherspoon PA., Saraf D.N. Diffusion of methane, ethane, propane and n-butane in water from 25° to 43°C. J. Phys. Chem. 1965, V. 69, Is. 11, pp. 3752-3755.
14. Houghton G., Ritchie P.D., Thomson J.A. The rate of solution of small stationary bubbles and the diffusion coefficients of gases in liquids. Chem. Eng. Sci. 1962, V. 17, pp. 221-227.
15. Hershcovich E., Merchuk J.C., Tamir A. Diffusivity of oxygen in hemoglobin solutions and red blood cell suspensions. Chem. Eng. Sci. 1982, V. 37, no. 2, pp. 637-641.
16. Baird M.H., Davidson J.E. Annular jets-1. Fluid dynamics. Chem. Eng. Sci. 1962, V. 17, pp. 467-472.
17. Collingham R.E., Blackshear P.L., Eckert E.R. A versatible method for measuring diffusion coefficients and thermal conductivities in fluids. Chem. Eng. Prog., Symp. Ser. 1970, V. 66, Is. 102, pp. 141-149.
18. Vivian J.E., King C.J. Diffusivities of slightly soluble gases in water. A. J. Ch. E.-J. 1964, V. 10, no. 3, pp. 220-221.
19. Novoselov A.G., Tishin V.B., Duzhiy A.B. A handbook on molecular diffusion in gas-liquid and liquid-liquid systems. In A new reference book of a chemist and technologist. Processes and apparatus of chemical technology. Part II. St. Petersburg, Professional Publ., 2006. 916 p. (In Russian).
Статья поступила в редакцию 14.08.2020
Определение коэффициента взаимной диффузии воздуха и водяного пара
Диффузией называется явление проникновения двух или нескольких соприкасающихся веществ друг в друга. Диффузия сопровождается переносом массы диффундирующего вещества.
Рассмотрим явление диффузии в газах. Перенос массы связан с тепловым движением молекул. Скорости теплового движения молекул велики (они составляют сотни метров в секунду при комнатной температуре), и, казалось бы, диффузия должна происходить быстро. Однако, как показывает опыт, диффузия в газах довольно медленный процесс и может происходить сутками.
Причина этого несоответствия заключается в том, что, благодаря малой длине свободного пробега, молекулы непрерывно сталкиваются друг с другом. Поэтому молекула за одну секунду уходит на очень небольшое расстояние от того места, где она находилась. Для того, чтобы попасть из одной точки в другую, молекулы проходят длинный зигзагообразный путь, во много раз превосходящий расстояние по прямой между этими точками. Таким образом, молекулы газа не столько движутся вперед, сколько «толкутся» на одном месте. Следовательно, в газах механизмом, обеспечивающим явление диффузии, является столкновение молекул.
Опыт показывает, что при диффузии через некоторую площадку  переносится тем большая масса газа
переносится тем большая масса газа 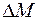 , чем больше размеры площадки
, чем больше размеры площадки  , чем за больший промежуток времени
, чем за больший промежуток времени 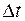 наблюдается диффузия и чем скорее меняется в направлении, перпендикулярном к площадке
наблюдается диффузия и чем скорее меняется в направлении, перпендикулярном к площадке  , плотность диффундирующего газа
, плотность диффундирующего газа 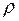 (рис. 1.1) :
(рис. 1.1) :
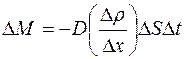 . (1.1)
. (1.1)
Величина 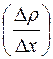 характеризует изменение плотности газа на единице длины в направлении оси
характеризует изменение плотности газа на единице длины в направлении оси 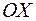 ; она называется градиентом плотности. Коэффициент
; она называется градиентом плотности. Коэффициент 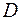 называется коэффициентом диффузии газа. Он зависит от сорта газа и условий, при которых газ находится.
называется коэффициентом диффузии газа. Он зависит от сорта газа и условий, при которых газ находится.
В газах различают самодиффузию, взаимную (концентрационную) диффузию и термодиффузию.
Самодиффузия − это диффузия молекул газа в среде того же газа. С явлением самодиффузии мы имеем дело, например, когда газовая смесь состоит из двух изотопов одного и того же вещества. Изотопы незначительно отличаются друг от друга массой, но не отличаются никакими другими свойствами. Явление самодиффузии можно наблюдать также в смеси газов, где часть молекул заменена другими по химическому составу молекулами, но имеющими почти такие же размеры и массу (например, 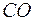 и
и 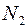 ).
).
Рассмотрим явление самодиффузии с точки зрения молекулярно-кинетической теории.

Рис. 1.1. Перенос молекул через площадку 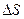 .
.
Так как молекулы одного и того же газа одинаковы, то для изучения процесса самодиффузии пометим часть молекул.
Допустим, что концентрации меченых молекул по обе стороны от площадки  (рис. 1.1) не одинаковы. Тогда меченые и немеченые молекулы, хаотически двигаясь, будут переходить через эту площадку в ту и другую сторону. Результирующий поток меченых молекул будет направлен оттуда, где их концентрация больше, туда, где она меньше. Тоже самое справедливо и для немеченых молекул, только их результирующий поток противоположен потоку меченых.
(рис. 1.1) не одинаковы. Тогда меченые и немеченые молекулы, хаотически двигаясь, будут переходить через эту площадку в ту и другую сторону. Результирующий поток меченых молекул будет направлен оттуда, где их концентрация больше, туда, где она меньше. Тоже самое справедливо и для немеченых молекул, только их результирующий поток противоположен потоку меченых.
Мысленно выделим справа и слева от площадки  на расстояниях от нее, равных средней длине свободного пробега
на расстояниях от нее, равных средней длине свободного пробега 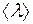 , одинаковые кубические объемы
, одинаковые кубические объемы 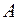 и
и 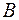 . Пусть боковые грани кубиков
. Пусть боковые грани кубиков 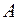 и
и 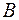 параллельны площадке
параллельны площадке  и равны ей по величине. Длину ребра кубиков обозначим через
и равны ей по величине. Длину ребра кубиков обозначим через 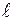 ;
; 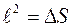 . Обозначим число меченых молекул в кубике
. Обозначим число меченых молекул в кубике 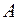 через
через 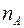 . Ввиду полной беспорядочности движения молекул газа, можно считать, что
. Ввиду полной беспорядочности движения молекул газа, можно считать, что 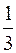 этих молекул движется вдоль оси
этих молекул движется вдоль оси 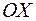 , из них
, из них 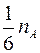 − в положительном направлении
− в положительном направлении 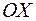 (т.е. к площадке
(т.е. к площадке  ), а
), а 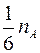 − в отрицательном направлении оси
− в отрицательном направлении оси 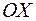 . Так как площадка
. Так как площадка  отстоит на расстоянии
отстоит на расстоянии 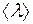 от кубика А, то все молекулы долетят до нее без столкновений и пролетят через
от кубика А, то все молекулы долетят до нее без столкновений и пролетят через  . Время
. Время 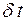 , за которое
, за которое 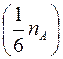 молекул пролетят через
молекул пролетят через  :
:
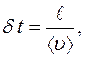
где 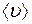 − средняя арифметическая скорость молекул.
− средняя арифметическая скорость молекул.
Таким образом, число меченых молекул 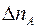 , пролетающих через площадку
, пролетающих через площадку  за единицу времени слева направо, равно:
за единицу времени слева направо, равно:

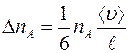 . (1.2)
. (1.2)
Обозначим через 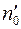 число меченых молекул в единице объема в том месте, где находится кубик
число меченых молекул в единице объема в том месте, где находится кубик 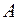 ; тогда
; тогда 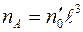 и
и
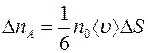 (1.3)
(1.3)
Точно также получим, что число меченых молекул 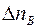 , пролетающих через площадку
, пролетающих через площадку  в единицу времени справа налево, будет равно:
в единицу времени справа налево, будет равно:
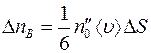 , (1.4)
, (1.4)
где 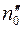 – число меченых молекул в единице объема в том месте, где находится кубик
– число меченых молекул в единице объема в том месте, где находится кубик 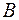 .
.
Отсюда разность между числом меченых молекул, пролетающих через  слева направо и справа налево за некоторый произвольный промежуток времени
слева направо и справа налево за некоторый произвольный промежуток времени 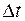 , равна:
, равна:
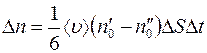 . (1.5)
. (1.5)
Массу 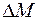 , переносимую через
, переносимую через  за время
за время 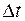 мечеными молекулами, получим, умножив число
мечеными молекулами, получим, умножив число 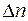 этих молекул на массу одной молекулы
этих молекул на массу одной молекулы 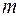 :
:
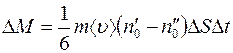 . (1.6)
. (1.6)
Разность 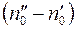 представляем в виде:
представляем в виде:
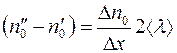 . (1.7)
. (1.7)
Тогда
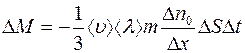 , (1.8)
, (1.8)
но 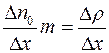 и, следовательно,
и, следовательно,

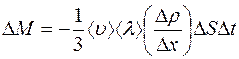 . (1.9)
. (1.9)
Сравнивая выражение (1.9) с формулой (1.1) получим:
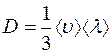 . (1.10)
. (1.10)
Таким образом, коэффициент диффузии 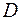 связан со средней длиной свободного пробега
связан со средней длиной свободного пробега 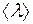 и средней скоростью
и средней скоростью 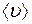 движения молекул.
движения молекул.
Средняя скорость движения молекул 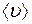 пропорциональна
пропорциональна 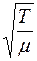 , где
, где 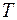 – абсолютная температура,
– абсолютная температура, 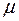 – молярная масса газа, а
– молярная масса газа, а 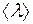 при постоянной плотности газа от его температуры не зависит. Отсюда следует, что для данного газа, при нагревании его при постоянном объеме, коэффициент диффузии
при постоянной плотности газа от его температуры не зависит. Отсюда следует, что для данного газа, при нагревании его при постоянном объеме, коэффициент диффузии 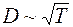 .
.
Средняя длина свободного пробега 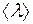 обратно пропорциональна давлению газа и
обратно пропорциональна давлению газа и 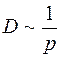 . Здесь
. Здесь 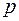 – суммарное давление смеси газов.
– суммарное давление смеси газов.
В разреженных газах диффузия происходит быстрее, чем в газах при больших давлениях.
Подставляя в (10) выражение для 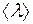 :
: 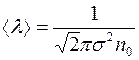 , получим:
, получим:
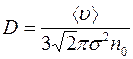 . (1.11)
. (1.11)
Следовательно, коэффициент диффузии оказывается непосредственно связанным с эффективным диаметром молекул 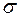 .
.
Величина коэффициента самодиффузии 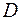 для того или иного газа при данной температуре и давлении не зависит ни от того, какую часть молекул мы пометили, ни от того, метили ли мы молекулы вообще. Этот коэффициент является характеристикой теплового движения молекул.
для того или иного газа при данной температуре и давлении не зависит ни от того, какую часть молекул мы пометили, ни от того, метили ли мы молекулы вообще. Этот коэффициент является характеристикой теплового движения молекул.
Отношение 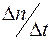 называется диффузионным потоком, а величина
называется диффузионным потоком, а величина 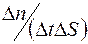 – удельным диффузионным потоком.
– удельным диффузионным потоком.
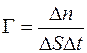 . (1.12)
. (1.12)
Согласно формулам (1.5) и (1.10),
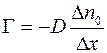 . (1.13)
. (1.13)
Соотношение (1.13) называется законом Фика.
Рассмотрим взаимную диффузию газов. Если в смеси двух различных газов 1 и 2, находящейся при постоянной температуре и постоянном давлении, компоненты смеси 1 и 2 распределены неравномерно, то начнется взаимная диффузия газов и в конце концов установится равномерное распределение молекул смеси по всему объему. Взаимная диффузия иначе называется концентрационной.
Если 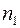 – число молекул газа 1, а
– число молекул газа 1, а 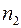 – число молекул газа 2 в единичном объеме смеси и если градиенты концентраций
– число молекул газа 2 в единичном объеме смеси и если градиенты концентраций 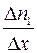 и
и 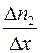 направлены вдоль оси
направлены вдоль оси 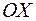 , то удельные диффузионные потоки
, то удельные диффузионные потоки 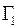 и
и 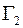 молекул газов 1 и 2 выразятся следующими равенствами:
молекул газов 1 и 2 выразятся следующими равенствами:
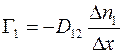 ;
;
(1.14)
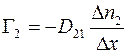 ,
,
где 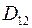 – коэффициент диффузии газа 1 в газ 2;
– коэффициент диффузии газа 1 в газ 2; 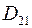 – коэффициент диффузии газа 2 в газ 1.
– коэффициент диффузии газа 2 в газ 1.
Если температура и давление в смеси всюду постоянны, то общее число молекул в единичном объеме также всюду постоянно, т.е. 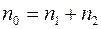 . Следовательно
. Следовательно
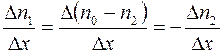 . (1.15)
. (1.15)
При этих условиях удельные диффузионные потоки молекул газа 1 и газа 2 также должны быть равными по величине, но противоположными по направлениям:
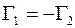 . (1.16)
. (1.16)
Из соотношений (1.14) – (1.16) следует, что
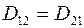 . (1.17)
. (1.17)
При взаимной диффузии газов существенно одинаковые или разные молекулы сталкиваются друг с другом, перед тем как пройти через сечение  , через которое осуществляется перенос массы газа. Диффузионный поток и коэффициент диффузии (1.17) обусловлены столкновениями разнородных молекул и не зависят от столкновений одинаковых молекул. Учет этого обстоятельства, основанный на понятии длины свободного пробега очень сложен. Приходится пользоваться двумя средними длинами свободного пробега (для газов 1 и 2), а между тем результаты плохо согласуются с экспериментом. Лучшие результаты дает теория, в которой понятие длины свободного пробега не используется. Эта теория для коэффициента диффузии дает следующее соотношение:
, через которое осуществляется перенос массы газа. Диффузионный поток и коэффициент диффузии (1.17) обусловлены столкновениями разнородных молекул и не зависят от столкновений одинаковых молекул. Учет этого обстоятельства, основанный на понятии длины свободного пробега очень сложен. Приходится пользоваться двумя средними длинами свободного пробега (для газов 1 и 2), а между тем результаты плохо согласуются с экспериментом. Лучшие результаты дает теория, в которой понятие длины свободного пробега не используется. Эта теория для коэффициента диффузии дает следующее соотношение:
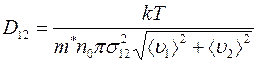 , (1.18)
, (1.18)
где 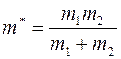 ;
; 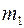 – масса молекулы 1-го газа,
– масса молекулы 1-го газа, 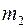 – масса молекулы 2-го газа;
– масса молекулы 2-го газа; 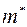 называется приведенной массой молекул газов 1 и 2.
называется приведенной массой молекул газов 1 и 2.
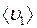 и
и 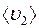 – средние скорости молекул газов 1 и 2 соответственно;
– средние скорости молекул газов 1 и 2 соответственно; 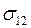 – эффективный диаметр столкновения разнородных молекул, который можно считать равным среднему диаметру молекул 1 и 2:
– эффективный диаметр столкновения разнородных молекул, который можно считать равным среднему диаметру молекул 1 и 2:
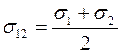
Отметим, что согласно выражению (1.18) коэффициент взаимной диффузии газов не зависит от концентраций компонент смеси 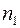 и
и 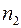 . Этот вывод подтверждается опытом.
. Этот вывод подтверждается опытом.
Диффузия может порождаться не только разницей концентраций компонент смеси двух газов, но и другими причинами. Одной из таких причин является неодинаковость температуры в разных частях объема смеси.
Заполним однородной смесью двух газов два сосуда, расположенных друг над другом и соединенных трубкой. Если верхний сосуд нагревать, а нижний охлаждать, то молекулы тяжелого газа обычно (но не всегда) диффундируют в направлении потока теплоты, а молекулы легкого газа – в обратном направлении. В результате произойдет частичное разделение компонент первоначально однородной смеси. Это явление называется тепловой (термической) диффузией.
Возникшее разделение компонент смеси приведет к взаимной диффузии, стремящейся устранить неоднородность концентраций различных газов смеси. Следовательно, эти два эффекта – термодиффузия и взаимная диффузия – действуют противоположным образом.
Если разность температур на концах сосудов, содержащих смесь газов, поддерживать постоянной, то установится стационарное состояние, при котором перенос молекул путем взаимной диффузии уравновешивается переносом их путем термодиффузии.
По своей природе термодиффузия отличается от самодиффузии и взаимной диффузии, которые обуславливались самим фактом столкновения молекул между собой. Термодиффузия обуславливается не самим фактом столкновения молекул, а зависимостью частоты столкновений между молекулами от их скорости. Коэффициент термодиффузии зависит от взаимодействия между разнородными молекулами. Если представить силы отталкивания между молекулами в виде 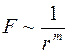 , где
, где 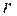 – расстояние между молекулами, то расчет показывает, что при
– расстояние между молекулами, то расчет показывает, что при 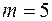 термодиффузия отсутствует. При
термодиффузия отсутствует. При 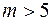 термодиффузия происходит так, что более горячие области обогащаются более легкой компонентой смеси, а при
термодиффузия происходит так, что более горячие области обогащаются более легкой компонентой смеси, а при 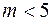 – более тяжелой. Следовательно, измеряя коэффициент термодиффузии, можно получить информацию о природе межмолекулярных сил.
– более тяжелой. Следовательно, измеряя коэффициент термодиффузии, можно получить информацию о природе межмолекулярных сил.
Термодиффузия получила важное применение для разделения изотопов. Ввиду близости масс изотопов обогащение состава смеси одним из изотопов при разумных градиентах температур невелико. Для значительного разделения изотопов используется многоступенчатый процесс, при котором на каждом последующем этапе обогащения в качестве исходной смеси берется смесь, обогащенная на предыдущем этапе.
Полная теория термодиффузии является очень сложной и обсуждается в специализированной литературе по диффузии.
§
Для определения коэффициента взаимной диффузии воздуха и водяного пара рассмотрим частично заполненную водой узкую трубку постоянного сечения S (капилляр), открытую с одного конца. Ось OX направим вдоль оси капилляра. На границе с водой (x=0) парциальное давление водяного пара pп в трубке равняется давлению насыщенного пара pн при температуре опыта. Давление водяного пара в капилляре меняется вдоль оси OX от значения pн до давления p1 около открытого конца капилляра. Давление p1 определяется влажностью воздуха в лаборатории. Таким образом, если предположить, что на расстоянии dx вдоль оси трубки давление водяного пара меняется на dpп, то градиент парциального давления пара равен 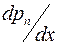 , и в трубке возникает диффузионный поток пара
, и в трубке возникает диффузионный поток пара 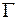 , направленный вверх.
, направленный вверх.
Масса пара, которая переносится через площадь поперечного сечения капилляра за одну секунду, согласно формулам (1.9) и (1.10), равна:
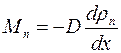 . (1.19).
. (1.19).
Плотность пара 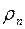 можно выразить через его парциальное давление, используя уравнение состояния идеального газа, следующим образом:
можно выразить через его парциальное давление, используя уравнение состояния идеального газа, следующим образом:
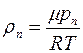 , (1.20)
, (1.20)
здесь 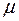 – молярная масса воды,
– молярная масса воды, 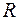 – универсальная газовая постоянная.
– универсальная газовая постоянная.
Подставляя (1.20) в формулу (1.19), получим6
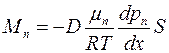 . (1.21)
. (1.21)
С другой стороны, массу пара 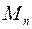 можно выразить через скорость понижения жидкости в капилляре:
можно выразить через скорость понижения жидкости в капилляре:
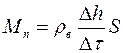 , (1.22)
, (1.22)
где 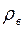 – плотность воды, а
– плотность воды, а 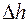 – понижение уровня жидкости в капилляре за время
– понижение уровня жидкости в капилляре за время 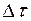 .
.
Подставляя соотношение (1.22) в уравнение (1.21), получим
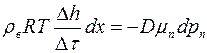 .
.
Интегрируя последнее равенство, получим:
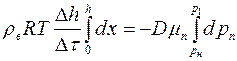
или

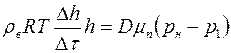 ,
,
откуда найдём коэффициент взаимной диффузии 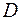 :
:
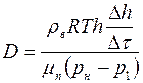 , (1.23)
, (1.23)
где 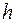 – расстояние от поверхности воды до верхнего края капилляра. Формулу (1.23) можно использовать для экспериментального определения коэффициента взаимной диффузии воздуха и водяного пара.
– расстояние от поверхности воды до верхнего края капилляра. Формулу (1.23) можно использовать для экспериментального определения коэффициента взаимной диффузии воздуха и водяного пара.
§
Для определения коэффициента взаимной диффузии воздуха и водяного пара предназначена экспериментальная установка (рис. 1.2).
В установке имеется микроскоп, на предметном столике которого размещен рабочий элемент, состоящий из измерителя, к подвижной части которого прикреплен корпус из оргстекла. Микроскоп снабжён двумя окулярами: один даёт увеличение в 25 ( 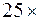 )
)  , второй– 50 (
, второй– 50 ( 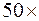 ) раз. В отверстии корпуса находятся стеклянная трубка (капилляр) с дистиллированной водой.
) раз. В отверстии корпуса находятся стеклянная трубка (капилляр) с дистиллированной водой.
Для подсветки трубки при измерениях применяется фонарь, свет от которого передается к рабочему элементу по световоду. Яркость свечения ламп устанавливается регулятором «Подсветка капилляра», который находится на передней панели блока приборов.
Рис. 1.2. Экспериментальная установка для определения коэффициента взаимной диффузии.
Время испарения воды в атмосферу через открытый конец капилляра измеряется секундомером, расположенным в блоке приборов и регистрируется на цифровом индикаторе «Время». Секундомер приводится в действие при включении блока приборов. Сброс на нуль значений на индикаторе производится нажатием кнопки «Останов», после отпускания которой снова начинается отсчет времени. Температура воздуха в блоке рабочего элемента измеряется полупроводниковым термометром и регистрируется на цифровом индикаторе «Температура» блока рабочего устройства. Цена деления 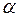 окулярной шкалы микроскопа указана на рабочем месте.
окулярной шкалы микроскопа указана на рабочем месте.
Измерения проводятся в следующей последовательности.
1. Снять защитный кожух с микроскопа и подвесить его на винтах на задней панели. Тубус микроскопа поставить в положение, при котором предметный столик с рабочим элементом располагается вертикально.
2. Убедившись в том, что регулятор подсветки капилляра находится в положении минимальной яркости, включить установку тумблером «Сеть».
3. Регулятором подсветки капилляра установить удобное для работы освещение и добиться четкого изображения капилляра. В поле зрения микроскопа наблюдается перевернутое изображение капилляра: вода, заполняющая капилляр будет сверху, а воздух над поверхностью воды– внизу. Граница раздела вода–воздух в капилляре представляет изогнутую поверхность или мениск.
4. Перемещая капилляр вращением гайки измерителя установить изображение мениска в нижней части окуляра микроскопа, учитывая, что при испарении жидкости перевёрнутое изображение мениска перемещается вверх. Записать положение мениска в делениях шкалы окуляра 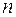 .
.
5. Включить отсчёт времени и, наблюдая в микроскоп за движением мениска жидкости, через каждые 3 деления шкалы окуляра занести в таблицу значения 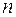 и время
и время 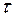 испарения жидкости.
испарения жидкости.
6. Установить изображение мениска в нижней части окуляра микроскопа, учитывая, что при испарении жидкости перевернутое изображение мениска перемещается вверх, записать положение мениска в делениях 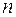 шкалы и включить отсчет времени.
шкалы и включить отсчет времени.
7. При выходе изображения мениска из поля зрения окуляра, вращением гайки измерителя вернуть изображение в начальное положение. Сделать 10-15 измерений положения мениска.
8. Измерить температуру воздуха в рабочем элементе установки.
9. Установить регулятор подсветки капилляра в положение минимальной яркости, после чего выключить установку тумблером «Сеть». Тубус микроскопа установить в вертикальное положение.
§
1. Построить график зависимости числа делений 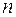 окулярной шкалы микроскопа от времени
окулярной шкалы микроскопа от времени 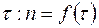 . Линеаризовав график с помощью метода наименьших квадратов, по наклону прямой определить значение
. Линеаризовав график с помощью метода наименьших квадратов, по наклону прямой определить значение 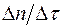 . Домножив эту величину на цену деления
. Домножив эту величину на цену деления 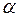 окулярной шкалы, найти среднее значение скорости испарения жидкости с капилляра
окулярной шкалы, найти среднее значение скорости испарения жидкости с капилляра 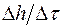 .
.
2. Используя найденное значение 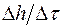 , по формуле (1.10) или (1.11) (по указанию преподавателя) вычислить коэффициент взаимной диффузии воздуха и водяного пара, учитывая, что плотность воды
, по формуле (1.10) или (1.11) (по указанию преподавателя) вычислить коэффициент взаимной диффузии воздуха и водяного пара, учитывая, что плотность воды 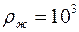 кг/м3, молярная масса воды
кг/м3, молярная масса воды 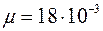 кг/моль. Давление насыщенного водяного пара определяется с помощью табл. 1, где приведена зависимость давления
кг/моль. Давление насыщенного водяного пара определяется с помощью табл. 1, где приведена зависимость давления 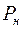 и плотность
и плотность 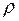 насыщенного водяного пара от температуры, а давление водяного пара
насыщенного водяного пара от температуры, а давление водяного пара 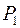 возле открытого конца трубки можно найти по значению относительной влажности
возле открытого конца трубки можно найти по значению относительной влажности 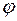 , %, в помещении лаборатории:
, %, в помещении лаборатории: 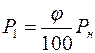 .
.
Таблица 1.
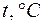 | 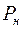 , кПа , кПа | 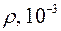 кг/м3 кг/м3 | 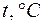 | 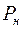 , кПа , кПа | 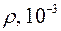 кг/м3 кг/м3 |
| 1,704 | 12,84 | 2,486 | 18,35 | ||
| 1,817 | 13,65 | 2,642 | 19,44 | ||
| 1,937 | 14,50 | 2,809 | 20,60 | ||
| 2,062 | 15,39 | 2,984 | 21,81 | ||
| 2,196 | 16,32 | 3,168 | 23,07 | ||
| 2,337 | 17,32 | 3,361 | 24,40 |
Коэффициент взаимной диффузии, определяемый в работе, рассчитывается по косвенным измерениям других физических величин. Поэтому для определения погрешности измерения 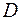 необходимо:
необходимо:
1. Рассчитать погрешности измерения уровней 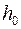 и
и 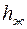 , которые складываются из случайной погрешности (опыт повторяется несколько раз) и приборной погрешности микроскопа по формулам (П.11) и (П.12) Приложения. В них
, которые складываются из случайной погрешности (опыт повторяется несколько раз) и приборной погрешности микроскопа по формулам (П.11) и (П.12) Приложения. В них 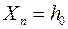 при определении положения верхнего края капилляра или
при определении положения верхнего края капилляра или 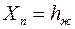 при определении положения мениска жидкости. Случайные погрешности для
при определении положения мениска жидкости. Случайные погрешности для 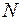 измерений находят по формуле (П.3). Значения коэффициентов Стьюдента
измерений находят по формуле (П.3). Значения коэффициентов Стьюдента 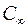 и
и 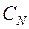 берутся из табл. П.1 Приложения. Приборная погрешность микроскопа равна
берутся из табл. П.1 Приложения. Приборная погрешность микроскопа равна 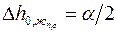 .
.
2. Определить погрешность измерения времени испарения воды из капилляра 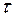 , которая складывается из случайной погрешности, рассчитываемой по формуле, аналогичной (П.3) и приборной погрешности электронного таймера, которая, согласно паспорту установки, составляет 5% измеренной величины.
, которая складывается из случайной погрешности, рассчитываемой по формуле, аналогичной (П.3) и приборной погрешности электронного таймера, которая, согласно паспорту установки, составляет 5% измеренной величины.
3. Рассчитать погрешность линеаризации скорости испарения жидкости 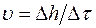 по формулам (П.6) и (П.7) приложения, в которых
по формулам (П.6) и (П.7) приложения, в которых 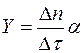 ,
, 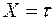 . Рассчитать погрешность определения коэффициента взаимной диффузии
. Рассчитать погрешность определения коэффициента взаимной диффузии 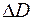 . Из (1.10) по методике расчета погрешности косвенного измерения получаем:
. Из (1.10) по методике расчета погрешности косвенного измерения получаем:
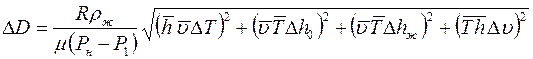
Приборная погрешность полупроводникового термометра 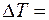 0,5.
0,5.
4. Результат представить в виде 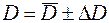 .
.
§
Известны три способа передачи теплоты: теплопроводность, конвекция и лучеиспускание. Только при конвекции и теплопроводности в передаче теплоты участвует газ. Конвекция обусловлена разностью плотностей нагретых и холодных слоев газа: в поле тяготения более нагретые слои поднимаются вверх, а более холодные опускаются вниз.
Если в соседних слоях газа создана и поддерживается разная температура, то между ними будет происходить обмен тепла. Средняя энергия молекул газа, пропорциональная абсолютной температуре 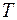 , в обоих слоях будет различной. Благодаря хаотическому движению, молекулы в обоих слоях будут перемешиваться, и средние энергии, а, следовательно, и температуры слоев будут выравниваться. При этом будет наблюдаться перенос энергии от более нагретых к более холодным слоям. Этот процесс носит название теплопроводности.
, в обоих слоях будет различной. Благодаря хаотическому движению, молекулы в обоих слоях будут перемешиваться, и средние энергии, а, следовательно, и температуры слоев будут выравниваться. При этом будет наблюдаться перенос энергии от более нагретых к более холодным слоям. Этот процесс носит название теплопроводности.
Опыт показывает, что количество теплоты, переносимое в газе через некоторую площадку  при теплопроводности будет тем больше, чем больше площадка
при теплопроводности будет тем больше, чем больше площадка  , чем больше промежуток времени
, чем больше промежуток времени 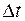 , за который наблюдается перенос тепла, и чем быстрее происходит изменение температуры
, за который наблюдается перенос тепла, и чем быстрее происходит изменение температуры 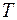 в направлении оси
в направлении оси 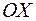 , перпендикулярной к площадке
, перпендикулярной к площадке  , т.е. чем выше градиент температуры
, т.е. чем выше градиент температуры 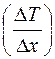 (рис. 2.1):
(рис. 2.1):
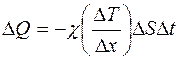 . (2.1)
. (2.1)
Коэффициент пропорциональности 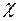 называется коэффициентом теплопроводности.
называется коэффициентом теплопроводности.
Отношение количества теплоты 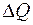 , проходящего через площадку
, проходящего через площадку  за время
за время 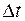 , ко времени
, ко времени 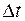 называется тепловым потоком:
называется тепловым потоком:
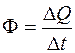 . (2.2)
. (2.2)
Отношение теплового потока 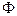 , проходящего через площадку
, проходящего через площадку  , к величине
, к величине  называется удельным тепловым потоком
называется удельным тепловым потоком 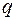 :
:
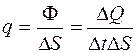 . (2.3)
. (2.3)
Из уравнений (2.1) – (2.3) получаем:
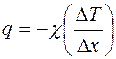 . (2.4)
. (2.4)
Знак минус означает, что тепло переносится в сторону убывания температуры.
Уравнение (2.4) называется законом Фурье для теплопроводности: удельный тепловой поток при теплопроводности прямо пропорционален градиенту температуры.
Из уравнения (2.4) следует физический смысл коэффициента теплопроводности: коэффициент теплопроводности численно равен удельному тепловому потоку при единичном градиенте температуры.
Уравнение (2.4) описывает стационарный процесс теплопроводности, при котором разность температур между горячим и холодным слоями со временем не изменяется и градиент температуры в каждой точке тоже не меняется со временем.
Рассмотрим стационарный процесс теплопроводности с точки зрения молекулярно-кинетической теории газов.
Согласно молекулярно – кинетической теории, перенос количества теплоты 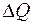 через площадку
через площадку  (рис. 2.1) означает перенос определенного количества кинетической энергии беспорядочно движущихся молекул.
(рис. 2.1) означает перенос определенного количества кинетической энергии беспорядочно движущихся молекул.
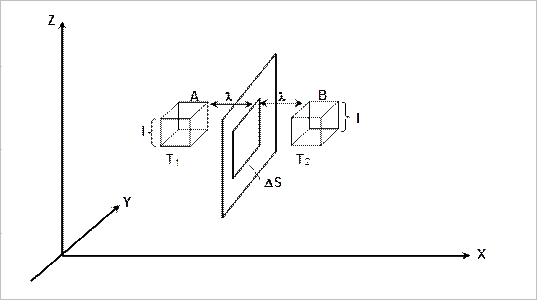
Рис. 2.1. Перенос молекулами энергии
Примем, что температура 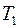 больше, чем
больше, чем 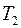 . Введем в рассмотрение два кубика
. Введем в рассмотрение два кубика 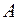 и
и 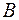 , расположенные слева и справа от площадки
, расположенные слева и справа от площадки  на расстояниях, равных средней длине свободного пробега
на расстояниях, равных средней длине свободного пробега 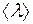 . Через площадку
. Через площадку  проходят молекулы как слева направо, так и справа налево. Если давление газа во всех точках одно и тоже, то число молекул
проходят молекулы как слева направо, так и справа налево. Если давление газа во всех точках одно и тоже, то число молекул 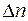 , пересекающих в единицу времени площадку
, пересекающих в единицу времени площадку  слева и справа, одинаково (см. лабораторную работу 1) и равно:
слева и справа, одинаково (см. лабораторную работу 1) и равно:
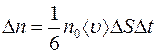 . (2.5)
. (2.5)
Все молекулы, подошедшие к  слева обладают средней кинетической энергией
слева обладают средней кинетической энергией
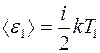 ,
,
где 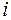 — число степеней свободы молекулы.
— число степеней свободы молекулы.
Эти молекулы переносят через площадку  количество энергии равное
количество энергии равное
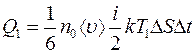 . (2.6)
. (2.6)
Аналогично этому: количество энергии, переносимое молекулами, подходящими к площадке  справа
справа
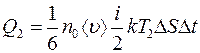 . (2.7)
. (2.7)
В результате через площадку  будет перенесено тепло:
будет перенесено тепло:
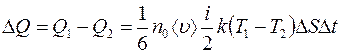 . (2.8)
. (2.8)
Разность температур 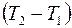 между точками, находящимися по обе стороны от площадки
между точками, находящимися по обе стороны от площадки  на расстоянии
на расстоянии 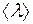 от нее, можно представить так:
от нее, можно представить так:
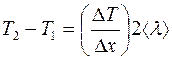 .
.
Отсюда:
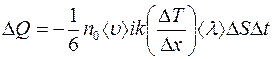 . (2.9)
. (2.9)
Сравнивая это значение 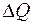 со значением (2.1), для коэффициента теплопроводности найдем:
со значением (2.1), для коэффициента теплопроводности найдем:
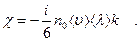 (2.10)
(2.10)
Величину 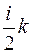 преобразуем следующим образом:
преобразуем следующим образом:
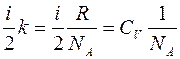 , (2.11)
, (2.11)
где 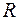 – универсальная газовая постоянная;
– универсальная газовая постоянная; 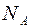 – число Авогадро; а
– число Авогадро; а 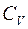 –молярная теплоемкость газа при постоянном объеме.
–молярная теплоемкость газа при постоянном объеме.
Тогда
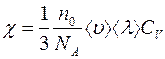 (2.12)
(2.12)
или
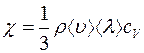 , (2.13)
, (2.13)
где 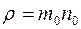 (
( 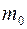 – масса одной молекулы газа) – плотность газа;
– масса одной молекулы газа) – плотность газа; 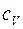 – удельная теплоемкость при постоянном объеме.
– удельная теплоемкость при постоянном объеме.
Из входящих в соотношение (2.13) величин число молекул в единице объема 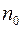 и средняя длина свободного пробега
и средняя длина свободного пробега 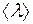 зависят от давления. Но первая из них пропорциональна, а вторая – обратно пропорциональна давлению газа. Следовательно, коэффициент теплопроводности
зависят от давления. Но первая из них пропорциональна, а вторая – обратно пропорциональна давлению газа. Следовательно, коэффициент теплопроводности 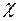 от давления не зависит. Этот вывод находится в полном согласии с опытными данными.
от давления не зависит. Этот вывод находится в полном согласии с опытными данными.
Из выражения (2.13) следует, что коэффициент теплопроводности, зависящий от средней скорости теплового движения молекул 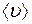 , должен меняться с изменением температуры как
, должен меняться с изменением температуры как 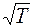 . В действительности, коэффициент теплопроводности растет несколько быстрее, чем
. В действительности, коэффициент теплопроводности растет несколько быстрее, чем 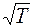 . Этот экспериментальный факт можно объяснить тем, что коэффициент теплопроводности пропорционален
. Этот экспериментальный факт можно объяснить тем, что коэффициент теплопроводности пропорционален 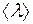 , которая тоже растет с температурой.
, которая тоже растет с температурой.
Возрастание 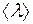 с температурой связано с тем, что молекулы газа нельзя рассматривать как твердые шарики. В самом деле, из молекулярно-кинетической теории следует, что средняя длина свободного пробега
с температурой связано с тем, что молекулы газа нельзя рассматривать как твердые шарики. В самом деле, из молекулярно-кинетической теории следует, что средняя длина свободного пробега 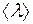 , равна:
, равна:
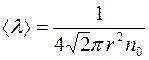 (2.14)
(2.14)
и не зависит от температуры ( 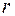 – эффективный радиус молекулы). Опыт показывает, что такая зависимость, хотя и слабая, существует: с повышением температуры длина свободного пробега растет. Это объясняется тем, что
– эффективный радиус молекулы). Опыт показывает, что такая зависимость, хотя и слабая, существует: с повышением температуры длина свободного пробега растет. Это объясняется тем, что 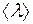 обратно пропорциональна поперечному сечению молекулы
обратно пропорциональна поперечному сечению молекулы 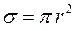 . Поперечное сечение молекулы
. Поперечное сечение молекулы 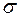 определяется тем расстоянием, на которое сближаются молекулы при столкновениях, т.е. расстоянием, на котором сила взаимодействия между молекулами вызывает уже заметное изменение направления их движения.
определяется тем расстоянием, на которое сближаются молекулы при столкновениях, т.е. расстоянием, на котором сила взаимодействия между молекулами вызывает уже заметное изменение направления их движения.
Поперечное сечение молекул должно, таким образом, зависеть от их скорости (энергии), так как при одной и той же силе взаимодействия быстрые молекулы испытывают меньшее отклонения от своего пути, чем более медленные молекулы. Поэтому, чем больше скорость молекул, тем меньше должно быть расстояние между ними при столкновении. Следовательно, с увеличением скорости молекул, т.е. с повышением температуры газа, поперечное сечение молекул уменьшается, а длина свободного пробега растет.
§
Экспериментальное изучение теплопроводности газов затрудняется тем, что перенос тепла в газе может происходить не только при теплопроводности, но и при конвекции, легко возникающей в газе. Конвекция, так же как и теплопроводность, стремится выровнять температуры в газе, поэтому отличить на опыте эти два механизма теплопередачи затруднительно, и при измерении теплопроводности необходимо обеспечить такие условия, при которых конвекция не может возникнуть.
Один из наиболее распространенных методов измерения коэффициента теплопроводности газов состоит в следующем.
Исследуемым газом заполняют пространство между двумя коаксиальными цилиндрами с радиусами 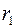 и
и 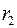 (рис. 2.2), один из которых (почти всегда – внутренний) нагревается электрической печью, потребляющей мощность
(рис. 2.2), один из которых (почти всегда – внутренний) нагревается электрической печью, потребляющей мощность 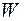 , а другой охлаждается так, чтобы его температура
, а другой охлаждается так, чтобы его температура 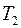 оставалась все время постоянной. Внутренним цилиндром, в частности, может быть тонкая металлическая нить, по которой пропускается электрический ток, так что она же служит и нагревателем.
оставалась все время постоянной. Внутренним цилиндром, в частности, может быть тонкая металлическая нить, по которой пропускается электрический ток, так что она же служит и нагревателем.
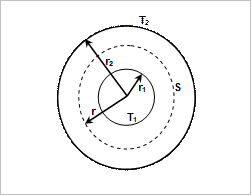
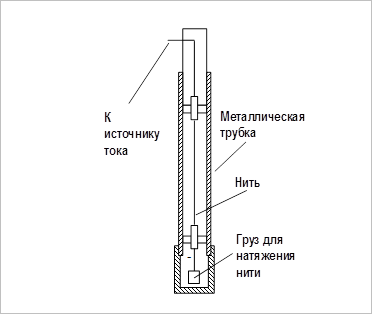
Рис. 2.2. Принципиальная схема установки
для определения коэффициента теплопроводности в газах
Через некоторое время после включения нагревателя устанавливается стационарное состояние, при котором температура 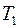 нити тоже становится постоянной.
нити тоже становится постоянной.
Тем самым между внешним цилиндром и нитью установится постоянная разность температур 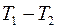 . Величина этой разности температур зависит от теплопроводности газа. Найдем эту зависимость.
. Величина этой разности температур зависит от теплопроводности газа. Найдем эту зависимость.
Если высота цилиндра равна 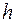 (во избежание ошибки, связанной с конвекцией, прибор следует устанавливать вертикально), тепловой поток
(во избежание ошибки, связанной с конвекцией, прибор следует устанавливать вертикально), тепловой поток 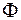 через любое цилиндрическое сечение
через любое цилиндрическое сечение 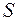 радиуса
радиуса 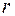 определяется уравнением:
определяется уравнением:
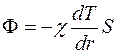 ,
,
где 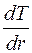 – градиент температуры4
– градиент температуры4 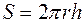 . Если высота цилиндра достаточно велика по сравнению с его радиусом, то температуру вдоль оси цилиндра можно считать всюду одинаковой.
. Если высота цилиндра достаточно велика по сравнению с его радиусом, то температуру вдоль оси цилиндра можно считать всюду одинаковой.
В стационарном состоянии 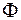 равно мощности нагревателя
равно мощности нагревателя 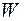 . Следовательно,
. Следовательно,
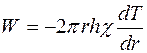 ,
,
откуда
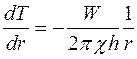 или
или
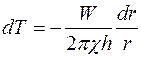 .
.
Интегрируя последнее уравнение, получаем:
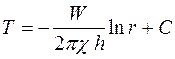 ,
,
где 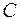 – постоянная интегрирования, которую можно исключить, принимая во внимание, что температура
– постоянная интегрирования, которую можно исключить, принимая во внимание, что температура 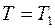 при
при 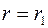 и
и 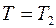 при
при 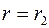 , т.е.
, т.е.
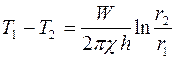 . (2.15)
. (2.15)
Измерив температуры 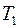 и
и 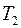 , зная геометрические размеры прибора и мощность нагревателя, можно вычислить коэффициент теплопроводности:
, зная геометрические размеры прибора и мощность нагревателя, можно вычислить коэффициент теплопроводности:
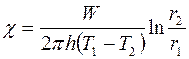 . (2.16)
. (2.16)
Мощность нагревателя 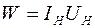 , где
, где 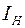 и
и 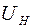 – сила тока и падение напряжения на нити.
– сила тока и падение напряжения на нити.
Температура трубки 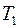 во время эксперимента остается постоянной и равной комнатной, т.к. ее поверхность обдувается с помощью вентилятора потоком воздуха.
во время эксперимента остается постоянной и равной комнатной, т.к. ее поверхность обдувается с помощью вентилятора потоком воздуха.
Для определения температуры нити 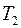 находят ее сопротивление в нагретом состоянии, используя известную зависимость сопротивления от температуры:
находят ее сопротивление в нагретом состоянии, используя известную зависимость сопротивления от температуры:
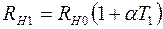 ; (2.17)
; (2.17)
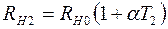 , (2.18)
, (2.18)
где 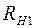 ,
, 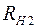 – сопротивления нити при температурах
– сопротивления нити при температурах 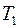 и
и 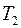 соответственно;
соответственно; 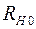 – сопротивление нити при
– сопротивление нити при 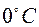 ;
; 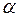 – температурный коэффициент сопротивления нити.
– температурный коэффициент сопротивления нити.
Из соотношений (2.17) и (2.18) выразим температуру 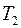 :
:
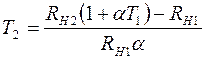 . (2.19)
. (2.19)
Следовательно, разность температур нити и стенок трубки 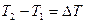 равна:
равна:
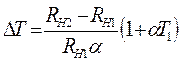 . (2.20)
. (2.20)
Для определения сопротивления нити при комнатной температуре и в нагретом состоянии, последовательно с ней включают эталонный резистор с сопротивлением 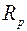 . Тогда токи, текущие по нити и через эталонный резистор оказываются одинаковыми:
. Тогда токи, текущие по нити и через эталонный резистор оказываются одинаковыми:
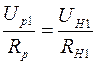 и
и 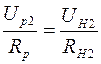 , (2.21)
, (2.21)
где 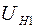 ,
, 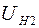 – падения напряжений на нити при температурах
– падения напряжений на нити при температурах 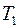 и
и 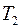 ;
; 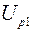 ,
, 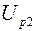 – соответствующие падения напряжений на эталонном резисторе.
– соответствующие падения напряжений на эталонном резисторе.
Используя соотношения (2.21) для разности температур, получаем
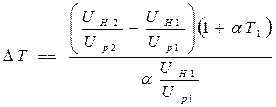 . (2.22)
. (2.22)
Мощность нагревателя 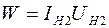 с учетом соотношения (2.21) можно представить в виде:
с учетом соотношения (2.21) можно представить в виде:
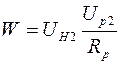 . (2.23)
. (2.23)
Подставляя (2.22) и (2.23) в выражение (2.16) для коэффициента теплопроводности, получим:
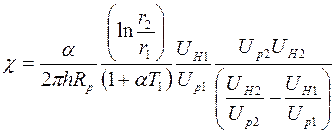 . (2.24)
. (2.24)
Соотношение (2.24) представляет собой рабочую формулу для вычисления коэффициента теплопроводности 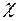 .
.
§
Для проведения измерений предназначена установка, представленная на рис. 2.3.
Температура воздуха в трубке определяется цифровым термометром. Значения падения напряжений на эталонном резисторе и на нити измеряются цифровым вольтметром.
Температура нити и, следовательно, значения напряжения на нити меняется с помощью регулятора «Нагрев».
Геометрические размеры рабочего элемента (радиус трубки, радиус нити, высота трубки), сопротивление эталонного резистора и температурный коэффициент нити указаны на стенде со справочными данными в лаборатории.
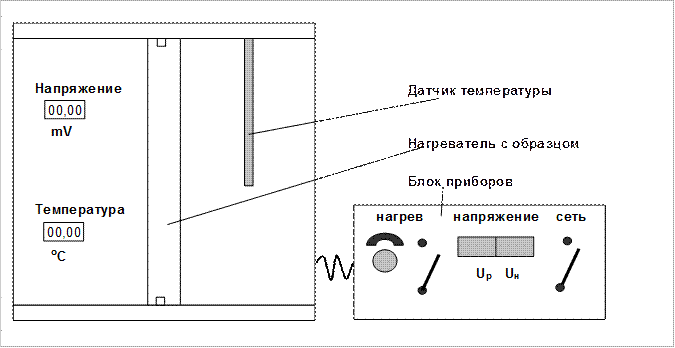 Рис. 2.3. Экспериментальная установка для определения
Рис. 2.3. Экспериментальная установка для определения
коэффициента теплопроводности воздуха.
Эксперимент осуществляется в следующей последовательности.
1. Включить установку тумблером «Сеть». Включить тумблер «Нагрев».
2. Нажать кнопку 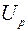 (режим измерения падения напряжения на эталонном резисторе) и установить регулятором «Нагрев» падение напряжения не более 0,06 В. При этом температура проволоки остается практически неизменной (ненагревающий ток). Измерить при помощи индикатора 2 напряжение на резисторе
(режим измерения падения напряжения на эталонном резисторе) и установить регулятором «Нагрев» падение напряжения не более 0,06 В. При этом температура проволоки остается практически неизменной (ненагревающий ток). Измерить при помощи индикатора 2 напряжение на резисторе 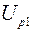 и записать его значение в таблицу.
и записать его значение в таблицу.
3. Нажать кнопку 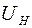 и записать показания индикатора 2
и записать показания индикатора 2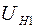 .
.
4. Повторить измерения п.п. 2,3 для нескольких значений напряжения 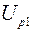 . Все результаты занести в таблицу.
. Все результаты занести в таблицу.
5. Нажать кнопку 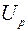 , и с помощью регулятора «Нагрев» установить падение напряжения на эталонном резисторе
, и с помощью регулятора «Нагрев» установить падение напряжения на эталонном резисторе 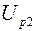 в диапазоне 0,3-1,5 мВ.
в диапазоне 0,3-1,5 мВ.
6. Подождав 2 минуты, что необходимо для стабилизации теплового режима рабочего элемента, нажать кнопку 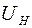 и определить падение напряжения на нити
и определить падение напряжения на нити 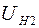 .
.
7. Повторить измерения п.п. 5 и 6 для нескольких значений падения напряжения 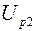 . Результаты измерений записать в таблицу.
. Результаты измерений записать в таблицу.
8. После измерений вывести ручку «Нагрев» на минимум; отключить тумблер «Нагрев»; выключить установку.
9. По формуле (2.24) рассчитать значения коэффициента теплопроводности 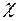 .
.
§
Основными величинами, которыми оперирует термодинамика, являются внутренняя энергия термодинамической системы U , теплота Q, переданная ей , и совершенная системой работа A.
Внутренняя энергия тела U представляет собой полную энергию беспорядочного движения молекул ( поступательного, колебательного и вращательного ).
При взаимодействии термодинамической системы с окружающими телами происходит обмен энергией. При этом возможны два различных способа передачи энергии от системы к внешним телам: с изменением внешних параметров системы и без изменения этих параметров. Первый способ передачи энергии называется работой, второй – теплотой.
Теплота, работа и внутренняя энергия связаны между собой соотношением:
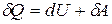 . (3.1)
. (3.1)
Соотношение (3.1) представляет собой I начало термодинамики: количество теплоты 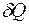 , переданное системе, идёт на увеличение её
, переданное системе, идёт на увеличение её
внутренней энергии 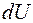 и на работу
и на работу 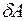 , совершаемую силами, приложенными со стороны системы к внешним телам.
, совершаемую силами, приложенными со стороны системы к внешним телам.
Из определения внутренней энергии следует, что в любом состоянии системы она имеет определённое значение, которое не зависит от того, каким способом это состояние было получено. Внутренняя энергия 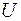 является функцией состояния термодинамической системы. Если система совершает круговой (циклический) процесс, то полное изменение её внутренней энергии
является функцией состояния термодинамической системы. Если система совершает круговой (циклический) процесс, то полное изменение её внутренней энергии 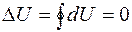 . Математически это означает, что подинтегральное выражение
. Математически это означает, что подинтегральное выражение 
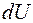 является полным дифференциалом некоторой функции.
является полным дифференциалом некоторой функции.
Работа 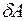 , совершаемая в круговом процессе, во всех случаях, когда имеет место нагревание, не равна нулю. Это означает, что работа A не является функцией состояния системы. Работа – это функция процесса. Следовательно, элементарная работа
, совершаемая в круговом процессе, во всех случаях, когда имеет место нагревание, не равна нулю. Это означает, что работа A не является функцией состояния системы. Работа – это функция процесса. Следовательно, элементарная работа 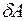 в (3.1) не представляет собой полного дифференциала. То же самое относится к количеству теплоты: в разных термодинамических процессах количество теплоты, которое требуется для нагревании системы от температуры T1 до температуры T2 различно. Количество теплоты не является функцией состоянии системы, а элементарная теплота
в (3.1) не представляет собой полного дифференциала. То же самое относится к количеству теплоты: в разных термодинамических процессах количество теплоты, которое требуется для нагревании системы от температуры T1 до температуры T2 различно. Количество теплоты не является функцией состоянии системы, а элементарная теплота 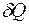 не является полным дифференциалом.
не является полным дифференциалом.
Опыт показывает, что две формы передачи энергии в форме теплоты и в форме работы не являются равноценными. При преобразовании работы в теплоту можно ограничиться только двумя телами, из которых одно передаёт при тепловом контакте энергию другому. При превращении теплоты в работу необходимо иметь по меньшей мере три тела: первое отдаёт энергию в форме теплоты (нагреватель), второе получает эту теплоту и отдаёт энергию в форме работы (рабочее тело) и третье тело, которому рабочее тело непременно отдаёт часть полученной от нагревателя теплоты (холодильник).
Такая неравноправность превращения теплоты в работу по сравнению с превращением работы в теплоту, связана с односторонностью естественных процессов.
Для рассмотрения этого свойства термодинамических процессов введём понятия квазистатического, обратимого и необратимого процессов.
Система находится в термодинамическом равновесии, если макроскопические величины, определяющие её состояние остаются постоянными и равными своим средним значениям. В случае идеального газа, например, такими макроскопическими величинами являются прежде всего давление и температура. В состоянии равновесия не могут происходить такие явления, как теплопроводность, диффузия, химические реакции, фазовые переходы.
Процессы, в ходе которых система всё время остаётся в состоянии равновесия, называются квазистатическими.
Если термодинамическая система по каким – либо причинам не находится в состоянии равновесия или выведена из него и после этого предоставлена самой себе, то, как показывает опыт, сам собой происходит переход к равновесному состоянию.
Процесс перехода к равновесию называется релаксацией, а время, требующееся на это, называется временем релаксации.
Реальный процесс можно считать квазистатическим, если скорость изменения какого – либо параметра системы (например, давления в газе) гораздо меньше средней скорости изменения этого параметра при релаксации.
Когда равновесие уже установилось, система не может сама собой возвратиться в первоначальное неравновесное состояние.
Так, например, если два соприкасающихся тела обладали в начале разностью температур и были предоставлены самим себе, то, в конце концов, температуры обоих тел выравниваются. Но обратный процесс – увеличение разности температур между ними – без внешнего воздействия не происходит.
Газ сам по себе всегда распределяется равномерно по всему объёму сосуда, и такое состояние соответствует равновесию. Но газ никогда не скапливается в одной части сосуда в большем количестве (с большей плотностью), чем в другой, без действия внешних сил.
Точно также, если ввести в сосуд два разных газа, то вследствие взаимной диффузии они сами собой перемешаются, так что состав смеси станет всюду одинаковым. Это и будет равновесным состоянием. Однако, чтобы разделить газы, требуется затратить большие усилия извне.
Приведённые примеры показывают, что естественные процессы идут в определённом направлении: от неравновесного состояния к равновесному. Эти процессы, происходящие в молекулярных системах, имеют важную особенность – они необратимы. Этим молекулярные процессы отличаются от чисто механических, для которых характерна строгая обратимость.
Обратимым процессом называется такое изменение состояния системы, которое, будучи проведено в обратном направлении, возвращает её в исходное состояние так, чтобы система прошла через те же промежуточные состояния, что и в прямом процессе, но в обратной последовательности, а состояние тел вне системы осталось неизменным.
Процессы, не удовлетворяющие этим условиям, являются необратимыми.
Все квазистатические процессы обратимы. Полностью необратимые процессы происходят часто. К числу таких процессов относятся расширение газа в пустоту, не уравновешенное внешними силами, теплопроводность, диффузия, внутреннее трение. Напротив, полностью необратимые процессы представляют собой идеальные предельные случаи реальных процессов. Все действительно происходящие процессы только частично обратимы; они всегда содержат необратимую часть.
Физическая величина, которая количественно характеризует направленность необратимых процессов и неравнозначность преобразования теплоты в работу и наоборот, называется энтропией.
Введём понятие энтропии на примере идеального газа. Разделим обе части равенства (3.1) на абсолютную температуру Т:
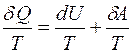 . (3.2)
. (3.2)
В случае идеального газа
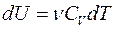 , (3.3)
, (3.3)
где 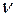 – количество газа;
– количество газа; 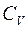 – молярная теплоёмкость газа при постоянном объёме,
– молярная теплоёмкость газа при постоянном объёме, 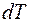 – изменение его температуры.
– изменение его температуры.
Элементарная работа
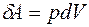 , (3.4)
, (3.4)
где р – давление; dV – изменение объёма газа.
Из уравнения Клапейрона- Менделеева:
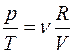 . (3.5)
. (3.5)
Подставляя (3.3)-(3.5) в уравнение (3.2), получим:
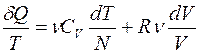 . (3.6)
. (3.6)
Учитывая, что 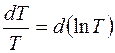 и
и 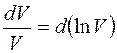 , перепишем уравнение (6) в виде
, перепишем уравнение (6) в виде
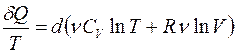 . (3.7)
. (3.7)
Правая часть этого равенства представляет собой полный дифференциал, следовательно, и левая часть 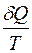 также есть полный
также есть полный
дифференциал некоторой функции S:
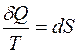 . (3.8)
. (3.8)
Введенная таким образом функция S называется энтропией. Энтропия, также как и внутренняя энергия, является функцией состояния системы, поэтому
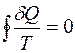 (равенство Клаузиуса). (3.9)
(равенство Клаузиуса). (3.9)
Заметим, что уравнение Клапейрона-Менделеева описывает квазистатические процессы, происходящие в идеальных газах, и, следовательно, выражения (3.8) и (3.9) получены лишь для обратимых процессов в идеальных газах.
В термодинамике доказывается, что соотношения (3.8) и (3.9) можно распространить на обратимые процессы и в системах, отличных от идеального газа. При любом обратимом изменении состояния замкнутой системы энтропия системы не изменяется. Из равенств (3.1) и (3.8) имеем:
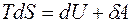 . (3.10)
. (3.10)
Уравнение (3.10) называется термодинамическим тождеством или вторым началом термодинамики для обратимых процессов.
Важной особенностью энтропии является её поведение в необратимых процессах. Если круговой процесс необратим, то можно показать, что
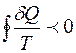 (неравенство Клаузиуса). (3.11)
(неравенство Клаузиуса). (3.11)
Рассмотрим процесс, при котором система необратимым образом переходит из равновесного состояния 1 в равновесное состояние 2. Необратимость перехода означает, что промежуточные состояния неравновесны. Вернём систему в исходное состояние каким – либо обратимым путем 2-1 (рис. 3.1). Получившийся круговой процесс необратим, потому что одна его часть необратима. Поэтому для него справедливо неравенство (3.11):
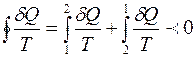 . (3.12)
. (3.12)
Второй интеграл относится к обратимому процессу и равен:
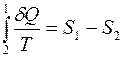 (3.13)
(3.13) 
Следовательно
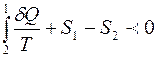
или
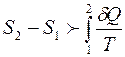 .
.
Если система замкнута, т.е изолирована от источников теплоты, то 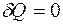 и
и 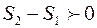 или
или
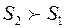 . (3.14)
. (3.14)
Отсюда следует, что энтропия замкнутой системы при необратимом процессе возрастает.
Обобщая выводы о поведении энтропии в замкнутых системах (3.9) и (3.14), можно утверждать, что энтропия замкнутой системы не убывает (второе начало термодинамики).
В необратимых процессах в замкнутых системах энтропия всегда возрастает, и это свойство также присуще энтропии, как энергии свойственно сохраняться при любых процессах в замкнутых системах.
Именно потому, что энергия обладает свойством сохраняться в замкнутой системе, она не может служить функцией, показывающей, в каком направлении идут процессы в такой системе. Энтропия в естественно идущих процессах всегда возрастающая, позволяет судить, какое направление процесса возможно и какое нет, какое состояние является начальным и какое конечным.
Рост энтропии в любом процессе продолжается не беспредельно, а лишь до определенного максимального значения, характерного для данной системы. Это максимальное значение энтропии соответствует состоянию равновесия, и после того как оно достигнуто, какие бы то ни было изменения состояния без внешнего воздействия прекращаются.
Энтропия как функция состояния существенно отличается от энергии. В то время как энергия не может быть ни создана, ни уничтожена, энтропия может создаваться и она постоянно создаётся во всяком процессе перехода к равновесию. Но, однажды созданная, она уже не может быть уничтожена: обратный процесс с уменьшением энтропии не может идти.
§
Рассчитаем изменение энтропии при плавлении и нагревании вещества. Плавлением называется процесс перехода из твердого состояния вещества в жидкое. Плавление происходит при определённой для каждого вещества температуре и сопровождается поглощением энергии в виде скрытой теплоты плавления. «Скрытой» она называется потому, что подвод этой теплоты не сопровождается повышением температуры. Количество теплоты, которое требуется для того, чтобы расплавить единичную массу вещества, называется удельной теплотой плавления 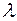 .
.
Обратный процесс перехода из жидкого состояния в твёрдое называется кристаллизацией. Процесс кристаллизации происходит при той же температуре, что и плавление и сопровождается выделением энергии в виде скрытой теплоты кристаллизации, равной по величине теплоте плавления.
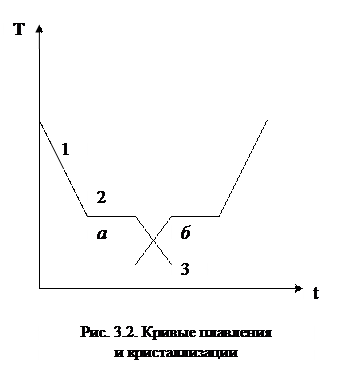 Это ясно видно из графика зависимости темпе-ратуры охлаждающейся (на-гревающейся) жидкости от времени (рис. 3.2). Участок 1 кривой а даёт ход мо-нотонного понижения темпе-ратуры жидкости вследствие отвода тепла от неё. Горизонтальный участок 2 показывает, что при опре-делённом значении темпера-туры её понижение прекра-щается, несмотря на то, что отвод тепла продолжается. Через некоторое время температура опять начинает понижаться (участок 3). Температура, соответствую-щая участку 2, и есть температура кристаллизации. Выделяющееся при кристаллизации тепло компенсирует отвод тепла от вещества, и поэтому понижение температуры временно прекращается. После окончания процесса кристаллизации температура теперь уже твёрдого тела вновь начинает понижаться.
Это ясно видно из графика зависимости темпе-ратуры охлаждающейся (на-гревающейся) жидкости от времени (рис. 3.2). Участок 1 кривой а даёт ход мо-нотонного понижения темпе-ратуры жидкости вследствие отвода тепла от неё. Горизонтальный участок 2 показывает, что при опре-делённом значении темпера-туры её понижение прекра-щается, несмотря на то, что отвод тепла продолжается. Через некоторое время температура опять начинает понижаться (участок 3). Температура, соответствую-щая участку 2, и есть температура кристаллизации. Выделяющееся при кристаллизации тепло компенсирует отвод тепла от вещества, и поэтому понижение температуры временно прекращается. После окончания процесса кристаллизации температура теперь уже твёрдого тела вновь начинает понижаться.
Такой ход графика понижения температуры характерен для кристаллических тел. При охлаждении аморфных веществ скрытая
теплота не выделяется, и график охлаждения представляет собой монотонную кривую без «остановки» охлаждения (участок 2).
При плавлении на кривой нагревания также наблюдается остановка в повышении температуры, вследствие поглощения скрытой теплоты плавления – теплоты, за счёт которойпроисходит разрушение кристаллической решетки (кривая б на рис. 3.2).
Процесс плавления будет квазистатическим, если плавление происходит в среде, температура которой на бесконечно малую величину превышает температуру плавления Тпл. Поэтому можно считать, чтонеобходимая для плавления теплота сообщается телу при постоянной температуре Тпл.В этом случае
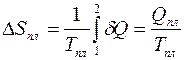 .
.
Поглощенная телом в процессе плавления теплота Q равна произведению удельной теплоты плавления 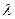 на массу расплавившегося тела m:
на массу расплавившегося тела m:
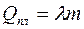 .
.
Таким образом, увеличение энтропии тела при квазистатическом плавлении равно:
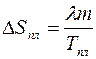 . (3.15)
. (3.15)
Если температура среды на бесконечно малую величину ниже температуры плавления, то возникает квазистатический процесс кристаллизации. При этом энтропия закристаллизовавшейся массы жидкости уменьшится настолько же, насколько увеличится энтропия при кристаллизации той же массы жидкости.
Изменение энтропии, отнесённое к единичной массе, называется её удельным приращением и определяется равенством
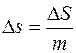 .
.
При плавлении удельное приращение энтропии равно: 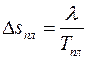 .
.
Рассмотрим процесс квазистатического нагревания вещества от температуры Т1 до температуры Т2. Если тело массы m поглощает тепло 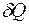 и при этом его температура повышается на
и при этом его температура повышается на 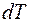 , то
, то
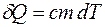 , (3.16)
, (3.16)
где с – удельная теплоёмкость вещества.
Подставив (3.16) в (3.8) находим, что
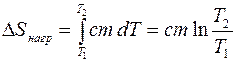 . (3.17)
. (3.17)
Приращение энтропии олова при его нагревании от комнатной температуры Т0 до температуры плавления Тпл и последующем плавлении:
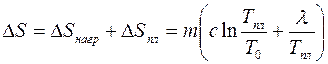 . (3.18)
. (3.18)
Для того, чтобы по формуле (18) рассчитать приращение энтропии олова необходимо знать его температуру плавления, которую в данной лабораторной работе предлагается определить экспериментально по кривой зависимости температуры Т от времени t в процессах нагревания, плавления и кристаллизации олова.
§
§
I начало термодинамики утверждает, что количество теплоты, переданное термодинамической системе, идёт на увеличение её внутренней энергии и на работу, совершаемую силами, приложенными со стороны системы к внешним телам:
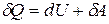 . (4.1)
. (4.1)
Элементарная работа, совершаемая газом при бесконечно малом изменении объёма 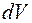 , когда давление газа
, когда давление газа 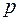 можно считать неизменным, равна
можно считать неизменным, равна
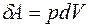 . (4.2)
. (4.2)
Для идеального газа элементарное изменение внутренней энергии 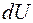 определятся изменением его температуры
определятся изменением его температуры 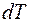 и равно:
и равно:
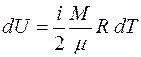 , (4.3)
, (4.3)
где 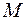 – масса газа;
– масса газа; 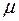 – его молярная масса;
– его молярная масса; 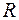 – универсальная газовая постоянная,
– универсальная газовая постоянная, 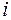 – число степеней свободы молекул газа.
– число степеней свободы молекул газа.
Числом степеней свободы 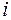 называют число независимых координат, определяющих положение молекулы в пространстве. Например, число степеней свободы для одноатомной молекулы, равно трём, для жесткой двухатомной – пяти.
называют число независимых координат, определяющих положение молекулы в пространстве. Например, число степеней свободы для одноатомной молекулы, равно трём, для жесткой двухатомной – пяти.
Количество теплоты 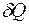 , требуемое для нагревания газа, зависит от количества нагреваемого газа и от того, на сколько градусов должна быть изменена его температура. Поэтому для характеристики тепловых свойств газа используется теплоёмкость.
, требуемое для нагревания газа, зависит от количества нагреваемого газа и от того, на сколько градусов должна быть изменена его температура. Поэтому для характеристики тепловых свойств газа используется теплоёмкость.
Удельной теплоёмкостью газа называется величина, равная количеств теплоты, которую необходимо сообщить единице массы газа для увеличения его температуры на 1 К:
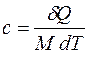 . (4.4)
. (4.4)
Теплоемкость одного моля вещества называется молярной теплоемкостью:
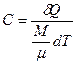 . (4.5)
. (4.5)
Значение теплоемкости газов зависит от условий их нагревания. Запишем I начало термодинамики и найдём теплоёмкости идеальных газов в различных термодинамических процессах.
В случае изохорного процесса 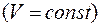 I начало термодинамики принимает вид:
I начало термодинамики принимает вид:
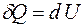 . (4.6)
. (4.6)
Учитывая (4.3) и (4.5), для молярной теплоёмкости при постоянном объёме получим:
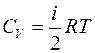 . (4.7)
. (4.7)
При изотермическом процессе ( 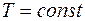 ),
), 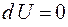 и I начало термодинамики запишется так:
и I начало термодинамики запишется так:
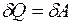 . (4.8)
. (4.8)
Теплоёмкость газа становится бесконечно большой 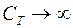 . Это относится к идеальному изотермическому процессу, который возможен лишь при идеально хорошем обмене теплом между газом и внешними телами. Практически приблизиться к изотермическому процессу можно, заставляя его протекать настолько медленно, чтобы температура газа все время успевала выравниваться с температурой окружающих тел.
. Это относится к идеальному изотермическому процессу, который возможен лишь при идеально хорошем обмене теплом между газом и внешними телами. Практически приблизиться к изотермическому процессу можно, заставляя его протекать настолько медленно, чтобы температура газа все время успевала выравниваться с температурой окружающих тел.
Если в газе протекает процесс изобарный ( 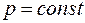 ), то I начало термодинамики имеет вид:
), то I начало термодинамики имеет вид:
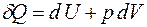 (4.9)
(4.9)
или
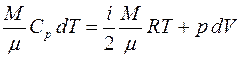 . (4.10)
. (4.10)
Из уравнения Менделеева- Клапейрона имеем
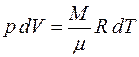 .
.
Тогда из уравнения (4.10) для молярной теплоёмкости газа при постоянном давлении, получаем
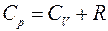 . (4.11)
. (4.11)
Таким образом, молярная теплоёмкость при постоянном давлении 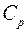 превосходит молярную теплоёмкость при постоянном объёме
превосходит молярную теплоёмкость при постоянном объёме 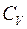 на универсальную газовую постоянную
на универсальную газовую постоянную 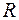 . Это объясняется тем, что при нагревании газа при постоянном давлении газ расширяется. Сообщаемое ему извне тепло идёт не только на увеличение запаса его внутренней энергии
. Это объясняется тем, что при нагревании газа при постоянном давлении газ расширяется. Сообщаемое ему извне тепло идёт не только на увеличение запаса его внутренней энергии 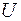 , но и на совершение работы
, но и на совершение работы 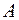 против внешних сил.
против внешних сил.
Процесс, протекающий в газе без теплообмена с окружающей средой ( 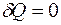 ), называется адиабатным. В этом случае I начало термодинамики имеет вид
), называется адиабатным. В этом случае I начало термодинамики имеет вид
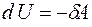
или
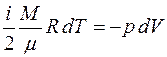 . (4.12)
. (4.12)
Из соотношения (4.12) следует, что при адиабатном сжатии газа ( 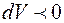 ), он нагревается (
), он нагревается ( 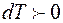 ); при адиабатном расширении (
); при адиабатном расширении ( 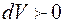 ) – газ охлаждается (
) – газ охлаждается ( 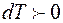 ).
).
Таким образом, при адиабатном изменении объёма газа его температура не остаётся постоянной, а молярная теплоёмкость газа
равна 0.
Cоответственный расчёт позволяет связать это изменение температуры 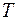 с изменением его объёма
с изменением его объёма 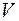 . Пусть газ, занимая объём
. Пусть газ, занимая объём 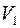 , имел температуру
, имел температуру 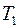 , тогда при адиабатном изменении объёма до значения
, тогда при адиабатном изменении объёма до значения 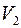 , температура примет значение
, температура примет значение 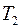 , причём будет иметь место следующее соотношение:
, причём будет иметь место следующее соотношение:
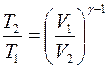 , (4.13)
, (4.13)
где 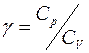 , т. е.
, т. е. 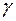 есть отношение теплоёмкостей газа при постоянном давлении и постоянном объёме. Величина
есть отношение теплоёмкостей газа при постоянном давлении и постоянном объёме. Величина 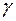 называется показателем адиабаты.
называется показателем адиабаты.
Воспользовавшись формулой Менделеева-Клапейрона, справедливой для каждого данного состояния газа, получим:
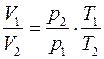 ;
;
подставив это значение 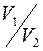 в (4.13), получим:
в (4.13), получим:
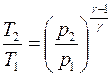 . (4.14)
. (4.14)
Формула (4.14), тождественная по своему смыслу с формулой (4.13), связывает изменение температуры, происходящее при адиабатном процессе, с изменением давления газа.
Приравнивая друг другу правые части выражений (4.13) и (4.14), получим
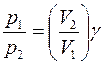 или
или 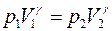 , (4.15)
, (4.15)
т.е. при адиабатном изменении объёма давление газа 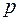 меняется обратно пропорционально объёму, взятому в степени
меняется обратно пропорционально объёму, взятому в степени 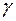 . Формула (4.15) носит название формулы Пуассона.
. Формула (4.15) носит название формулы Пуассона.
Практически процессы не носят строго адиабатного характера, так как невозможно осуществить полной термической изоляции газа. Но поскольку для совершения теплообмена необходимо некоторое время, то адиабатным можно считать процесс, который протекает настолько быстро, что система не успевает вступить в теплообмен с окружающей средой.
§
Метод определения показателя адиабаты, предложенный Клеманом и Дезормом, основывается на изучении параметров некоторой массы газа, переходящей из одного состояния в другое двумя последовательными процессами – адиабатным и изохорным. Эти процессы на диаграмме 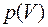 (рис. 3.1.) изображены кривыми соответственно 1-2 и 2-3.
(рис. 3.1.) изображены кривыми соответственно 1-2 и 2-3.
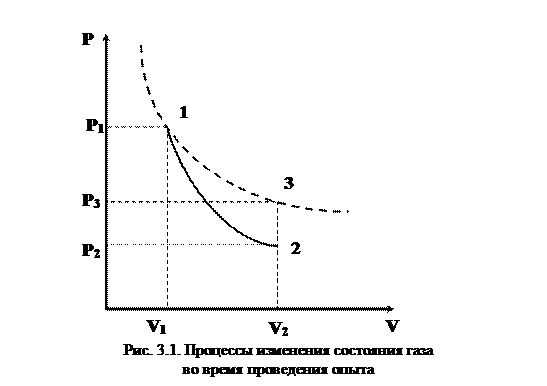
Если в баллон, соединенный с открытым водяным манометром, накачать воздух и подождать до установления теплового равновесия с окружающей средой, то в этом начальном состоянии 1 газ имеет параметры 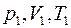 , причем температура газа в баллоне равна температуре окружающей среды
, причем температура газа в баллоне равна температуре окружающей среды 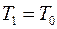 , а давление
, а давление 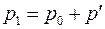 немного больше атмосферного.
немного больше атмосферного.
Если на короткое время соединить баллон с атмосферой, то произойдет адиабатное расширение воздуха. При этом воздух в баллоне перейдет в состояние 2, его давление понизится до атмосферного 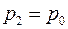 . Масса воздуха, оставшегося в баллоне, расширяясь, займет весь объем
. Масса воздуха, оставшегося в баллоне, расширяясь, займет весь объем 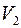 . При этом температура воздуха, оставшегося в баллоне, понизится до
. При этом температура воздуха, оставшегося в баллоне, понизится до 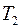 . Поскольку процесс 1-2 адиабатный, к нему можно применить уравнение Пуассона (4.15):
. Поскольку процесс 1-2 адиабатный, к нему можно применить уравнение Пуассона (4.15):
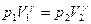 или
или 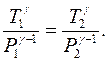
Отсюда
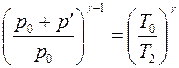 . (4.16)
. (4.16)
После кратковременного соединения баллона с атмосферой охлажденный из-за адиабатного расширения воздух в баллоне будет нагреваться (процесс 2-3) до температуры окружающей среды 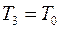 при постоянном объеме
при постоянном объеме 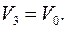 При этом давление в баллоне поднимется до
При этом давление в баллоне поднимется до 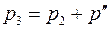 . Так как процесс 2-3 изохорный, то он удовлетворяет закон Шарля
. Так как процесс 2-3 изохорный, то он удовлетворяет закон Шарля 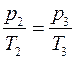 , отсюда
, отсюда
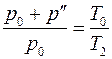 . (4.17)
. (4.17)
Из уравнений (4.16) и (4.17) получаем:
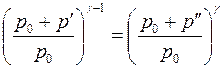 .
.
Прологарифмируем последнее соотношение:
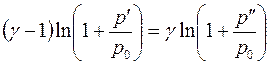 . (4.18)
. (4.18)
Избыточные давления 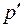 и
и 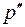 намного меньше атмосферного давления
намного меньше атмосферного давления 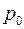 и, следовательно,
и, следовательно, 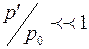 и
и 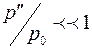 . Учитывая, что
. Учитывая, что 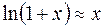 при
при 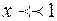 , перепишем выражение (4.18) следующим образом:
, перепишем выражение (4.18) следующим образом:
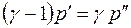 .
.
Отсюда для показателя адиабаты 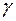 получаем:
получаем:
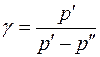 . (4.19)
. (4.19)
Избыточные давления 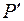 и
и 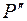 измеряют с помощью
измеряют с помощью 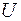 – образного манометра по разности уровней жидкости, обладающей плотностью
– образного манометра по разности уровней жидкости, обладающей плотностью 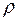 :
:
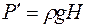 ,
, 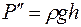 (4.20)
(4.20)
Из соотношений (4.19) и ( 4.20) получаем рабочую формулу для определения 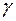 :
:
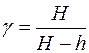 . (4.21)
. (4.21)
§
Для определения отношения теплоёмкостей воздуха 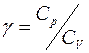 предназначена установка, схема которой представлена на рис. 4.2.
предназначена установка, схема которой представлена на рис. 4.2.
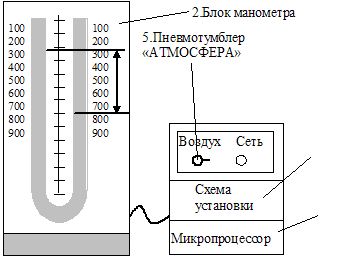 Установка состоит из стеклянной колбы, соединенной с открытым водяным манометром. Воздух нагнетается в колбу микропроцессором, размещенным в блоке рабочего элемента. Микропроцессор включается тумблером «Воздух», установ-ленным на передней панели блока приборов. Следует обратить внимание на своевременное отключение компрессора для предотвращения переливания воды из открытого колена
Установка состоит из стеклянной колбы, соединенной с открытым водяным манометром. Воздух нагнетается в колбу микропроцессором, размещенным в блоке рабочего элемента. Микропроцессор включается тумблером «Воздух», установ-ленным на передней панели блока приборов. Следует обратить внимание на своевременное отключение компрессора для предотвращения переливания воды из открытого колена 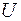 – образной трубки. Пневмотумблер «Атмосфера», расположенный на панели блока рабочего элемента, в положении «Открыто» позволяет соединить колбу с атмосферой.
– образной трубки. Пневмотумблер «Атмосфера», расположенный на панели блока рабочего элемента, в положении «Открыто» позволяет соединить колбу с атмосферой.
|
Измерения проводятся в следующей последовательности.
1. Включить установку тумблером «Сеть».
2. Установить пневмотумблер «Атмосфера» в положение «Закрыто». Для подачи воздуха в колбу включить тумблер «Воздух».
3. С помощью манометра контролируют давление в колбе. Когда разность уровней воды в манометре достигнет 150-200 мм вод. ст., отключить подачу воздуха.
4. Подождать 2–3 минуты, пока температура воздуха в колбе сравняется с температурой окружающей среды 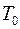 ; в колбе при этом установится постоянное давление
; в колбе при этом установится постоянное давление 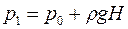 .
.
5. Определить разность уровней 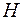 , установившуюся в коленах манометра. Полученное значение занести в таблицу.
, установившуюся в коленах манометра. Полученное значение занести в таблицу.
6. На короткое время соединить колбу с атмосферой, установив пневмотумблер «Атмосфера» в положение «Открыто».
7. Через 2–3 минуты, когда в колбе установится постоянное давление 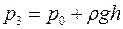 , определить разность уровней
, определить разность уровней 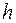 , установившуюся в манометре. Полученное значение занести в таблицу.
, установившуюся в манометре. Полученное значение занести в таблицу.
8. Повторить измерения пп. 2-6 не менее N=10 раз при различных значениях величины 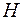 .
.
9. Выключить установку тумблером «Сеть».
§

