Примеры решения задач. задача 3.1.1вычислить массу и диаметр молекулы серебра, считая, что она имеет вид шарика и соприкасается с другими молекулами
ЗАДАЧА 3.1.1Вычислить массу и диаметр молекулы серебра, считая, что она имеет вид шарика и соприкасается с другими молекулами.
Дано: 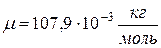 ;
; 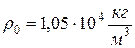 ;
; 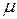 =107×10-3 кг/моль;
=107×10-3 кг/моль;
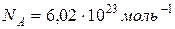 .
.
Найти: m0— ? d — ?
Решение
Определим массу молекулы серебра 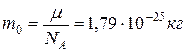 . Объем молекулы определим как объем шара
. Объем молекулы определим как объем шара 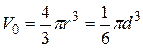 . Тогда диаметр молекулы серебра равен
. Тогда диаметр молекулы серебра равен 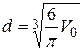 .
.
С другой стороны, выразим объём одной молекулы V0 через молярную массу 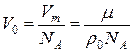 .
.
Подставим V0 в формулу для диаметра и получим 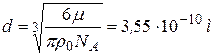 .
.
ЗАДАЧА 3.1.2Рассчитать среднюю длину свободного пробега молекул азота, коэффициент диффузии и вязкость при давлении 10 5 Па и температуре 17 0С. Как изменятся найденные величины в результате двукратного увеличения объёма газа: а) при постоянном давлении; б) при постоянной температуре? Эффективный диаметр молекул азота равен 3,7·10 –8см.
Дано: d = 3,7·10 –8см = 3,7·10 –10м; р = 105 Па.
Найти: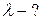 D — ?
D — ? 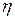 -?
-?
Решение
Средняя длина свободного пробега может быть рассчитана по формуле 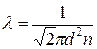 , где
, где 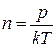 . Тогда
. Тогда 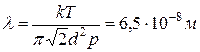 . Для расчёта коэффициента диффузии по формуле
. Для расчёта коэффициента диффузии по формуле 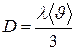 воспользуемся полученным результатом, определив предварительно среднюю арифметическую скорость
воспользуемся полученным результатом, определив предварительно среднюю арифметическую скорость 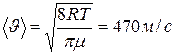 . Тогда
. Тогда
D = 1,0·10 –5м2/с. Коэффициент вязкости рассчитаем по формуле: 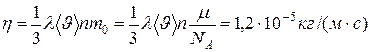 .
.
Как видно из формулы, средняя длина свободного пробега зависит только от концентрации молекул. При двукратном увеличении объёма концентрация уменьшается вдвое. Следовательно, при любом процессе 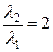 . Индексы 1 и 2 соответствуют состояниям до и после расширения газа.
. Индексы 1 и 2 соответствуют состояниям до и после расширения газа.
В выражение коэффициента диффузии входит не только длина свободного пробега, но и средняя скорость. Следовательно, 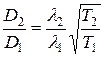 .
.
При постоянном давлении объём прямо пропорционален термодинамической температуре: 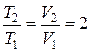 . Таким образом,
. Таким образом, 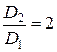
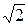 . Вязкость зависит только от скорости молекул, следовательно, и от температуры, т.е.
. Вязкость зависит только от скорости молекул, следовательно, и от температуры, т.е. 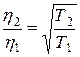 . Это значит, что при постоянном давлении
. Это значит, что при постоянном давлении 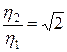 . При постоянной температуре коэффициент
. При постоянной температуре коэффициент 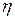 не изменяется.
не изменяется.
ЗАДАЧА 3.1.3Вычислить коэффициенты вязкости и диффузии кислорода, находящегося при давлении 0,2 МПа и при температуре 280 К. Диаметр молекулы принять равным 0,29 нм.
Дано: р = 0,2 МПа = 2∙105Па; m= 32∙10–3 кг/моль; d = 0,29нм = 2,9∙10–10м.
Т = 280 К.
Найти: 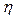 = ?
= ? 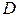 = ?
= ?
Решение.
Коэффициенты вязкости и диффузии равны соответственно
 , (8)
, (8) 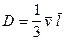 , (9)
, (9)
где 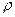 – плотность газа;
– плотность газа;
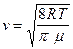 – средняя арифметическая скорость молекул; (10)
– средняя арифметическая скорость молекул; (10)
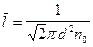 – длина свободного пробега молекул; (11)
– длина свободного пробега молекул; (11)
n0 – концентрация молекул.
Из соотношения р=nkT имеем 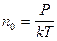 , где р – давление,
, где р – давление,
k – постоянная Больцмана.
Подставляя значение 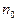 в (11), получим
в (11), получим
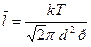 . (12)
. (12)
Определим численное значение коэффициента диффузии, подставляя (11) и (12) в (9):
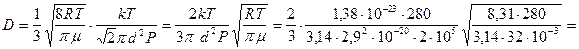
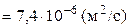 .
.
Чтобы найти коэффициент вязкости (1), определим плотность газа  , так как
, так как 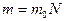 (масса 1-ой молекулы, N – число молекул);
(масса 1-ой молекулы, N – число молекул);
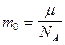 ,
, 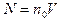 (где
(где 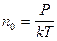 ),
), 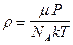 .
.
Из (1) и (2) следует, что 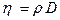 , то есть
, то есть
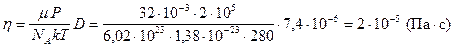 .
.
3.2 Задачи к теме « Физическая кинетика. Явления переноса»
177. Определить градиент плотности углекислого газа в почве, если через площадь в 1 м2 ее поверхности за 1 с в атмосферу прошел газ массой 8×10—8 кг. Коэффициент диффузии равен 0,04 см2/с.
178. Найти среднюю длину свободного пробега молекул азота при 0°С и при давлении 10— 3 мм рт.ст. Диаметр молекулы равен 0,3 нм.
179.Определить массу газа, продиффундировавшего за время 12 ч через поверхность почвы площадью 10 см2, если коэффициент диффузии 0,05 см2/с. Плотность газа на глубине 0,5 м равна 1,2×10—2 г/см3, а у поверхности 1,0×10—2 г/см3.
180. Найти число столкновений, испытываемых в течение 1 с молекулой гелия при нормальных условиях. Диаметр молекулы гелия считать равным 2·10-10 м.
181. Найти среднее число столкновений за 1 с и длину свободного пробега молекулы гелия, если газ находится под давлением 2 кПа при температуре 200 К. Эффективный диаметр молекулы 2×10-10 м.
182. Найти число столкновений в 1 с молекул некоторого газа, если длина свободного пробега при этих условиях равна 5×10-4 см и средняя квадратичная скорость 500 м/с.
183. Коэффициент диффузии водорода при нормальных условиях 0,91 см2/с. Определить коэффициент теплопроводности водорода.
184. Давление двухатомного газа вследствие сжатия увеличивается в 10 раз. Как и во сколько раз изменится длина свободного пробега молекул и коэффициент вязкости газа, если процесс: 1) изотермический;
2) адиабатический? Эффективный диаметр молекул считать
постоянным.
185. Оценить среднюю длину свободного пробега и время между двумя соударениями для протонов космических лучей в Галактике. Среднюю плотность межзвездного газа считать равной 104 частиц/см3, скорость протонов практически равна скорости света. Радиус протонов приблизительно равен 10-13 см.
186. Двухатомный газ адиабатически расширяется до объема в два раза большего первоначального. Как и во сколько раз изменятся коэффициенты теплопроводности и диффузии? Эффективный диаметр молекул считать постоянным.
187. Найти зависимость коэффициента теплопроводности от температуры при изохорическом процессе. Изобразить эту зависимость на графике.
188. Найти коэффициент внутреннего трения азота при нормальных условиях, если коэффициент диффузии для него при этих условиях равен D =0,142 см2/с.
189. Найти зависимость коэффициента теплопроводности от давления при изотермическом процессе. Построить график.
190. В сосуде объемом 0,5 л находится водород при нормальных условиях. Найти общее число столкновений между молекулами водорода в этом баллоне за 1с.
191. Определить, во сколько раз отличается коэффициент диффузии D1 газообразного водорода от коэффициента диффузии D2 газообразного кислорода, если оба газа находятся при одинаковых условиях.
192. Найти среднюю длину свободного пробега и среднее число столкновений молекул азота при нормальных условиях.
193. Найти зависимость коэффициент теплопроводности λ от температура при изобарическом процессе.
194. Найти число столкновений в 1 с молекул углекислого газа при температуре 1000 С, если средняя длина свободного пробега при этих условиях равна 8,7∙10-2 см.
195. Вычислить коэффициенты вязкости и диффузии кислорода, находящегося при давлении 0,2 МПа при температуре 300 К. Диаметр молекулы принять равным 0, 29 нм.
196. При нормальных условиях коэффициент внутреннего трения азота 0,017 мПа∙с. Найти среднюю длину свободного пробега.
197. Найти коэффициент вязкости, теплопроводности, диффузии кислорода при нормальных условиях. Диаметр молекулы кислорода принять равным 0,27 нм.
198. Найти число столкновений, испытываемых в течение 1с молекулой водорода при нормальных условиях. Диаметр молекулы считать равным 0,23 нм.
199. Найти число столкновений, испытываемых в течение 1с молекулой кислорода при нормальных условиях. Диаметр молекулы кислорода считать равным 0,27 нм.
200. Найти коэффициент диффузии и коэффициент внутреннего трения воздуха при нормальных условиях. Диаметр молекулы воздуха принять равным 0,3 нм, массу киломоля — 29 кг/моль.
201. Баллон объемом 5 л содержит водород массой 1г при температуре 170С. Определить среднее число соударений молекулы в секунду. Диаметр молекулы водорода принять равным 0,23 нм.
202. В баллоне, объем которого 2,53 л, содержится водород. Температура газа 1270С, давление 1000 мм рт.ст. Найти число молекул в баллоне и число столкновений, которые испытывает каждая молекула за 10 с. Диаметр молекулы водорода 0,23 нм.
203. Найти диаметр молекул газа, если для него при нормальных условиях длина свободного пробега молекул 112 нм. Какой это газ?
204. Определить концентрацию молекул водорода, если коэффициент диффузии водорода равен 1,4 см2/с, а коэффициент внутреннего трения 8,5×10-6 с/м2.
205. Найти среднюю длину свободного пробега молекул азота при 00С и при давлении 10 мм ртутного столба. Диаметр молекулы принять равным 0,3 нм.
206. Вычислить среднюю длину свободного пробега и время между двумя столкновениями молекул кислорода при давлении 1,510-6 мм рт. ст. и температуре 17 0 С. Диаметр молекулы кислорода принять равным 0,27 нм.
207. В баллоне, объем которого 2,53 л, содержится водород. Температура газа 1270С, давление 1000 мм рт. ст. Найти число молекул в баллоне и число столкновений, которые испытывает каждая молекула за 10 с. Диаметр молекулы водорода 0,23 нм.
208. Найти диаметр молекул водорода, если для водорода при нормальных условиях длина свободного пробега молекул 112 нм.
Date: 2022-07-17; view: 9958; Нарушение авторских прав
§
§
ЗАДАЧА 4.1.1 Водород, масса которого 6,5 г , находящийся при температуре 27° С, расширяется вдвое при р = const за счет притока тепла извне. Найти: 1) работу расширения; 2) изменение внутренней энергии;
3) количество теплоты, сообщенное газу.
Дано: 6,5 г=6,5∙10-3 кг; р = const; 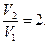
Найти: А-? DU-? Q-?
Решение
Приступая к решению задачи, прежде всего надо выявить характер процесса, протекающего в газе, и использовать соответствующие формулы (табл.1).
1. Вычислим значения молярных теплоемкостей водорода, учитывая, что молекулы водорода двухатомные и число степеней свободы i = 5:
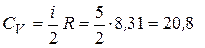 Дж/(моль К),
Дж/(моль К),
 .
.
2. Используя условие задачи и уравнение для изобарического процесса 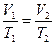 , найдем температуру газа после расширения:
, найдем температуру газа после расширения:
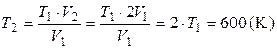 .
.
3. Вычислим изменение внутренней энергии и количество теплоты:
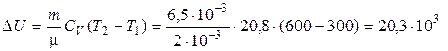 (Дж),
(Дж),
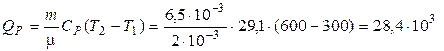 (Дж).
(Дж).
4. На основании первого начала термодинамики найдем работу расширения газа
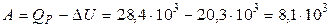 (Дж).
(Дж).
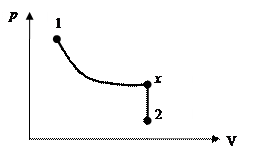
ЗАДАЧА 4.1.2 Двухатомный идеальный газ, занимающий при давлении
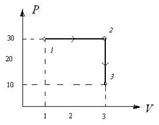
р1 = 3×105 Па объем V1= 4 л, расширяется до объема V2= 6 л, при этом давление падает до значения р2 = 105 Па. Процесс происходит сначала по адиабате, затем по изохоре (рисунок 12). Определить работу сил давления газа, изменение его внутренней энергии и количество поглощенной теплоты при этом переходе.
Дано: р1 = 3×105 Па ; р2 = 105 Па; V1= 4 л = 4 ×10 м-3; V2= 6 л=6 ×10 м-3 .
 Найти: А-? DU-? Q-?
Найти: А-? DU-? Q-?
Решение
1. Газ участвует в двух процессах: а) адиабатное расширение из состояния 1 в
некоторое состояние x, в котором объем
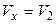 , (13)
, (13)
Рисунок 12
давление рx не известно;
б) изохорный процесс из состояния x в состояние 2. Найдем рx из уравнения адиабаты для двух состояний
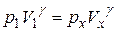 . (14)
. (14)
Для двухатомного газа i = 5, следовательно,
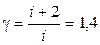 . (15)
. (15)
Значение рхполучим на основании (13), (14) и (15), а именно
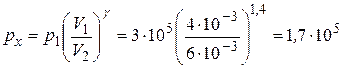 (Па).
(Па).
Откуда видим, что 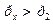 , и процесс 1-2 можно представить графически (рисунок 12).
, и процесс 1-2 можно представить графически (рисунок 12).
Учтем, что 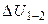 не зависит от вида процесса, а зависит только от начального и конечного состояний. Следовательно,
не зависит от вида процесса, а зависит только от начального и конечного состояний. Следовательно,
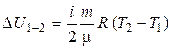 .
.
Из уравнения Клапейрона — Менделеева для состояний 1 и 2 имеем
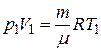 и
и 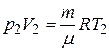 ,
,
откуда получим
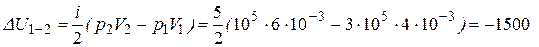 (Дж),
(Дж),
а это значит, что газ охлаждается.
2. Работу А1—2найдем как сумму работ: 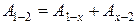 , где для изохоры х–2 Ах–2 = 0, для адиабаты 1–х:
, где для изохоры х–2 Ах–2 = 0, для адиабаты 1–х:
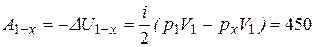 (Дж),
(Дж),
т.е. 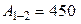 (Дж).
(Дж).
3. Количество теплоты Q1-2 складывается также как сумма теплот:  , где (табл.1) для адиабаты Q 1–x = 0, для изохоры х–2:
, где (табл.1) для адиабаты Q 1–x = 0, для изохоры х–2:
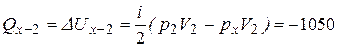 (Дж),
(Дж),
т.е. 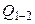 = – 1050 Дж, а это значит, что газ отдает тепло.
= – 1050 Дж, а это значит, что газ отдает тепло.
ЗАДАЧА 4.1.3При изобарическом расширении некоторой массы двухатомного газа, находящегося под давлением 105Па, его внутренняя энергия изменилась на 490 Дж. Найти приращение объема газа.
Дано: р=105 Па; DU=490 Дж; g = 1,4.
Найти: DV — ?
Решение
Чтобы определить приращение объема DV при изобарическом расширении, нужно знать работу, произведенную газом при этом процессе: 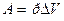 .
.
Работу можно вычислить и на основании первого начала термодинамики: 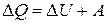 , откуда следует, что
, откуда следует, что 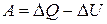 .
.
Количество тепла DQ, сообщенное при изобарическом расширении произвольной массе газа, равно:  .
.
Изменение внутренней энергии DU, которое произойдет при этом, 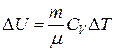 .
.
Разделив 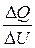 , получим:
, получим:  ,
, 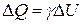 .
.
Подставим это значение в уравнение для работы:
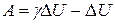 , или
, или 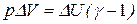 .
.
Отсюда найдем, что 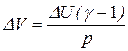 . DV = 1,96·10-3 м3.
. DV = 1,96·10-3 м3.
4 Задачи к теме «Физические основы термодинамики. Первое начало термодинамики»
209. Какова энергия поступательного и вращательного движения одной молекулы водорода при нормальных условиях (p = 1 атм, t = 0°C)?
210. Какова энергия поступательного и вращательного движения одной молекулы кислорода при нормальных условиях (p = 1 атм, t = 0°C)?
211.Какова энергия поступательного и вращательного движения одной молекулы азота при нормальных условиях (p = 1 атм, t = 0°C)?
212. Какова энергия поступательного и вращательного движения одной молекулы углекислого газа при нормальных условиях (p = 1 атм,
t = 0°C)?
213. Какова энергия поступательного и вращательного движения одной молекулы гелия при нормальных условиях (p = 1 атм, t = 0°C)?
214. Какова энергия поступательного и вращательного движения одной молекулы водяного пара при нормальных условиях (p = 1 атм,
t = 0°C)?
215. Какова среднеквадратичная скорость молекулы водорода при нормальных условиях (p = 1 атм, t = 0°C)? Найти вращательную энергию молекулы и атома водорода.
216. Какова среднеквадратичная скорость молекулы кислорода при нормальных условиях (p = 1 атм, t = 0°C)? Найти энергию поступательного и вращательного движений молекулы и атома кислорода при этих условиях.
217. Какова среднеквадратичная скорость молекулы углекислого газа при нормальных условиях ( p = 1 атм, t = 0°C)? Какова внутренняя энергия
1 г углекислого газа? Какова среднеквадратичная скорость молекулы гелия при нормальных условиях (p = 1 атм, t = 0°C)?
218. Какова среднеквадратичная скорость молекулы водяного пара при нормальных условиях (p = 1 атм, t = 0°C)? Найти энергию поступательного и вращательного движений молекулы гелия.
219. Какова внутренняя энергия одного моля водорода при нормальных условиях (p = 1 атм, t = 0°C)?
220. Какова внутренняя энергия одного моля кислорода при нормальных условиях (p = 1 атм, t = 0°C)? Какова среднеквадратичная скорость при этих условиях?
221. Какова внутренняя энергия одного моля азота при нормальных условиях (p = 1 атм, t = 0)? Какова среднеарифметическая скорость молекул азота при этих условиях?
222. Какова внутренняя энергия одного моля углекислого газа при нормальных условиях (p = 1 атм, t = 0°C)?
223. Какова внутренняя энергия одного моля гелия при нормальных условиях (p = 1 атм, t = 0°C)?
224. Какова внутренняя энергия одного моля водяного пара при нормальных условиях (p = 1 атм, t = 0°C)?
225. Какова внутренняя энергия одного грамма водорода при нормальных условиях (p = 1 атм, t = 0°C)?
226. Какова внутренняя энергия одного грамма кислорода при нормальных условиях (p = 1 атм, t = 0°C)?
227. Какова внутренняя энергия одного грамма азота при нормальных условиях (p = 1 атм, t = 0°C)?
228. Какова внутренняя энергия одного грамма углекислого газа при нормальных условиях (p = 1 атм, t = 0°C)?
229. Какова внутренняя энергия одного грамма гелия при нормальных условиях (p = 1 атм, t = 0°C)? Какова среднеквадратичная скорость молекул гелия при этих условиях?
230. Какова внутренняя энергия одного грамма водяного пара при нормальных условиях (p = 1 атм, t = 0°C)?
231. Какова концентрация кислорода при нормальных условиях (p = 1 атм, t =0°C)?
232. Какова удельная теплоемкость водорода при постоянном объеме?
233. Какова удельная теплоемкость кислорода при постоянном объеме?
234. Какова удельная теплоемкость азота при постоянном объеме?
235. Какова удельная теплоемкость углекислого газа при постоянном объеме?
236. Какова удельная теплоемкость гелия при постоянном объеме?
237. Какова удельная теплоемкость водяного пара при постоянном объеме?
238. Какова удельная теплоемкость водорода при постоянном давлении?
239. Какова удельная теплоемкость кислорода при постоянном давлении?
240. Какова удельная теплоемкость азота при постоянном давлении?
241. Какова удельная теплоемкость углекислого газа при постоянном давлении?
242. Какова удельная теплоемкость гелия при постоянном давлении?
243. Какова удельная теплоемкость водяного пара при постоянном давлении?
244. В запаянном баллоне объемом 4 л находится водород. При температуре 25°C его давление – 2 атм. Газ нагрели до температуры 250°C. Какое количество теплоты передано газу?
245. В запаянном баллоне объемом 4 л находится кислород. При температуре 25°C его давление – 2 атм. Газ нагрели до температуры 250°C. Какое количество теплоты передано газу?
246. В запаянном баллоне объемом 4 л находится азот. При температуре 25°C его давление – 2 атм. Газ нагрели до температуры 250°C. Какое количество теплоты передано газу?
247. В запаянном баллоне объемом 4 л находится углекислый газ. При температуре 25°C его давление – 2 атм. Газ нагрели до температуры 250°C. Какое количество теплоты передано газу?
248. В запаянном баллоне объемом 4 л находится гелий. При температуре 25°C его давление – 2 атм. Газ нагрели до температуры 250°C. Какое количество теплоты передано газу?
249. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится водород. Газ нагрели до температуры 250°C. Какое количество теплоты передано газу?
250. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится кислород. Газ нагрели до температуры 250°C. Какое количество теплоты передано газу?
251. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится азот. Газ нагрели до температуры 250°C. Какое количество теплоты передано газу?
252. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится углекислый газ. Газ нагрели до температуры 250°C. Какое количество теплоты передано газу?
253. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится гелий. Газ нагрели до температуры 250°C. Какое количество теплоты передано газу?
254. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится водород. Газ нагрели до температуры 250°C. Каков станет объем газа?
255. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится кислород. Газ нагрели до температуры 250°C. Каков станет объем газа?
256. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится азот. Газ нагрели до температуры 250°C. Каков станет объем газа?
257. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится углекислый газ. Газ нагрели до температуры 250°C. Каков станет объем газа?
258. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится гелий. Газ нагрели до температуры 250°C. Каков станет объем газа?
259. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится водород. Газ нагрели до температуры 250°C. Какую работу при этом совершит газ?
260. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится кислород. Газ нагрели до температуры 250°C. Какую работу при этом совершит газ?
261. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится азот. Газ нагрели до температуры 250°C. Какую работу при этом совершит газ?
262. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится углекислый газ. Газ нагрели до температуры 250°C. Какую работу при этом совершит газ?
263. В цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг при температуре 25°C находится гелий. Газ нагрели до температуры 250°C. Какую работу при этом совершит газ?
264. В теплоизолированном (при исходной температуре 25°C) цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг находится водород. На поршень поставили гирю массой 5 кг. Какая работа будет при этом совершена над газом?
265. В теплоизолированном (при исходной температуре 25°C) цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг находится кислород. На поршень поставили гирю массой 5 кг. Какая работа будет при этом совершена над газом?
266. В теплоизолированном (при исходной температуре 25°C) цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг находится азот. На поршень поставили гирю массой 5 кг. Какая работа будет при этом совершена над газом?
267. В теплоизолированном (при исходной температуре 25°C) цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг находится углекислый газ. На поршень поставили гирю массой 5 кг. Какая работа будет при этом совершена над газом?
268. В теплоизолированном (при исходной температуре 25°C) цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг находится гелий. На поршень поставили гирю массой 5 кг. Какая работа будет при этом совершена над газом?
269. В теплоизолированном (при исходной температуре 27°C) цилиндре объемом 3 л под поршнем площадью 20 см2 и массой 5 кг находится водород. На поршень поставили гирю массой 5 кг. На сколько возрастет при этом внутренняя энергия газа?
270. В теплоизолированном (при исходной температуре 25°C) цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг находится кислород. На поршень поставили гирю массой 5 кг. На сколько возрастет при этом внутренняя энергия газа?
271. В теплоизолированном (при исходной температуре 25°C) цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг находится азот. На поршень поставили гирю массой 5 кг. На сколько возрастет при этом внутренняя энергия газа?
272. В теплоизолированном (при исходной температуре 25°C) цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг находится углекислый газ. На поршень поставили гирю массой 5 кг. На сколько возрастет при этом внутренняя энергия газа?
273. В теплоизолированном (при исходной температуре 25°C) цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг находится гелий. На поршень поставили гирю массой 5 кг. На сколько возрастет при этом внутренняя энергия газа?
274. В теплоизолированном (при исходной температуре 25°C) цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг находится водород. На поршень поставили гирю массой 5 кг. На сколько уменьшится при этом потенциальная энергия поршня и гири?
275. В теплоизолированном (при исходной температуре 25°C) цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг находится кислород. На поршень поставили гирю массой 5 кг. На сколько уменьшится при этом потенциальная энергия поршня и гири?
276. В теплоизолированном (при исходной температуре 25°C) цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг находится азот. На поршень поставили гирю массой 5 кг. На сколько уменьшится при этом потенциальная энергия поршня и гири?
277. В теплоизолированном (при исходной температуре 25°C) цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг находится углекислый газ. На поршень поставили гирю массой 5 кг. На сколько уменьшится при этом потенциальная энергия поршня и гири?
278. В теплоизолированном (при исходной температуре 25°C) цилиндре объемом 4 л под поршнем площадью 20 см2 и массой 5 кг находится гелий. На поршень поставили гирю массой 5 кг. На сколько уменьшится при этом потенциальная энергия поршня и гири?
279. При выстреле вертикально вверх свинцовая пуля достигла высоты 1200 м. При падении, ударившись о землю, она нагрелась. Считая, что 50% механической энергии пули пошло на её нагревание, рассчитать, на сколько повысится её температура. Сопротивлением воздуха пренебречь.Удельная теплоемкость свинца 1,26·102 Дж/кг∙К.
280. Кислород O2 массой 6 г при температуре 30°C расширяется при постоянном давлении, увеличивая свой объем в два раза вследствие притока теплоты извне. Найти работу расширения, изменение внутренней энергии газа и количество теплоты, сообщенное кислороду.
281. Идеальная тепловая машина Карно, цикл которой совершается в обратном направлении (холодильная машина), использует воду при 0°C в качестве холодильника и воду при 100°C в качестве нагревателя. Сколько воды нужно заморозить в холодильнике, чтобы превратить в пар 500 г воды в кипятильнике?
282. Углекислый газ массой 10 г нагрет от 20 до 30°C при постоянном давлении. Найти работу расширения газа и изменение его внутренней энергии.
283. Какое количество теплоты потребуется для нагревания 0,5 кг вещества на 20С? Удельная теплоемкость вещества 70 Дж/(кг∙К).
284. Для изохорного нагревания идеального газа в количестве 800 моль на 500 К ему сообщили 9,4 МДж теплоты. Определить работу газа и изменение его внутренней энергии.
285. При сжатии одноатомного идеального газа его объем уменьшился в 6 раз, а давление возросло на 50%. Как изменилась внутренняя энергия газа?
286. Газ под давлением 0,2 МПа занимает объем 1 л. Определить кинетическую энергию поступательного движения всех молекул, находящихся в данном объеме.
287. Средняя квадратичная скорость поступательного движения молекул кислорода равна 1 км/с. Определить плотность кислорода, если он находится под давлением 0,3 МПа и среднюю кинетическую энергию одной молекулы.
288. В теплоизолированном цилиндре с поршнем находится азот массой 0,3 кг при температуре 200С. Азот, расширяясь, совершает работу 6705 Дж. Определить изменение внутренней энергии азота и его температуру после расширения.
289. Для изобарного нагревания идеального газа в количестве 800 моль на 500 К ему сообщили 9,4 МДж теплоты. Определить работу газа и изменение его внутренней энергии.
290. Найти среднюю кинетическую энергию вращательного движения одной молекулы водорода, а также суммарную кинетическую энергию всех молекул в одном моле водорода при температуре 190 К.
291. Вычислить энергию вращательного движения всех молекул водяного пара массой 36 г при температуре 20°С.
292. В сосуде находится газ, молярная масса которого 17×10—3 кг/моль. Отношение теплоемкостей газа Ср/Сv = 1,4. Вычислить удельные теплоемкости ср и сv.
293. Используя формулы молекулярно-кинетической теории, вычислить молярные и удельные теплоемкости аргона.
294.  Вода массой 200 кг с начальной температурой 20°С нагревается на 10°С. Определить энергию, затраченную на нагревание. Удельная теплоемкость воды 4200 Дж/(кг ∙ K). Ответ дать в МДж.
Вода массой 200 кг с начальной температурой 20°С нагревается на 10°С. Определить энергию, затраченную на нагревание. Удельная теплоемкость воды 4200 Дж/(кг ∙ K). Ответ дать в МДж.
295. На рисунке 13 представлены изменения давления и объема идеального одноатомного газа. Какое количество теплоты было получено или отдано газом при переходе из состояния 1 в состояние 3? Рисунок 13
296. На нагревание 1 кг воды с начальной температурой 20°С затратили 42 кДж энергии. Определить, на сколько градусов увеличилась температура воды? Удельная теплоемкость воды 4200 Дж/(кг ∙ K).
297. С какой высоты должен упасть кусок олова, чтобы при ударе о землю он расплавился? Начальная температура олова 0°С, на нагревание и плавление идет 50% работы силы тяжести. Удельная теплоемкость олова 250 Дж/кг∙K; температура плавления 232°С; удельная теплота плавления 5,8∙104 Дж/кг. Какова скорость его в момент удара о землю?
298. Идеальному одноатомному газу при изохорическом процессе сообщили 1000 Дж теплоты. Определить изменение внутренней энергии при этом процессе и работу газа.
299. Идеальный газ расширяется из объема V1 до объема V2 адиабатически и изотермически. При каком процессе произведена большая работа?
300. Теплоемкость газа зависит от вида процесса. В каких пределах она может изменяться и когда она наибольшая и когда наименьшая?
301. В сосуде, объем которого 5 л, находится кислород массой 4 г при температуре 13°С. Определить внутреннюю энергию газа и давление газа на стенки сосуда.
302. 12,5 г кислорода находятся в баллоне емкостью 0,01 м3. Какова средняя кинетическая энергия поступательного движения молекул газа и средняя квадратичная скорость их движения, если давление газа
1 атм.?
303. Найти среднюю кинетическую энергию вращательного движения одной молекулы водорода, а также суммарную кинетическую энергию всех молекул в одном моле водорода при температуре 190 К.
304. Средняя арифметическая скорость молекулы метана равна 600 м/с. Какова при этом энергия одного моля метана?
305. Средняя арифметическая скорость молекул азота при некоторой температуре равна 500 м/с. Найти внутреннюю энергию одного моля при этой температуре.
306. Газ занимает объем 1 л под давлением 0,2 МПа. Определить кинетическую энергию поступательного движения всех молекул, находящихся в данном объеме.
307. Определить среднюю кинетическую энергию вращательного движения одной молекулы двухатомного газа, если суммарная кинетическая энергия молекул одного киломоля этого газа 3,01 МДж.
308. Баллон содержит азот массой 2 кг при температуре 7°С. Определить кинетическую энергию поступательного движения и полную энергию молекул азота, находящегося в баллоне.
309. Определить энергию вращательного движения молекулы кислорода при температуре -173°С. Найти наиболее вероятную скорость молекул кислорода.
310. Вычислить среднюю энергию поступательного движения молекулы азота при температуре 137°С.
311. Вычислить энергию вращательного движения всех молекул водяного пара массой 36 г при температуре 20°С.
312. Определить полную кинетическую энергию молекул, содержащихся в киломоле азота при температуре 7°С.
313. Определить полную кинетическую энергию молекул углекислого газа массой 44 г при температуре 27°С.
314. Определить, во сколько раз показатель адиабаты для гелия больше, чем для углекислого газа.
315. Определить энергию поступательного движения молекул водяного пара массой 18 кг при температуре 16°С.
316. В сосуде находится газ, молярная масса которого 16×10-3 кг/моль. Отношение теплоемкостей газа Ср/Cv = 1,7. Вычислить удельные теплоемкости ср и сv.
317. Определить удельную теплоемкость при постоянном давлении смеси, состоящей из 1 кг гелия и 1 кг кислорода.
318. Найти отношение Ср/Cv для смеси газов, состоящей из 10 г гелия и
4 г водорода.
319. Вычислить молярные и удельные теплоемкости газа, если относительная молекулярная масса его равна 28, а отношение теплоемкостей Ср/Cv = 1,4.
320. Из баллона, содержащего водород под давлением 1 МПа при температуре 290 К, выпустили половину находящегося в нем газа. Считая процесс адиабатическим, определить конечную температуру и давление.
321. Используя формулы молекулярно-кинетической теории, вычислить молярные и удельные теплоемкости кислорода, озона.
322. Известны удельные теплоемкости ср = 912 Дж/(кг×К) и сv = 649 Дж/(кг×К). Определить молекулярный вес газа и число степеней свободы его молекул.
323. Найти количество теплоты, которое требуется сообщить смеси, состоящей из 0,5 кг кислорода и 1,5 кг азота, чтобы нагреть ее на 50°С при постоянном объеме.
324. Найти увеличение внутренней энергии гелия, изобарически расширявшегося от объема 5 л до объема 10 л. Процесс происходил при давлении 0,2 МПа.
325. Вычислить удельные теплоемкости при постоянном объеме сv и при постоянном давлении ср смеси неона и водорода. Массовые доли газов соответственно равны 0,4 и 0,6.
326. В цилиндре под поршнем находится водород массой 0,2 кг при температуре 20°С. Водород сначала расширился адиабатически, увеличив свой объем в 5 раз, а затем был сжат изотермически, причем объем уменьшился в 5 раз. Найти температуру в конце адиабатического расширения и полную работу, совершенную газом. Изобразить процесс графически в координатах р-V.
327. Одноатомный газ занимает объем 4 м3 и находится под давлением 0,8 МПа. После изотермического расширения этого газа установилось давление 105 Па. Определить: а) работу, совершенную газом при расширении; б) какое количество теплоты было поглощено газом в процессе расширения; в) как изменилась при этом внутренняя энергия газа.
328. Кислород массой 2 кг занимает объем 1 м3 и находится под давлением 0,2 МПа. При нагревании газ расширился при постоянном давлении до объема 3 м3, а затем его давление возросло до 0,5 МПа при неизменном объеме. Найти изменение внутренней энергии газа, совершенную им работу и теплоту, переданную газу. Построить график процесса в координатах р-V.
329. Два моля идеального двухатомного газа находятся под давлением p1=250 кПа и занимают объем V1=20 л. Сначала газ изохорически нагревают до температуры Т2=400 К. Далее, изотермически расширяя, доводят до первоначального давления. После этого путем изобарического сжатия возвращают газ в начальное состояние. Определить работу цикла и изменение внутренней энергии.
330. При адиабатическом расширении 1 кг воздуха его объем увеличился в 10 раз. Найти работу расширения, конечные давление и температуру, если начальное давление 1 атм, а начальная температура 15°С.
331. В четырехтактном двигателе дизеля засосанный атмосферный воздух в объеме 10 л подвергается 12-кратному сжатию. Предполагая процесс сжатия адиабатическим, определить конечное давление и температуру, если начальное давление и температура равны 1 атм и 10°С. Найти также работу сжатия.
332. В цилиндре под поршнем находится воздух, объем которого 500 см3 и давление 105 Па. Какую работу надо совершить, чтобы уменьшить объем газа вдвое? Рассмотреть два случая: 1) поршень при сжатии воздуха движется очень медленно; 2) поршень движется очень быстро.
333. Одному молю двухатомного газа сообщили 20 Дж тепла, в результате чего газ нагрелся на несколько градусов при постоянном объеме. Какое количество тепла надо сообщить 30 г метана, чтобы нагреть его на такое же число градусов при постоянном давлении?
334. 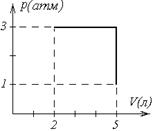 Некоторая масса азота переходит от первого состояния ко второму в два этапа: сначала по изохоре, затем по изобаре (рисунок 14). Определить изменение внутренней энергии, количество теплоты и произведенную работу.
Некоторая масса азота переходит от первого состояния ко второму в два этапа: сначала по изохоре, затем по изобаре (рисунок 14). Определить изменение внутренней энергии, количество теплоты и произведенную работу.
Рисунок 14
335.  В цилиндре под поршнем находится азот массой 20 г. Газ переведен из состояния 1 в состояние 2 в результате процесса, изображенного на диаграмме температура-давление (рисунок15). Определить теплоту, переданную газу, совершенную газом работу и приращение внутренней энергии. Рисунок 15
В цилиндре под поршнем находится азот массой 20 г. Газ переведен из состояния 1 в состояние 2 в результате процесса, изображенного на диаграмме температура-давление (рисунок15). Определить теплоту, переданную газу, совершенную газом работу и приращение внутренней энергии. Рисунок 15
336. Баллон с кислородом емкостью 20 л при давлении 100 атм и температуре 7°С нагревается до 27°С. Какое количество теплоты при этом поглощает газ, каково изменение внутренней энергии?
337. Во сколько раз увеличится объем водорода, взятого в количестве 0,4 моля, если при изотермическом расширении при температуре 27°С он получает 800 Дж тепла?
338. Углекислый газ, имеющий первоначальный объем 20 л и давление
1 атм., изотермически расширяется. Когда его объем становится 40 л, он продолжает расширяться при постоянном давлении до объема 60 л. Масса газа 44 г. Подсчитать общую работу газа за все время расширения и общее количество теплоты, полученное газом.
339. Воздух, находившийся под давлением p1 = 0,1 МПа, был адиабатически сжат до давления p2 = 1 МПа. Каково будет давление p3, когда сжатый воздух, сохраняя объем неизменным, охладится до первоначальной температуры? Воздух считать двухатомным газом. Изобразить эти процессы в координатах р-V.
340. В сосуде находится смесь азота с аммиаком. Средняя кинетическая энергия поступательного движения молекулы азота равна 0,63×10-20 Дж. Найти полную среднюю энергию молекулы аммиака.
341. Нагревается или охлаждается газ, если он расширяется по закону р×V2=const? Какова его молярная теплоемкость при этом процессе?
342. В вертикально расположенном цилиндре с площадью 1 дм2 под поршнем массой 10 кг, скользящим без трения, находится воздух. При изобарном нагревании воздуха поршень поднялся на 20 с. Какую работу совершил воздух, если наружное давление равно 100 кПа? Какое количество теплоты было при этом сообщено воздуху?
343. Найти среднюю кинетическую энергию поступательного и среднюю кинетическую энергию вращательного движения молекулы этана С2Н6 при температуре 270С. Молекулу считать жесткой.
344. Объем идеального газа увеличился от V1 до V2. Процесс расширения происходит: 1) изобарически; 2) изотермически; 3) адиабатически. Начертить графики этих процессов на диаграммах давление-объем и внутренняя энергия-объем. По графикам определить:
1)при каком процессе произведенная газом работа наименьшая;
2)знак приращения внутренней энергии при каждом процессе.
345. Коэффициент теплопроводности кислорода при некоторой температуре равен 0,0325 Вт/(м∙к). Найти коэффициент вязкости кислорода при этой температуре.
346. Внутренняя энергия трех киломолей трехатомного газа равна 9 МДж. Чему равна средняя кинетическая энергия вращательного движения молекулы этого газа?
347. Нагревается или охлаждается идеальный газ, если он расширяется по закону pV 1,4=const? Какова его молярная теплоемкость при этом процессе?
348. Средняя арифметическая скорость молекулы метана равна 600 м/с. Какова при этом энергия одного грамма и молекулы метана (СН4 )?
349. Масса смеси двух жидкостей 45 кг. Молярная теплоемкость первой жидкости равна 75,6 Дж/(К×моль), удельная теплоемкость второй равна 1 кДж/(К∙моль). Когда смеси сообщили 1134 кДж теплоты, она нагрелась на 100С. Найти массы первой и второй жидкостей. Масса моля первой жидкости 18 г/моль.
350. В баллоне находится аргон и азот. Определить удельную теплоемкость при постоянном давлении ср смеси, если массы их равны.
351. Водяной пар расширился при постоянном давлении. Определить работу расширения, если пару передано количество теплоты Q=12 кДж. (Пар считать идеальным газом).
352. Вычислить молярные и удельные теплоемкости для водорода и азота.
353. Определить среднее значение полной кинетической энергии одной молекулы и массы, равной m =1 кг гелия, кислорода, водяного пара при температуре 300 К.
354. Сравнить удельные теплоемкости при постоянном давлении и при постоянном объеме водорода с удельными теплоемкостями ср и сv кислорода.
355. Расширяясь, водород совершил работу А=36 кДж. Определить количество теплоты Q, подведенное к газу, если процесс протекал: 1)изобарически; 2) изотермически.
356. Смесь гелия и водорода находятся при температуре Т = 1200 К. Определить среднюю квадратичную скорость Vкв и среднюю кинетическую энергию молекул гелия и водорода.
357. Вычислить удельные теплоемкости при постоянном объеме сv и при постоянном давлении сp смеси неона и водорода. Массовые доли газов соответственно равны 0,6 и 0,4.
358. Сравнить молярные и удельные теплоемкости при постоянном давлении и при постоянном объеме водорода с молярной и удельной теплоемкостями при p = соnst и V = соnst окиси углерода.
359. Кислород, занимавший объем V = 2 л под давлением 1,2 МПа, адиабатически расширился до объема 20 л. Определить работу расширения.
360. Определить температуру Т газа, если средняя кинетическая энергия поступательного движения его молекул έ=1,6×10-19Дж.
361. Некоторая масса азота переходит от первого состояния ко второму в два этапа: сначала по изохоре, затем по изобаре. Определить изменение внутренней энергии, количество теплоты и произведенную работу.
362. Объем газа при адиабатическом сжатии уменьшился в 10 раз, а давление увеличилось в 21,4 раза. Определить отношение удельной теплоемкости при постоянном давлении к удельной теплоемкости при постоянном объеме для этого газа.
363. Какая доля внутренней энергии газообразного метана приходится на энергию вращательного движения?
364. Трехатомный газ совершает цикл, состоящий из четырех процессов. Вначале при постоянном объеме его давление возрастает втрое, после чего при постоянном давлении в пять раз возрастает объем. Затем происходит последовательно изохорический и адиабатический процессы, в результате которых газ возвращается в исходное состояние. Определить работу цикла и изобразить цикл в координатах р,V.
365. Производится сжатие некоторой массы двухатомного газа и в первом случае изотермически, во втором случае адиабатически. Начальные температура и давление сжимаемого газа в обоих случаях одинаковы. Конечное давление в n раз больше начального. Найти отношение работ при адиабатическом и изотермическом процессах при n = 2 и n = 100.
366. Баллон содержит водород массой 10 г при температуре 70С. Определить суммарную кинетическую энергию поступательного движения и полную кинетическую энергию всех молекул газа. Определить среднюю квадратичную и наиболее вероятную скорости водорода.
367. Удельная теплоемкость при постоянном объеме газовой смеси, состоящей из одного киломоля кислорода и нескольких киломолей аргона, равна 430 Дж/(кг∙К). Найти количество аргона.
368. Средняя арифметическая скорость молекул азота при некоторой температуре равна 500 м/с. Найти внутреннюю энергию одного моля азота при этой температуре.
369. Найти удельную теплоемкость при постоянном давлении газовой смеси, состоящей из 48 г озона и 4 г гелия
370. 200 г азота нагревается при постоянном давлении 200С до 1000С. Какое количество теплоты поглощается при этом? Каков рост внутренней энергии газа? Какую внешнюю работу производит газ?
371. В одном см3 содержится 1,45×1012 молекул, средняя кинетическая энергия которых при поступательном движении равна 1,242∙1020Дж. Определить давление, оказываемое газом на стенки сосуда,
372. Смесь газов состоит из 1 моля кислорода и двух молей углекислого газа. Какое количество теплоты потребуется, чтобы нагреть эту смесь от 200С до 500С?
373. Смесь аргона и гелия находится при температуре 12000С. Определить среднюю квадратичную скорость и среднюю кинетическую энергию поступательного движения атомов гелия и аргона.
374. Под действием высокой температуры 40% молекул водорода распались на атомы. Найти удельные теплоемкости ср и сv водорода при постоянном давлении и при постоянном объеме
375. Определить количество тепла, выделяющегося при изотермическом сжатии 7 г азота, находящихся при нормальных условиях, если конечное давление в 5 раз превышает первоначальное.
376. Водород, находившийся под давлением 0,1 МПа, был сжат адиабатически до давления 0,3 МПа. Чему будет равно давление, когда сжатый газ, не изменяя своего объема, охладится и примет первоначальную температуру? Начертить в координатах объем-давление графики имевших место процессов.
377. Определить среднее значение полной кинетической энергии одной молекулы гелия, кислорода, водяного пара при 400 К, а также их наиболее вероятные скорости.
378. Найти отношение Ср/Сv для смеси газов, состоящей из 20 г неона,
14 г азота и 15 г аммиака.
379. Один киломоль идеального двухатомного газа, находящийся под давлением в 1атм, при температуре 270С, нагревается при постоянном объеме до давления в 2 атм. После этого газ изотермически расширился до начального давления и затем изобарически снижается до начального объема. Начертить график цикла. Определить температуры газа для характерных точек цикла и работу цикла.
380. 22 г углекислого газа были нагреты на 500С при постоянном давлении. 4 г водорода были нагреты 200С при постоянном объеме. На нагрев какого газа было израсходовано больше теплоты? Во сколько раз больше?
381. В цилиндре под поршнем находится водород массой 0,02 кг при температуре 200С. Водород расширился адиабатически, увеличив свой объем в 5 раз. Найти температуру в конце адиабатического расширения в полную работу, совершенную газом. Изобразить процесс графически в координатах р-V.
382. Определить среднюю кинетическую энергию вращательного движения одной молекулы одноатомного газа, если суммарная кинетическая энергия молекул одного киломоля этого газа 3,01 МДж.
383. Найти количество теплоты, которое требуется сообщить смеси, состоящей из 0,5 кг азота и 0,4 кг кислорода, чтобы нагреть ее на 500С при постоянном объеме.
384. Смесь газов состоит из 1 кг водорода и 2 кг углекислого газа. Найти отношение энергии молекулы углекислого газа к энергии молекулы водорода. Найти также отношение общей энергии углекислого газа к общей энергии водорода.
385. Смесь состоит из двух молей гелия и одного моля азота. Определить удельные теплоемкости смеси при постоянном давлении и при постоянном объеме.
386. В бензиновом автомобильном моторе степень сжатия горячей смеси равна 6,2. Смесь засасывается в цилиндр при температуре 150 С. Найти температуру горячей смеси в конце такта сжатия. Горячую смесь рассматривать как двухатомный газ. Процесс считать адиабатическим.
387. Известны удельные теплоемкости газа сv = 649 Дж/(кг×К) и
ср = 912 Дж/(кг∙К). Определить молекулярный вес газа и число степеней свободы его молекул.
388. Определить удельную теплоемкость при постоянном давлении газовой смеси, состоящей из 1 кг гелия и 1 кг кислорода.
389. Двухатомный газ нагревают при постоянном объеме так, что его давление возрастает в 5 раз. Затем он изотермически расширяется, в результате чего его давление становится равным первоначальному. Найти отношение совершенной газом работы к полученному их количеству теплоты.
390. Найти полную кинетическую энергию, а также кинетическую энергию вращательного движения одной молекулы аммиака (NH3) при температуре 27 0С.
391. Найти отношение Ср/Сv для смеси газов, состоящей из 10 г гелия и
4 г водорода.
392. Некоторое количество азота находится при температуре 300 К и давлении 105 Па. Кинетическая энергия поступательного движения молекул равна 6,3 Дж. Найти число молекул газа, его массу и объем.
393. Разность удельных теплоемкостей при постоянном давлении и постоянном объеме двухатомного газа 297 Дж(кг×К). Определить удельные теплоемкости ср и сv газа.
394. Один киломоль двухатомного идеального газа совершает замкнутый цикл, график которого изображен на рисунке 2. Определить: 1) количество теплоты, полученное от нагревателя; 2) количество теплоты, переданное холодильнику; 3) работу, совершаемую газом за один цикл; 4) термический КПД цикла.
395. Один моль газа совершает цикл, состоящий из изохоры, изотермы и изобары. Определить температуры для характерных точек цикла и работу цикла, если V1=0,015м3, p1=105 Па, p2=3∙105 Па.
396. Углекислый газ, начальная температура которого 360 К, адиабатически снижается до 1/20 своего первоначального объема. Определить изменение внутренней энергии и совершенную при этом работу, если масса газа 20 граммов.
397. В сосуде, объем которого 5л, находится кислород массой 4 г при температуре 130С. Определить внутреннюю энергию газа и давление газа на стенки сосуда.
398. Вычислить молярные и удельные теплоемкости газа, если относительная молекулярная масса равно 44, а отношение теплоемкостей Ср/Сv = 1,4.
399. Кислород массой 2 кг занимает объем 1 м3 и находится под давлением 0,2 МПа. При нагревании газ расширился при постоянном давлении до объема 3 м3, а затем его давление возросло до 0,5 МПа при неизменном объеме. Найти изменение внутренней энергии газа, совершенную им работу и теплоту, переданную газу. Построить график процесса.
400. Найти полную кинетическую энергию, а также кинетическую энергию вращательного движения молекул аммиака (NН3) при температуре 270С.
401. Определить удельную теплоемкость при постоянном объеме газовой смеси, состоящей из 1 кг гелия и 1 кг кислорода.
402. При адиабатическом сжатии кислорода массой 1 кг, совершена работа 100 кДж. Какова конечная температура газа, если до сжатия кислород находился при температуре 300 К ?
403. При расширении кислорода объем его увеличился в 10 раз. В каком случае и во сколько раз совершенная при этом работа будет больше, если: 1) расширение адиабатическое; 2) расширение изотермическое?
404. Вычислить молярные и удельные теплоемкости газа, если относительная молекулярная масса его равна 30, а отношение теплоемкостей Ср/Сv =1,4.
405. Найти диаметр молекул водорода, если для водорода при нормальных условиях длина свободного пробега молекул 112 нм.
Date: 2022-07-17; view: 10989; Нарушение авторских прав
§
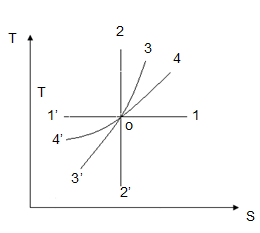
Рисунок 16
Таблица 2
| 0 – 1 Изотермическое расширение газа 0 – 1/ Изотермическое сжатие газа | dT = 0 dT = 0 | dS > 0 dS < 0 |
| 0 – 2 Адиабатическое сжатие 0 – 2/ Адиабатическое расширение | dT > 0 dT < 0 | dS = 0 dS = 0 |
| 0 – 3 Изохорическое нагревание 0 – 3/ Изохорическое охлаждение | dT > 0 dT < 0 | dS > 0 dS < 0 |
| 0 – 4 Изобарическое расширение 0 – 4/ Изобарическое сжатие | dT > 0 dT < 0 | dS > 0 dS < 0 |
Второе начало термодинамики может быть сформулировано как закон возрастания энтропии: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает 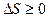 .
.
Второе начало термодинамики определяет направление протекания термодинамических процессов, указывая, какие процессы в природе возможны, а какие – нет.
Теорема Нернста(Третье начало термодинамики).
Энтропия любой термодинамической системы стремится к нулю при стремлении к нулю ее температуры
 .
.
Круговой процесс (цикл)
Круговой процесс (цикл)— процесс, при котором система, пройдя через ряд состояний, возвращается в исходное.
Коэффициент полезного действия(КПД) тепловой машины в общем случае
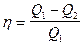 ,
,
где 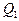 – количество теплоты, полученное рабочим телом от нагревателя;
– количество теплоты, полученное рабочим телом от нагревателя;
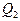 – количество теплоты, переданное рабочим телом охладителю.
– количество теплоты, переданное рабочим телом охладителю.
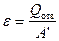 – холодильный коэффициент холодильной машины,
– холодильный коэффициент холодильной машины,
где 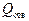 – теплота, отведенная от охлаждаемого тела;
– теплота, отведенная от охлаждаемого тела;
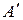 – работа, затраченная в цикле.
– работа, затраченная в цикле.
Date: 2022-07-17; view: 1394; Нарушение авторских прав
§
ЗАДАЧА 5.1.1 Кислород массой 0,2 кг нагревают от температуры 27° С до 127° С. Найти изменение энтропии, если известно, что начальное и конечное давление газа одинаковы.
Дано: 0,2 кг; 27° С ; 127° С; µ = 0,032 кг/моль.
Найти: DS -?
Решение
Энтропия является функцией состояния термодинамической системы, изменение которой в случае обратимого процесса равно приведенной теплоте процесса, т.е.
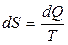
или в интегральной форме 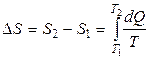 .
.
В нашем случае совершается обратимый изобарический процесс, для которого количество тепла при нагревании может быть найдено по формуле
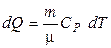 .
.
Подставляя 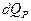 в подинтегральное выражение, получим
в подинтегральное выражение, получим
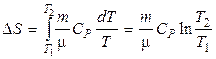 .
.
Используя формулу теплоемкости 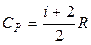 , где
, где  , получим
, получим
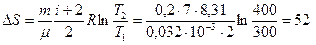 (Дж/К).
(Дж/К).
ЗАДАЧА 5.1.2Идеальная холодильная машина работает в интервале температур от 15 до –100С. Работа за один цикл равна 2·104 Дж. Вычислить количество теплоты, отданной теплоприемнику за один цикл, и холодильный коэффициент.
Дано: Т1= 150С = 288 К; Т2= -100С = 263 К; А = 2·104 Дж.
Найти: Q1 -? h2 -?
Решение
Идеальная холодильная машина работает по обратному циклу Карно. Расширение происходит при более низкой температуре Т2, чем сжатие Т1. КПД обратного и прямого циклов Карно одинаковы при работе с идеальным газом и равны
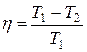 ;
; 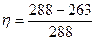 = 0,087.
= 0,087.
Количество теплоты, отданной теплоприемнику за один цикл,  , отсюда
, отсюда 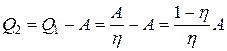 ;
;
Q2 = 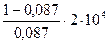 =2,1·105 Дж.
=2,1·105 Дж.
Q1 = 2,1·105 2·104 = 2,3·105 Дж.
Холодильная машина за каждый цикл будет передавать более горячему телу 2,3·105 Дж, из которых 2,0·104 Дж берется за счет превращения работы в теплоту, а остальные 2,1·105 Дж переносятся от холодного тела.
Холодильный коэффициент h2равен 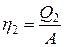 = 10,5.
= 10,5.
ЗАДАЧА 5.1.3Паровая машина мощность которой14,7 кВт потребляет за 1ч работы 8,1 кг угля с удельной теплотой сгорания 3,3·107 Дж/кг. Температура котла 200 0С, холодильника 58 0С. Найдите КПД этой машины и сравните его с кпд идеальной тепловой машины.
Дано: m = 8,1 кг; N = 14,7·10 3 Вт; q = 3,3·107 Дж/кг; Т1 = 473 К; Т2 = 331 К;
t = 1 ч = 3600 с.
Найти: 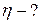
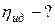

Решение
КПД тепловой машины равен отношению производимой механической работы А к затраченному количеству теплоты Q1, выделяющемуся при сгорании угля: 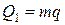 . Произведённая за это же время работа равна:
. Произведённая за это же время работа равна: 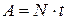 . Таким образом,
. Таким образом, 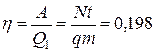 или
или 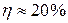 .
. 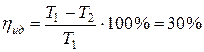 ,
, 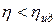 .
.
Коэффициент полезного действия идеальной тепловой машины больше КПД реальной машины.
ЗАДАЧА 5.1.4В ходе обратимого изотермического процесса, протекающего при температуре 350 К, тело совершило работу 80 Дж, а внутренняя энергия тела получила приращение 7,5 Дж. Найти приращение энтропии тела.
Дано: Т = 350 К; А = 80 Дж; 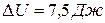 .
.
Найти: DS -?
Решение
Из первого начала термодинамики вытекает, что в ходе процесса тело получило количество теплоты: 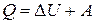 . С учётом того, что температура постоянна,
. С учётом того, что температура постоянна, 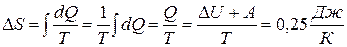 .
.
5.2 Задачи к теме «Второе начало термодинамики. Циклы. КПД циклов»
406. Некоторый тепловой двигатель на каждые 5 кДж тепла, полученные от нагревателя, производит 3 кДж работы. Сколько тепла он передает холодильнику? Каков КПД этого двигателя?
407. Некоторый тепловой двигатель на каждые 20 кДж тепла, полученные от нагревателя, производит 3 кДж работы. Сколько тепла он передает холодильнику? Каков КПД этого двигателя?
408. Некоторый тепловой двигатель на каждые 10 кДж тепла, полученные от нагревателя, производит 3 кДж работы. Сколько тепла он передает холодильнику? Каков КПД этого двигателя?
409.Некоторый тепловой двигатель на каждые 5 кДж тепла, полученные от нагревателя, производит 3 кДж работы. Температура нагревателя 1000°C. Какова максимально возможная температура холодильника?
410. Некоторый тепловой двигатель на каждые 20 кДж тепла, полученные от нагревателя, производит 3 кДж работы. Температура нагревателя 1000°C. Какова максимально возможная температура холодильника?
411. Некоторый тепловой двигатель на каждые 10 кДж тепла, полученные от нагревателя, производит 3 кДж работы. Температура нагревателя 1000°C. Какова максимально возможная температура холодильника?
412. Некоторый тепловой двигатель на каждые 5 кДж тепла, полученные от нагревателя, производит 3 кДж работы. Температура холодильника 25°C. Какова минимально возможная температура нагревателя?
413. Некоторый тепловой двигатель на каждые 20 кДж тепла, полученные от нагревателя, производит 3 кДж работы. Температура холодильника 25°C. Какова минимально возможная температура нагревателя?
414.Некоторый тепловой двигатель на каждые 10 кДж тепла, полученные от нагревателя, производит 3 кДж работы. Температура холодильника 25°C. Какова минимально возможная температура нагревателя?
415. Каков максимально возможный КПД теплового двигателя, работающего при температуре нагревателя 1000°C и температуре холодильника 200°C?
416. Каков максимально возможный КПД теплового двигателя, работающего при температуре нагревателя 1500°C и температуре холодильника 300°C?
417.Каков максимально возможный КПД теплового двигателя, работающего при температуре нагревателя 2000°C и температуре холодильника 500°C?
418.Каков максимально возможный КПД теплового двигателя, работающего при температуре помещения 25°C и температуре окружающей среды –30°C?
419. Каков максимально возможный КПД теплового двигателя, работающего при температуре помещения 20°C и температуре окружающей среды 0°C?
420. Каков максимально возможный КПД теплового двигателя, работающего при температуре помещения 25°C и температуре окружающей среды –10°C?
421. Каков максимально возможный КПД холодильника, работающего при температуре помещения 25°C и температуре морозильного отделения –30°C?
422. Каков максимально возможный КПД холодильника, работающего при температуре помещения 20°C и температуре морозильного отделения -100°C?
423. Найти работу тепловой машины за один цикл, изображенной на рисунке 23, и КПД цикла.
424. В идеальной тепловой машине количество теплоты, полученное от нагревателя, равно 6,3 кДж. 80% этой теплоты передаётся холодильнику. Найти КПД машины и работу за один цикл.
425. Газ в идеальной тепловой машине получает от нагревателя теплоту 42 кДж. Какую работу совершает газ, если абсолютная температура нагревателя в три раза выше, чем температура холодильника? Сколько тепла газ отдает холодильнику?
426. При совершении цикла Карно газ получил от нагревателя 16,8 кДж энергии и совершил 5,6 кДж работы. Во сколько раз температура нагревателя выше температуры холодильника?
427. Тепловая машина за цикл получает от нагревателя 200 Дж тепла и совершает полезную работу 60 Дж. Определить КПД этой машины.
428. Во сколько раз температура нагревателя больше температуры холодильника, если при цикле Карно с идеальным газом КПД составил 50%?
429. Идеальный газ в идеальной тепловой машине совершает цикл Карно, КПД которого 40% . На сколько процентов изменится КПД цикла Карно, если на 20% увеличить температуру нагревателя и на 10% уменьшить температуру охладителя?
430. Идеальная тепловая машина с КПД 60% за цикл работы получает от нагревателя 100 Дж. Какую полезную работу машина совершает за цикл?
431. Один киломоль идеального газа совершает цикл, состоящий из двух изохор и двух изобар. При этом объем газа изменяется от 25 м3 до 50 м3, а давление изменяется от 1 атм до 2 атм. Во сколько раз работа, совершаемая при таком цикле, меньше работы, совершаемой при цикле
Карно, изотермы которого соответствуют наибольшей и наименьшей температурам рассматриваемого цикла, если 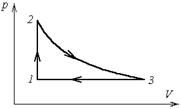 при изотермическом расширении объем увеличился в 2 раза?
при изотермическом расширении объем увеличился в 2 раза?
432. Один моль газа совершает цикл, состоящий из изохоры, изотермы и изобары (рисунок 21). Определить температуру для характерных точек цикла и работу цикла, если V1 =0,015 м3, p1 = 105 Па, p2 = 3×105 Па.
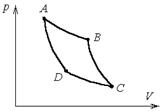 Рисунок 21
Рисунок 21
433. Двухатомный газ совершает цикл Карно, график которого изображен на рисунке 22. В состоянии В объем газа 12 л, давление 20 атм, а в состоянии С объем равен 16 л, давление 5 атм. Найти КПД цикла.
Рисунок 22
434. Вывести формулу для КПД цикла, состоящего из двух изобар и двух адиабат. Считать, что рабочее вещество является идеальным газом.
435. Газ, совершающий цикл Карно, получает от нагревателя 62 кДж теплоты. Какую работу совершает газ, если абсолютная температура нагревателя в два раза выше, чем температура холодильника?
436. 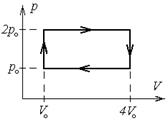 Двигатель работает как машина Карно и за цикл получает от нагревателя 3 кДж тепла. Температура нагревателя 600 К, температура холодильника 300 К. Найти совершаемую работу за цикл и количество теплоты, отдаваемое при этом холодильнику.
Двигатель работает как машина Карно и за цикл получает от нагревателя 3 кДж тепла. Температура нагревателя 600 К, температура холодильника 300 К. Найти совершаемую работу за цикл и количество теплоты, отдаваемое при этом холодильнику.
437. Идеальный многоатомный газ совершает цикл, изображенный на рисунке 23. Определить термический КПД цикла.
Рисунок 23
438. Совершая замкнутый цикл, газ получил от нагревателя 9,8 кДж теплоты. Термический КПД цикла равен 0,25. Какую работу совершил газ? Какое количество теплоты газ отдал холодильнику?
439. В сосуде содержится две различные молекулы. Каким числом способов могут быть распределены эти молекулы между левой и правой половинами сосуда? Используя формулу Больцмана, найти энтропию системы в случаях: 1) когда одна из половин сосуда пустая; 2) когда молекулы распределены в сосуде поровну.
440. В сосуде содержится два атома гелия и два атома неона. Каким числом способов могут быть распределены эти атомы между левой и правой половинами сосуда? Используя формулу Больцмана, найти энтропию в трех случаях: а) все атомы соберутся в одной половине; б) в одной находится 3, в другой 1; в) в обеих частях объема находятся по две частицы.
441. Как ведет себя энтропия термодинамической системы при адиабатическом процессе?
442. Азот массой 0,5 кг нагревают изохорически от температуры 27°С до 127°С. Найти изменение энтропии.
443. При температуре 0°С расплавили 1 кг льда. Найти изменение энтропии льда, если теплота плавления льда равна 3,33×105 Дж/кг.
444. Один киломоль кислорода расширился изотермически вдвое. Найти изменение энтропии при этом процессе.
445. Смесь водорода массой 0,02 кг и кислорода 0,32 кг нагревают при постоянном давлении от 27°С до 327°С. Найти изменение энтропии смеси.
446. Стальная гиря массой 2 кг вынута из холодильной камеры с температурой -73°С и внесена в помещение с температурой 27°С. Найти изменение энтропии гири, если теплоемкость стали 460 Дж/(кг×К).
447. В чайнике при нормальном давлении выкипел стакан воды (200 г). Найти изменение энтропии этой воды, если скрытая теплота парообразования воды равна 2,26×106 Дж/кг.
448. Два киломоля азота расширились изотермически втрое. Найти изменение энтропии при этом процессе.
449. КПД цикла Карно равен 0,3. При изотермическом расширении газ получил от нагревателя 200 Дж энергии. Определить работу, совершаемую при изотермическом сжатии.
450. Современный энергетический блок (паровой котел-турбина-генератор) мощностью 200 МВт потребляет в час 75 т угля с удельной теплотой сгорания 25 МДж/кг. Температура перегретого пара перед входом в турбину 5700 С, в конденсаторе 30 ºС. Найти фактический КПД энергетического блока и сравнить его КПД цикла Карно, осуществленного между такими же температурами.
451. Газ совершает цикл Карно. Абсолютная температура холодильника 290 К. Во сколько раз увеличится КПД, если температура нагревателя повысится от 400 К до 600 К?
452. Вывести формулу для КПД цикла, состоящего из двух изохор и двух адиабат. Считать, что рабочее вещество является идеальным газом.
453. Идеальный газ совершает цикл Карно. Температура Т1 нагревателя в три раза выше температуры Т2 охладителя. Нагреватель передал газу количество теплоты Q1=42 кДж. Какую работу совершил газ?
454. Идеальный газ, совершающий цикл Карно, получив от нагревателя количество теплоты Q1=804 кДж, совершил работу А=1180 Дж. Найти термический КПД этого цикла. Во сколько раз температура нагревателя больше температуры охладителя?
455. При совершении цикла Карно газ совершил работу 1 кДж и отдал холодильнику 4 кДж теплоты. Во сколько раз температура нагревателя больше температуры холодильника?
456.Газ, совершающий цикл Карно, отдал холодильнику 2/3 полученной от нагревателя теплоты. Определить работу изотермического сжатия газа, совершающего цикл Карно, если температуры нагревателя и холодильника 600К и 300К соответственно и газ получает от нагревателя за цикл 8 кДж теплоты.
457.Идеальная холодильная машина работает по обратному циклу Карно в интервале температур от 100 до 90 С. Работа машины за цикл
А=-1,55 кДж. Найти: 1) холодильный коэффициент; 2) количество тепла, отводимого от охлаждаемого тепла за цикл. Примечание. Холодильным коэффициентом называют отношение количества тепла, отводимого от охлаждаемого тела, к затраченной работе А =-А.
Date: 2022-07-17; view: 12323; Нарушение авторских прав
§
ЗАДАЧА 6.1.1 Найти эффективный диаметр молекулы азота, если для азота критическая температура –147,10С; критическое давление 3,5·105 Па.
Дано: tкр= –147,10С; ркр=33,5·105 Па.
Найти: s — ?
Решение
Постоянная b в уравнении Ван-дер-Ваальса приближенно равна учетверенному собственному объему молекул. Поэтому для одного моля газа имеем
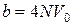 , (16)
, (16)
где N – число Авогадро;
V0 – объем одной молекулы, который равен 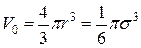 ,
,
где s —эффективный диаметр молекулы азота.
Подставляя значения V0 в (16), получим, что постоянная b равна 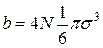 .
.
Откуда  .
.
Чтобы определить b, воспользуемся уравнениями, связывающими поправки Ван-дер-Ваальса с критической температурой и давлением
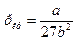 ;
; 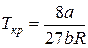 .
.
Решая эти уравнения относительно b, получим
.
Подставим значение b в уравнение для эффективного диаметра молекулы, получим
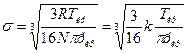 , (17)
, (17)
где 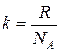 — постоянная Больцмана.
— постоянная Больцмана.
Подставляя численные значения в (17)в системе СИ, найдем
s » 3.12·10-10 м.
ЗАДАЧА 6.1.2.Моль кислорода расширяется адиабатически в пустоту, в результате чего объём газа увеличивается от 1 л до 10 л. Определить приращение температуры газа.
Дано:V1 = 1 л=10-3 м; V2 = 10 л= 10 -2м 3; а=0,136 Па·м6/моль2.
Найти: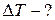
Решение
Расширяясь в пустоту, газ работы не совершает (А = 0). При адиабатическом процессе 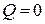 . Тогда согласно первому началу термодинамики
. Тогда согласно первому началу термодинамики 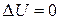 . Внутренняя энергия моля Ван-дер-Ваальсовского газа с двухатомными жёсткими молекулами определяется выражением:
. Внутренняя энергия моля Ван-дер-Ваальсовского газа с двухатомными жёсткими молекулами определяется выражением:
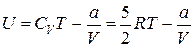 .
.
Приравнивая значения этого выражения для начального и конечного состояний газа, получим, что
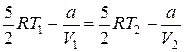 , откуда
, откуда 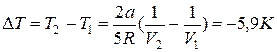 .
.
Газ охладился на 5,9 К.
6.2 Задачи к теме «Реальные газы»
458. Вычислить критическую температуру Ткр: 1) кислорода, 2) воды. Поправки Ван-дер-Ваальса:
1) для кислорода а = 0,136 Н×м4/моль2, в = 3,17×10-5 м3/моль;
2) для воды: а = 0,545 Н×м4/моль2, в = 3,04×10-5 м3/моль.
459. Найти критический объем Vкр кислорода массой m=0,5 кг. Поправки
Ван-дер-Ваальса: для кислорода а=0,163 Н∙м4/моль2, в=3,17∙10-5 м3/моль.
460. В баллоне емкостью 4 л находится кислород массой m=0,15 кг при температуре 300К. Определить отношение внутреннего давления р1 к давлению газа р на стенки сосуда. Поправки Ван-дер-Ваальса:
а=0,136 Н∙м4/моль2, в=3,04∙10-5 м3/моль.
461. В баллоне емкостью V=8 л находится кислород массой 3 кг при температуре Т=300 К. Найти, какую часть емкости занимает собственный объем молекул газа. Поправки Ван-дер-Ваальса:
а=0,136 Н∙м4/моль2, в=3,17∙10-5м3/моль.
462. Вычислить критическое давление Ркр : 1) кислорода; 2) воды. Поправки Ван-дер-Ваальса:
1) для кислорода: а=0,136 Н· м 4 /моль2, в=3,17· 10-5 м3 /моль;
2) для воды: а=0,545 Н·м4 /моль2, в=3,04·10-5 м3/моль.
463. В сосуде вместимостью V=10 л находится азот массой = 0,156 кг. Определить: 1) внутреннее давление р1’ газа; 2) собственный объем V1молекул. Рассматривать как идеальный газ. Поправки Ван-дер-Ваальса: а=0,135 Н∙м4/моль2, в=3,86∙10-5 м3/моль.
464. Доказать, что теплоемкость Cv газа, подчиняющего уравнению Ван-дер-Ваальса, не зависит от объема, а является функцией только температуры. Найти выражение для внутренней энергии газа Ван-дер-Ваальса, теплоемкость которого не зависит от температуры.
465. Моль азота расширяется в пустоту от начального объема 1 л до конечного 10 л.Найти понижение температуры Т при таком процессе, если постоянная a в уравнении Ван-дер-Ваальса для азота равна
1,36∙106 атм∙см6 / моль2.
466. Азот при критической температуре Tкр=147°С имеет критический объем Vкр=0,12 л/моль. Считая, что азот подчиняется уравнению Ван-дер-Ваальса, найти понижение температуры 7г азота при расширении в пустоту объема V1=5 л до объема V2 =50 л.
467. Моль кислорода расширяется адиабатический в пустоту, в результате чего объём газа увеличивается от 1 л до 10 л. Определить приращение температуры газа.
468. Объем 1г азота увеличивается от 1 л до 5 л. Рассматривая газ как реальный, найти работу внутренних сил при этом расширении.
469. В баллоне емкостью 8 л находится 0,3 кг кислорода при температуре 27˚С. Определить: какую часть объема сосуда составляет собственный объем молекул; какую часть давления газа на стенки сосуда составляет внутреннее давление, обусловленное силами притяжений молекул.
470. Как изменилось бы давление газа в сосуде, если бы внезапно силы притяжения между молекулами исчезли при неизменной температуре?
471. Какое количество тепла надо подвести к одному молю газа Ван-дер-Ваальса, чтобы при расширении в пустоту от объема V1 до объема V2 его температура не изменилась?
472. Найти эффективный диаметр молекулы азота, если для азота критическая температура -147,1 0С, критическое давления 33,5∙105 Па.
473. Найти постоянные уравнения Ван-дер-Ваальса для азота, если tкр азота равна -146˚С , pкр=33 атм.
474. Найти критическую плотность воды, если критическое давление для воды ркр=195 атм, а критическая температура Tкр=374˚С, предполагая, что вода подчиняется уравнению Ван-дер-Ваальса.
475. Принимая постоянную a Ван-дер-Ваальса для воды равной 5,47∙106атм∙см6/моль2, найти внутреннее давление воды p.
476. Имеется три непрозрачных цилиндра, закрытых подвижными поршнями. Известно, что в первом цилиндре находится газ при температуре выше критической, во втором – насыщенный пар, а в третьем ненасыщенный пар. Как определить, что находится в каждом из цилиндров?
477. Моль азота охлаждается до -100 ˚С. Определить давление, оказываемое газом на стенки сосуда, если занимаемый газом объем 0,100 л. Сравнить p с pид , которое имел бы азот, если бы сохранил при рассматриваемых условиях свойства идеального газа.
478. Два сосуда с объемами V1 и V2 соединены трубкой с краном. В каждом из них при закрытом кране находится по одному молю одного и того же газа, подчиняющегося уравнению Ван-дер-Ваальса. До открытия крана температура газа в обоих сосудах была одинакова и равна T . Нагреется или охладится газ, если открыть кран? На сколько при этом изменится температура газа? Определить давление газа после открытия крана. Стенки сосуда и соединяющей их трубки считать адиабатическими, а теплоемкость Cv – не зависящей от температуры.
479. Два баллона с объемами V1=V2=V=1 л соединены трубкой с краном. В объеме V1 находится воздух под атмосферным давлением, а объем V2 откачен до предельного вакуума. Считая, что воздух подчиняется уравнению Ван-дер-Ваальса, а стенки баллонов и трубки адиабатические, определить, на сколько изменится температура газа после открытия крана. Начальная температура T=290 K, для воздуха a=1,39·106 атм·см6/моль2.
480. Критическая температура углекислого газа СО2 равна 31˚С, критическое давление 73 атм. Определить критический объем Vкр моля СО2.
481. Поправки для воды в уравнении Ван-дер-Ваальса равны
a=0,566 H×м4/моль2, b=3,06×10-5 м3/моль. Определить критический объем для 1 кг воды.
482. Найти критические параметры неона, если его постоянные в уравнении Ван-дер-Ваальса a=0,209 H×м4/моль2, b=1,7×10-5м3/моль.
483. Азот массой 14 кг занимает объем 0,5 м3 при температуре 0˚С. Пользуясь уравнением Ван-дер-Ваальса, найти, на сколько нужно изменить температуру газа, чтобы его давление увеличилось вдвое.
484. В сосуде, объем которого 10 л, находится 360 г водяного пара при температуре 470 К. Вычислить давление пара, используя уравнение Ван-дер-Ваальса.
485. Определить эффективный диаметр молекулы газа, для которого критическая температура равна 282,7 К, поправка в уравнении Ван-дер-Ваальса: a=45,3×10-2 H×м4/моль2.
486. По уравнению Ван-дер-Ваальса определить давление, под которым находится 1 моль азота в сосуде объемом 2,5 м3, если его температура 310 К.
487. Найти постоянные в уравнении Ван-дер-Ваальса для углекислого газа, если критическая температура 304 К, а критическое давление 7370 кПа.
Date: 2022-07-17; view: 7057; Нарушение авторских прав
§
Изучение явления переноса (примеры решения задач). первое начало термодинамики, страница 11
3.
Найти коэффициент
внутреннего трения азота при нормальных условиях, если коэффициент диффузии для
него в этих условиях равен
0,142 см2/с.
4.
Найти диаметр
молекулы кислорода, если известно, что для кислорода коэффициент внутреннего
трения при 0 ºС равен η =18,8∙10–6 Н∙с/м2.
5.
Коэффициенты
диффузии и внутреннего трения равны соответственно 1,22∙105 м2/с
и η = 1,95∙10–5 кг/м∙с. Найти в этих условиях: а) плотность
кислорода, б) среднюю длину свободного пробега его молекул, в) среднюю
арифметическую скорость его молекул.
6.
Какой наибольшей
скорости может достичь дождевая капля диаметром 0,3 мм? Диаметр молекулы воздуха принять равным 3∙10–10 м,
температуру воздуха 0ºС. Считать, что для дождевой капли справедлив закон Стокса.
7.
Пространство
между двумя коаксиальными цилиндрами заполнено газом. Радиусы цилиндров равны
соответственно r = 5 см, R = 5,2 см. Высота внутреннего цилиндра равна h =
25 см. Внешний цилиндр вращается со скоростью, соответствующей n = 360 оборотов в минуту. Чтобы внутренний
цилиндр оставался неподвижным, к нему надо приложить касательную силу
F = 1,38∙103 Н. Рассматривая
в первом приближении случай как плоский, определить из данных этого опыта
коэффициент вязкости газа, находящегося между цилиндрами.
8.
Расстояние между
стенками дюаровского сосуда равно 8 мм. При каком давлении теплопроводность
воздуха, находящегося между стенками сосуда, начинает уменьшаться при откачке?
Температура воздуха 17ºС, диаметр молекул воздуха принять равным 3∙10–7 мм.
9.
Между двумя
пластинами, находящимися на расстоянии 1 мм друг от друга, находится воздух. Между пластинами поддерживается разность температур ΔT = 1 К. Площадь каждой пластины равна S = 100 см2. Какое количество
тепла передается за счет теплопроводности от одной пластины к другой за 10 мин?
Считать, что воздух находится при нормальных условиях. Диаметр молекулы принять
равным 3∙10–10 м.
10.
Самолет летит со
скоростью 360 км/ч. Считая, что слой воздуха у крыла самолета, увлекаемый
вследствие вязкости, равен 4 см, найти касательную силу, действующую на каждый
квадратный метр поверхности крыла. Диаметр молекулы воздуха принять равным 3∙10–8 см. Температура
воздуха 0ºС.
11.
Какой толщины
следует сделать деревянную стену здания, чтобы она давала такую же потерю
теплоты, как кирпичная стена толщиной d = 40 см при одинаковой температуре внутри и снаружи
здания. Коэффициенты теплопроводности кирпича и дерева соответственно равны ![]() = 0,7 Вт/(м∙К),
= 0,7 Вт/(м∙К), ![]() = 0,175 Вт/(м∙К).
= 0,175 Вт/(м∙К).
12.
Для расчета
отопительной системы необходимо найти потерю теплоты одного метра стены здания
в течение суток. Толщина стены d = 50 см, температура стены внутри и снаружи здания соответственно равна t1 = 18 ºC и
t2 = –30 ºC, коэффициент теплопроводности стены ![]() =
=
0,2 Вт/(м∙К).
13.
Стальная стенка
котла толщиной d1 = 1,5 мм покрыта с внутренней стороны слоем котельной накипи толщиной d2 = 1 мм. Определить тепловой поток, проходящий через 1 м2 стенки котла и температуру
стального листа над накипью, если температура наружной поверхности стенки t1 = 250 ºС и внутренней t2 = 200 ºC. Коэффициент теплопроводности стали и накипи соответственно ![]() = 45 Вт/(м∙К),
= 45 Вт/(м∙К), ![]() = 0,6 Вт/(м∙К).
= 0,6 Вт/(м∙К).
14.
Определить время
подъема движущихся с постоянной скоростью пузырьков воздуха со дна водоема
глубиной h = 1 м, если диаметры пузырьков соответственно равны 2 мм и 1 мм. Расширением пузырьков пренебречь.
§
ЗАДАЧА 1. В топке
парового котла сжигается ![]() кг топлива в час
кг топлива в час
с теплотой сгорания ![]() МДж/кг. Определить потерю
МДж/кг. Определить потерю
теплоты ![]() стенами топки в окружающую среду в
стенами топки в окружающую среду в
процентах от общего количества выделяемого тепла, если поверхность стен топки ![]() м2, толщина стен
м2, толщина стен ![]() мм, теплопроводность кладки
мм, теплопроводность кладки ![]() , а температура с внутренней и наружной
, а температура с внутренней и наружной
сторон соответственно равна ![]() и
и ![]() .
.
АНАЛИЗ. Потеря тепла
происходит за счет теплопроводности стен топки. Для определения ![]() количества тепла, переданного стеной
количества тепла, переданного стеной
окружающей среде за время ![]() , следует
, следует
использовать уравнение теплового потока: ![]() .
.
Полное количество тепла ![]() , выделенное в потоке
, выделенное в потоке
за время ![]() определится из равенства
определится из равенства ![]() . Величина потери теплоты
. Величина потери теплоты ![]() стенами топки в окружающую среду в
стенами топки в окружающую среду в
процентах запишется в виде: 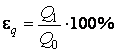 .
.
РЕШЕНИЕ. Воспользуемся
уравнением теплового потока и найдём количество тепла ![]() ,
,
переданного стенами топки (поверхностью S) за время ![]() :
:
![]() .
.
Учтем, что расстояние
между плоскостями ![]() , а разность температур
, а разность температур ![]() . Найдём, что
. Найдём, что ![]() ,
,
т.к. по условию задачи ![]() . В результате получим
. В результате получим ![]() . Потерю теплоты стенами топки в
. Потерю теплоты стенами топки в
окружающую среду в процентах от общего количества тепла ![]() определим
определим
по формуле: 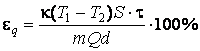 .
.
Проверим полученную формулу
на размерность:
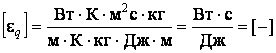 .
.
Подставим численные
значения:
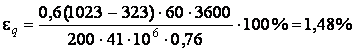 .
.
ОТВЕТ: 1,48 %.
ЗАДАЧА 2. Определить
тепловой поток через огнеупорную обмуровку теплового агрегата, если толщина
обмуровки равна 400 мм, температура поверхностей обмуровки: ![]() и
и ![]() ,
,
а коэффициент теплопроводности огнеупора изменяется по закону: ![]() , где
, где ![]() ,
,
![]() . Температура приведена в градусах
. Температура приведена в градусах
Цельсия.
§
АНАЛИЗ. При решении задачи
следует воспользоваться уравнением теплового потока ![]() ,
,
учитывая, что коэффициент теплопроводности ![]() изменяется
изменяется
с температурой по закону: ![]() (рис. 1.2.1),
(рис. 1.2.1),
где t – температура в градусах Цельсия.
РЕШЕНИЕ. Запишем
уравнение Фурье в виде ![]() , где под dx
, где под dx
будем понимать бесконечно тонкий слой обмуровки, в пределах которого коэффициент
теплопроводности и температура t постоянны. Подставив значение ![]() , получим
, получим ![]() .
.
Разделим переменные этого дифференциального уравнения, а затем проинтегрируем:
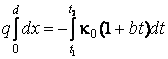 ,
,
следовательно, тепловой поток ![]() определится из равенства:
определится из равенства:
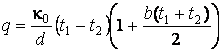 .
.
Проверим формулу на
размерность: 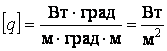 .
.
Подставим численные
значения:
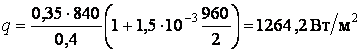 .
.
ОТВЕТ: ![]() .
.
ЗАДАЧА 3.При
определении вязкости жидкостей по методу Стокса расчёты ведут в предположении,
что скорость падения шарика постоянна и равна его скорости при установившемся
режиме движения: ![]() . В какой степени верно это
. В какой степени верно это
предположение? Через какой промежуток времени скорость шарика станет равной ![]() , если плотность материала шарика
, если плотность материала шарика ![]() , его диаметр
, его диаметр ![]() ,
,
динамическая вязкость жидкости ![]() ? В начальный
? В начальный
момент времени скорость шарика ![]() .
.
АНАЛИЗ. При решении задачи будем
использовать закон Стокса для расчёта силы сопротивления движению шарика в
жидкости: ![]() , где r – радиус шарика,
, где r – радиус шарика, ![]() – вязкость жидкости,
– вязкость жидкости, ![]() – скорость шарика.
– скорость шарика.
РЕШЕНИЕ. Составим
дифференциальное уравнение движения шарика массы m: ![]() . В проекции на ось OY (рис
. В проекции на ось OY (рис
1.2.2.) получим:
![]() ,
,
(1.2.1.)
где r2 –
плотность жидкости.
Решим дифференциальное уравнение
(1.2.1) методом разделения переменных и найдём время t, по истечении
которого скорость шарика станет равной некоторому значению ![]() . Для этого обозначим величину
. Для этого обозначим величину ![]() , коэффициент перед переменной
, коэффициент перед переменной ![]() через
через ![]() .
.
Учтём, что ![]() , где
, где ![]() –
–
объём шарика. Следовательно,![]() , а
, а 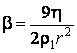 .
.
